4.26: Scatterplots (3 of 5)
- Page ID
- 251312
Learning Objectives
- Use a scatterplot to display the relationship between two quantitative variables. Describe the overall pattern (form, direction, and strength) and striking deviations from the pattern.
Now we return to our previous example. We apply the ideas of direction, form, and strength to describe the relationship between the age of the driver and the maximum distance to read a highway sign. Here is the scatterplot:
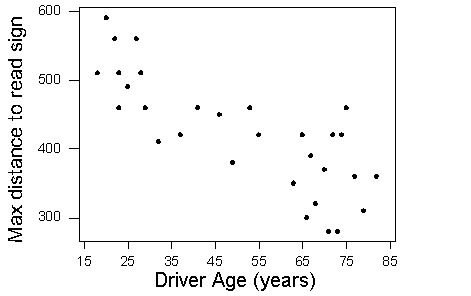
Direction: The direction of the relationship is negative. An increase in age is associated with a decrease in reading distance, which makes sense because older drivers tend to have diminished eyesight. So most older drivers can read the sign only when they are close to it. In other words, they have a shorter maximum reading distance.
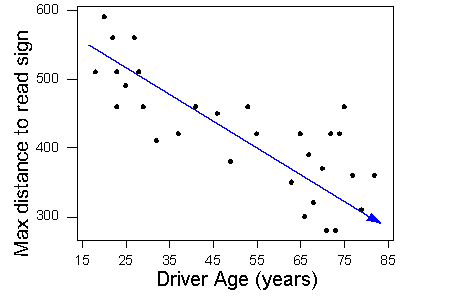
Form: The form of the relationship is linear.
Strength: The data points are fairly close to the line, so the relationship is moderately strong. Do not worry if you feel uncertain about describing the strength of a relationship. We mentioned earlier that descriptions of strength are not very precise. We develop a more precise measure of the strength shortly.
Outliers: There are no outliers. All the data points tend to follow the linear pattern.
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution

