2.12: Sampling (1 of 2)
- Page ID
- 251273
Learning Objectives
- For an observational study, critique the sampling plan. Recognize implications and limitations of the plan.
We now focus on observational studies and how to collect reliable and accurate data for an observational study.
We know that an observational study can answer questions about a population. But populations are generally large groups, so we cannot gather data from every individual in the population. Instead, we select a sample and gather data from the sample. We use the data from the sample to make statements about the population.
Here are two examples:
- A political scientist wants to know what percentage of college students consider themselves conservatives. The population is college students. It would be too time consuming and expensive to poll every college student, so the political scientist selects a sample of college students. Of course, the sample must be carefully selected to represent the political perspectives that are present in the population.
- A government agency plans to test airbags from Honda to determine if the airbags work properly. Testing an airbag means it has to be inflated and punctured, which ruins the airbag, so the researchers certainly cannot test every airbag. Instead, they test a sample of airbags and draw a conclusion about the quality of airbags from Honda.
Important Point
Our goal is to use a sample to make valid conclusions about a population. Therefore, the sample must be representative of the population. A representative sample is a subset of the population that reflects the characteristics of the population.
A sampling plan describes exactly how we will choose the sample. A sampling plan is biased if it systematically favors certain outcomes.
In our discussion of sampling plans, we focus on surveys. The next example is a famous one that illustrates how biased sampling in a survey leads to misleading conclusions about the population.
Example
The 1936 Presidential Election
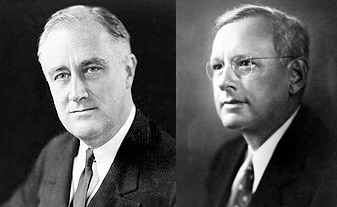
In 1936, Democrat Franklin Roosevelt and Republican Alf Landon were running for president. Before the election, the magazine Literary Digest sent a survey to 10 million Americans to determine how they would vote. More than 2 million people responded to the poll; 60% supported Landon. The magazine published the findings and predicted that Landon would win the election. However, Roosevelt defeated Landon in one of the largest landslide presidential elections ever.
What happened?
The magazine used a biased sampling plan. They selected the sample using magazine subscriptions, lists of registered car owners, and telephone directories. The sample was not representative of the American public. In the 1930s, Democrats were much less likely to own a car or have a telephone. The sample therefore systematically underrepresented Democrats. The poll results did not represent the way people in the general population voted.
Before we discuss a method for avoiding bias, let’s look at some examples of common survey plans that produce unreliable and potentially biased results.
Example
How to Sample Badly
Online polls: The American Family Association (AFA) is a conservative Christian group that opposes same-sex marriage. In 2004, the AFA began a campaign in support of a constitutional amendment to define marriage as strictly between a man and a woman. The group posted a poll on its website asking AFA members to voice their opinion about same-sex marriage. The AFA planned to forward the results to Congress as evidence of America’s opposition to same-sex marriage. Almost 850,000 people responded to the poll. In the poll, 60% favored legalizing same-sex marriage.
What happened? Against the wishes of the AFA, the link to the poll appeared in blogs, social-networking sites, and a variety of email lists connected to gay/lesbian/bisexual groups. The AFA claimed that gay rights groups had skewed its poll. Of course, the results of the poll would have been skewed in the other direction had only AFA members been allowed to participate.
This is an example of a voluntary response sample. The people in a voluntary response sample are self-selected, not chosen. For this reason, a voluntary response sample is biased because only people with strong opinions make the effort to participate.
Mall surveys: Have you ever noticed someone surveying people at a mall? People shopping at a mall are more likely to be teenagers, retired people, or people who have more money than the typical American. In addition, unless interviewers are carefully trained, they tend to interview people with whom they are comfortable talking. For these reasons, mall surveys frequently overrepresent the opinions of white middle-class or retired people. Mall surveys are an example of a convenience sample.
Example
How to Eliminate Bias in Sampling
In a voluntary response sample, people choose whether to respond. In a convenience sample, the interviewer chooses who will be part of the sample. In both cases, personal choice produces a biased sample. Random sampling is the best way to eliminate bias. Collecting a random sample is like pulling names from a hat (assuming every individual in the population has a name in the hat!). In a simple random sample everyone in the population has an equal chance of being chosen.
Reputable polling firms use techniques that are more complicated than pulling names out of a hat. But the goal is the same: eliminate bias by using random chance to decide who is in the sample.
Random samples will eliminate bias, even bias that may be hidden or unknown. The next three activities will reveal a bias that most of us have but don’t know that we have! We will see how random sampling avoids this bias.
Random Samples
Instructions: Use the simulation below for this activity. You will see 60 circles. This is the “population.” Our goal is to estimate the average diameter of these 60 circles by choosing a sample.
- Choose a sample of five circles that look representative of the population of all 60 circles. Mark your five circles by clicking on each of them. They will turn orange. Record the average diameter for the five circles. (Make sure you have five orange circles before you record the average diameter.)
- Reset the simulation.
- Choose another five circles and record the average diameter for this sample of circles. You can reuse a circle, but the sample should not have all the same circles. You now have the averages for two samples.
- Reset and repeat for a total of 10 samples. Record the average diameter for each sample.
Click here to open this simulation in its own window.
An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/sss/?p=36
Now we estimate the average diameter of the 60 circles using random samples.
Instructions: Use the simulation below for this activity. You will again see the same 60 circles. As before, this is the “population.” Our goal is to estimate the average diameter of these 25 circles by choosing a random sample.
- Click on the “Generate sample” button to get a random sample of five circles by clicking on the random sample button. The simulation randomly chooses five circles. Record the average diameter for the random sample.
- Reset the simulation using the reset button.
- Click on the “Generate sample” button to get another random sample. Record the average diameter for this random sample. You now have the averages for two samples.
- Reset and repeat for a total of 10 samples. Record the average diameter for each sample.
Click here to open this simulation in its own window.
An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/sss/?p=36
Learn By Doing
Comment
Random selection also guarantees that the sample results do not change haphazardly from sample to sample. When we use random selection, the variability we see in sample results is due to chance. The results obey the mathematical laws of probability. We looked at this idea briefly in the Big Picture of Statistics. Probability is the machinery for drawing conclusions about a population on the basis of samples. To use this machinery, the sample must be chosen by random chance.
Learn By Doing
Learn By Doing
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution

