10.2: How to Write Balanced Chemical Equations
- Last updated
- Save as PDF
- Page ID
- 118829
Learning Objectives
- Explain the roles of subscripts and coefficients in chemical equations.
- Balance a chemical equation when given the unbalanced equation.
- Explain the role of the Law of Conservation of Mass in a chemical reaction.
Even though chemical compounds are broken up and new compounds are formed during a chemical reaction, atoms in the reactants do not disappear, nor do new atoms appear to form the products. In chemical reactions, atoms are never created or destroyed. The same atoms that were present in the reactants are present in the products—they are merely reorganized into different arrangements. In a complete chemical equation, the two sides of the equation must be present on the reactant and the product sides of the equation.
Coefficients and Subscripts
There are two types of numbers that appear in chemical equations. There are subscripts, which are part of the chemical formulas of the reactants and products; and there are coefficients that are placed in front of the formulas to indicate how many molecules of that substance is used or produced.
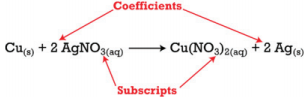
The subscripts are part of the formulas and once the formulas for the reactants and products are determined, the subscripts may not be changed. The coefficients indicate the number of each substance involved in the reaction and may be changed in order to balance the equation. The equation above indicates that one mole of solid copper is reacting with two moles of aqueous silver nitrate to produce one mole of aqueous copper (II) nitrate and two atoms of solid silver.
Balancing a Chemical Equation
Because the identities of the reactants and products are fixed, the equation cannot be balanced by changing the subscripts of the reactants or the products. To do so would change the chemical identity of the species being described, as illustrated in Figure \(\PageIndex{1}\).
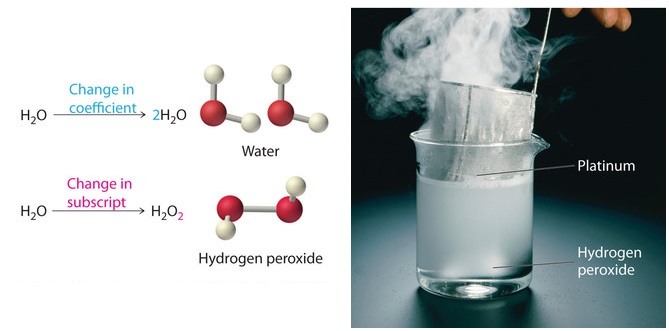
Original molecule \(\ce{H2O}\): if the coefficient 2 is added in front, that makes 2 water molecules; but if the subscript 2 is added to make \(\ce{H2O2}\), that's hydrogen peroxide.
The simplest and most generally useful method for balancing chemical equations is “inspection,” better known as trial and error. The following is an efficient approach to balancing a chemical equation using this method.
Steps in Balancing a Chemical Equation
- Identify the most complex substance.
- Beginning with that substance, choose an element(s) that appears in only one reactant and one product, if possible. Adjust the coefficients to obtain the same number of atoms of this element(s) on both sides.
- Balance polyatomic ions (if present on both sides of the chemical equation) as a unit.
- Balance the remaining atoms, usually ending with the least complex substance and using fractional coefficients if necessary. If a fractional coefficient has been used, multiply both sides of the equation by the denominator to obtain whole numbers for the coefficients.
- Count the numbers of atoms of each kind on both sides of the equation to be sure that the chemical equation is balanced.
Example \(\PageIndex{1}\): Combustion of Heptane
Balance the chemical equation for the combustion of Heptane (\(\ce{C_7H_{16}}\)).
\[\ce{C_7H_{16} (l) + O_2 (g) → CO_2 (g) + H_2O (g) } \nonumber \]
Solution
| Steps | Example |
|---|---|
| 1. Identify the most complex substance. | The most complex substance is the one with the largest number of different atoms, which is \(C_7H_{16}\). We will assume initially that the final balanced chemical equation contains 1 molecule or formula unit of this substance. |
| 2. Adjust the coefficients. |
a. Because one molecule of n-heptane contains 7 carbon atoms, we need 7 \(\ce{CO2}\) molecules, each of which contains 1 carbon atom, on the right side: \[\ce{C7H16 (l) + O2 (g) → } \underline{7} \ce{CO2 (g) + H2O (g) } \nonumber \]
b. Because one molecule of n-heptane contains 16 hydrogen atoms, we need 8 \(\ce{H2O}\) molecules, each of which contains 2 hydrogen atoms, on the right side: \[\ce{C7H16 (l) + O2 (g) → 7 CO2 (g) + } \underline{8} \ce{H2O (g) } \nonumber \]
|
| 3. Balance polyatomic ions as a unit. | There are no polyatomic ions to be considered in this reaction. |
| 4. Balance the remaining atoms. |
The carbon and hydrogen atoms are now balanced, but we have 22 oxygen atoms on the right side and only 2 oxygen atoms on the left. We can balance the oxygen atoms by adjusting the coefficient in front of the least complex substance, O2, on the reactant side: \[\ce{C7H16 (l) + }\underline{11} \ce{ O2 (g) → 7 CO2 (g) + 8H2O (g) } \nonumber \]
|
| 5. Check your work. | The equation is now balanced, and there are no fractional coefficients: there are 7 carbon atoms, 16 hydrogen atoms, and 22 oxygen atoms on each side. Always check to be sure that a chemical equation is balanced. |
Example \(\PageIndex{2}\): Combustion of Isooctane
Combustion of Isooctane (\(\ce{C_8H_{18}}\))
\[\ce{C8H18 (l) + O2 (g) -> CO_2 (g) + H_2O(g)} \nonumber \]
Solution
The assumption that the final balanced chemical equation contains only one molecule or formula unit of the most complex substance is not always valid, but it is a good place to start. The combustion of any hydrocarbon with oxygen produces carbon dioxide and water.
| Steps | Example |
|---|---|
| 1. Identify the most complex substance. | The most complex substance is the one with the largest number of different atoms, which is \(\ce{C8H18}\). We will assume initially that the final balanced chemical equation contains 1 molecule or formula unit of this substance. |
| 2. Adjust the coefficients. |
a. The first element that appears only once in the reactants is carbon: 8 carbon atoms in isooctane means that there must be 8 CO2 molecules in the products: \[\ce{C8H18 (l) + O2 (g) -> }\underline{8} \ce{ CO2 (g) + H2O(g)}\nonumber \]
b. 18 hydrogen atoms in isooctane means that there must be 9 H2O molecules in the products: \[\ce{C8H18 (l) + O2 (g) -> 8CO2 (g) + }\underline{9} \ce{ H2O(g)} \nonumber \]
|
| 3. Balance polyatomic ions as a unit. | There are no polyatomic ions to be considered in this reaction. |
| 4. Balance the remaining atoms. |
The carbon and hydrogen atoms are now balanced, but we have 25 oxygen atoms on the right side and only 2 oxygen atoms on the left. We can balance the least complex substance, O2, but because there are 2 oxygen atoms per O2 molecule, we must use a fractional coefficient (\(\dfrac{25}{2}\)) to balance the oxygen atoms: \[\ce{C8H18 (l) + } \underline{ \dfrac{25}{2} } \ce{O2 (g)→ 8CO2 (g) + 9H2O(g) }\nonumber \]
The equation is now balanced, but we usually write equations with whole number coefficients. We can eliminate the fractional coefficient by multiplying all coefficients on both sides of the chemical equation by 2: \[ \underline{2} \ce{C8H18(l) + } \underline{25} \ce{O2(g) ->} \underline{16} \ce{CO2(g) + } \underline{18} \ce{H2O(g)} \nonumber \] |
| 5. Check your work. |
The balanced chemical equation has 16 carbon atoms, 36 hydrogen atoms, and 50 oxygen atoms on each side. Balancing equations requires some practice on your part as well as some common sense. If you find yourself using very large coefficients or if you have spent several minutes without success, go back and make sure that you have written the formulas of the reactants and products correctly. |
Example \(\PageIndex{3}\): Precipitation of Lead (II) Chloride
Aqueous solutions of lead (II) nitrate and sodium chloride are mixed. The products of the reaction are an aqueous solution of sodium nitrate and a solid precipitate of lead (II) chloride. Write the balanced chemical equation for this reaction.
Solution
| Steps | Example |
|---|---|
| 1. Identify the most complex substance. |
The most complex substance is lead (II) chloride. \[\ce{Pb(NO3)2(aq) + NaCl(aq) → NaNO3(aq) + PbCl2(s)} \nonumber \] |
| 2. Adjust the coefficients. |
There are twice as many chloride ions in the reactants as there are in the products. Place a 2 in front of the NaCl in order to balance the chloride ions. \[\ce{Pb(NO3)2(aq) + }\underline{ 2} \ce{NaCl(aq) → NaNO3(aq) + PbCl2(s)} \nonumber \]
|
| 3. Balance polyatomic ions as a unit. |
The nitrate ions are still unbalanced. Place a 2 in front of the NaNO3. The result is: \[\ce{Pb(NO3)2(aq) + 2NaCl(aq) → } \underline {2} \ce{NaNO3(aq) + PbCl2(s)} \nonumber \]
|
| 4. Balance the remaining atoms. | There is no need to balance the remaining atoms because they are already balanced. |
| 5. Check your work. |
\[\ce{Pb(NO3)2(aq) + 2NaCl(aq) → 2NaNO3(aq) + PbCl2(s)} \nonumber \]
|
Exercise \(\PageIndex{1}\)
Is each chemical equation balanced?
- \(\ce{2Hg(ℓ)+ O_2(g) \rightarrow Hg_2O_2(s)}\)
- \(\ce{C_2H_4(g) + 2O_2(g)→ 2CO_2(g) + 2H_2O(g)}\)
- \(\ce{Mg(NO_3)_2(s) + 2Li (s) \rightarrow Mg(s)+ 2LiNO_3(s)}\)
- Answer a
- yes
- Answer b
- no
- Answer c
- yes
Exercise \(\PageIndex{2}\)
Balance the following chemical equations.
- \(\ce{N2 (g) + O2 (g) → NO2 (g) }\)
- \(\ce{Pb(NO3)2(aq) + FeCl3(aq) → Fe(NO3)3(aq) + PbCl2(s)}\)
- \(\ce{C6H14(l) + O2(g)→ CO2(g) + H2O(g)}\)
- Answer a
- N2 (g) + 2O2 (g) → 2NO2 (g)
- Answer b
- 3Pb(NO3)2(aq) + 2FeCl3(aq) → 2Fe(NO3)3(aq) + 3PbCl2(s)
- Answer c
- 2C6H14(l) + 19O2(g)→ 12CO2(g) + 14H2O(g)
Summary
- To be useful, chemical equations must always be balanced. Balanced chemical equations have the same number and type of each atom on both sides of the equation.
- The coefficients in a balanced equation must be the simplest whole number ratio. Mass is always conserved in chemical reactions.
Vocabulary
- Chemical reaction - The process in which one or more substances are changed into one or more new substances.
- Reactants - The starting materials in a reaction.
- Products - Materials present at the end of a reaction.
- Balanced chemical equation - A chemical equation in which the number of each type of atom is equal on the two sides of the equation.
- Subscripts - Part of the chemical formulas of the reactants and products that indicate the number of atoms of the preceding element.
- Coefficient - A small whole number that appears in front of a formula in a balanced chemical equation.

