17.7: Electrolysis
- Last updated
- Save as PDF
- Page ID
- 112984
Learning Objectives
- Describe electrolytic cells and their relationship to galvanic cells
- Perform various calculations related to electrolysis
In galvanic cells, chemical energy is converted into electrical energy. The opposite is true for electrolytic cells. In electrolytic cells, electrical energy causes nonspontaneous reactions to occur in a process known as electrolysis. The charging electric barttery shows one such process. Electrical energy is converted into the chemical energy in the battery as it is charged. Once charged, the battery can be used to power the automobile. The same principles are involved in electrolytic cells as in galvanic cells. We will look at three electrolytic cells and the quantitative aspects of electrolysis.
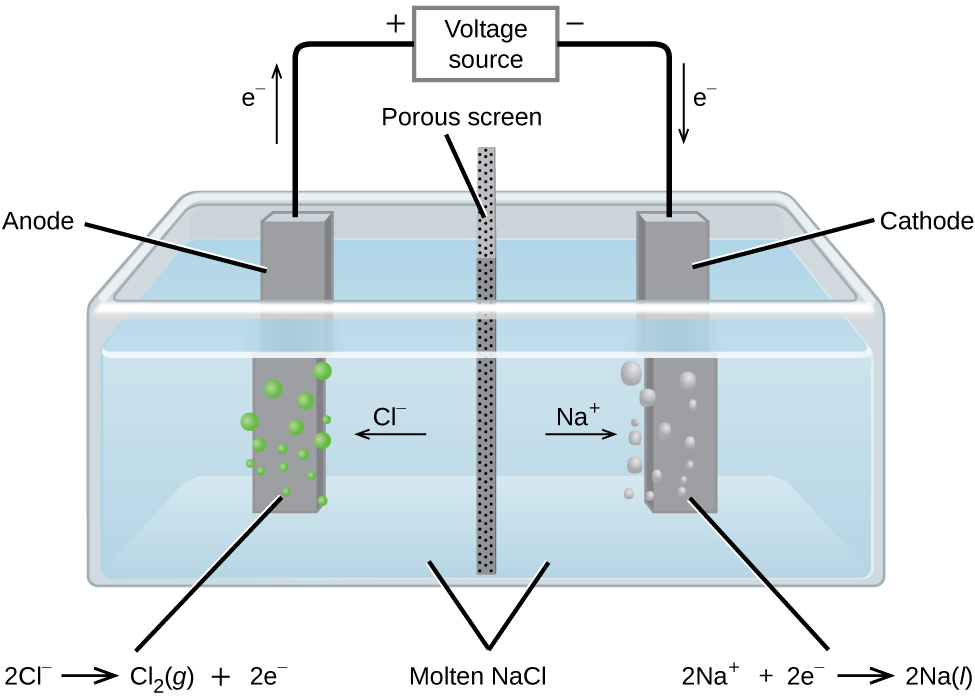
The Electrolysis of Molten Sodium Chloride
In molten sodium chloride, the ions are free to migrate to the electrodes of an electrolytic cell. A simplified diagram of the cell commercially used to produce sodium metal and chlorine gas is shown in Figure \(\PageIndex{1}\). Sodium is a strong reducing agent and chlorine is used to purify water, and is used in antiseptics and in paper production. The reactions are
\[\begin{align}
&\textrm{anode: }\ce{2Cl-}(l) ⟶\ce{Cl2}(g)+\ce{2e-} \hspace{20px}E^\circ_{\ce{Cl2/Cl-}}=\mathrm{+1.3\: V}\\
&\textrm{cathode: }\ce{Na+}(l)+\ce{e-} ⟶\ce{Na}(l) \hspace{20px}E^\circ_{\ce{Na+/Na}}=\mathrm{−2.7\: V}\\
& \overline{\textrm{overall: } \ce{2Na+}(l)+\ce{2Cl-}(l) ⟶\ce{2Na}(l)+\ce{Cl2}(g) \hspace{20px}E^\circ_\ce{cell}=\mathrm{−4.0\: V}}
\end{align} \nonumber \]
The power supply (battery) must supply a minimum of 4 V, but, in practice, the applied voltages are typically higher because of inefficiencies in the process itself.
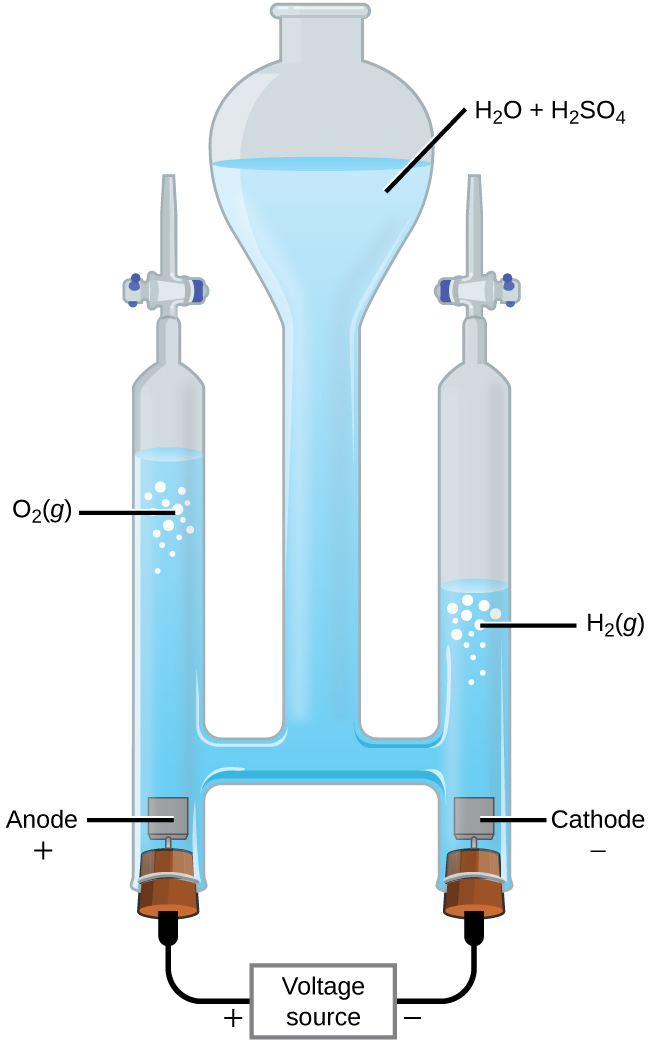
The Electrolysis of Water
It is possible to split water into hydrogen and oxygen gas by electrolysis. Acids are typically added to increase the concentration of hydrogen ion in solution (Figure \(\PageIndex{2}\)). The reactions are
\[\begin{align}
&\textrm{anode: }\ce{2H2O}(l)⟶\ce{O2}(g)+\ce{4H+}(aq)+\ce{4e-} \hspace{20px} E^\circ_\ce{anode}=\mathrm{+1.229\: V}\\
&\textrm{cathode: }\ce{2H+}(aq)+\ce{2e-}⟶\ce{H2}(g) \hspace{20px} E^\circ_\ce{cathode}=\mathrm{0\: V}\\
&\overline{\textrm{overall: }\ce{2H2O}(l)⟶\ce{2H2}(g)+\ce{O2}(g) \hspace{20px} E^\circ_\ce{cell}=\mathrm{−1.229\: V}}
\end{align} \nonumber \]
Note that the sulfuric acid is not consumed and that the volume of hydrogen gas produced is twice the volume of oxygen gas produced. The minimum applied voltage is 1.229 V.
The Electrolysis of Aqueous Sodium Chloride
The electrolysis of aqueous sodium chloride is the more common example of electrolysis because more than one species can be oxidized and reduced. Considering the anode first, the possible reactions are
\[\begin{align}
&\textrm{(i) }\ce{2Cl-}(aq)⟶\ce{Cl2}(g)+\ce{2e-} \hspace{20px} E^\circ_\ce{anode}=\mathrm{+1.35827\: V}\\
&\textrm{(ii) }\ce{2H2O}(l)⟶\ce{O2}(g)+\ce{4H+}(aq)+\ce{4e-} \hspace{20px} E^\circ_\ce{anode}=\mathrm{+1.229\: V}
\end{align} \nonumber \]
These values suggest that water should be oxidized at the anode because a smaller potential would be needed—using reaction (ii) for the oxidation would give a less-negative cell potential. When the experiment is run, it turns out chlorine, not oxygen, is produced at the anode. The unexpected process is so common in electrochemistry that it has been given the name overpotential. The overpotential is the difference between the theoretical cell voltage and the actual voltage that is necessary to cause electrolysis. It turns out that the overpotential for oxygen is rather high and effectively makes the reduction potential more positive. As a result, under normal conditions, chlorine gas is what actually forms at the anode.
Now consider the cathode. Three reductions could occur:
\[\begin{align}
&\textrm{(iii) }\ce{2H+}(aq)+\ce{2e-}⟶\ce{H2}(g) \hspace{20px} E^\circ_\ce{cathode}=\mathrm{0\: V}\\
&\textrm{(iv) }\ce{2H2O}(l)+\ce{2e-}⟶\ce{H2}(g)+\ce{2OH-}(aq) \hspace{20px} E^\circ_\ce{cathode}=\mathrm{−0.8277\:V}\\
&\textrm{(v) }\ce{Na+}(aq)+\ce{e-}⟶\ce{Na}(s) \hspace{20px} E^\circ_\ce{cathode}=\mathrm{−2.71\: V}
\end{align} \nonumber \]
Reaction (v) is ruled out because it has such a negative reduction potential. Under standard state conditions, reaction (iii) would be preferred to reaction (iv). However, the pH of a sodium chloride solution is 7, so the concentration of hydrogen ions is only 1× 10−7 M. At such low concentrations, reaction (iii) is unlikely and reaction (iv) occurs. The overall reaction is then
\[\textrm{overall: }\ce{2H2O}(l)+\ce{2Cl-}(aq)⟶\ce{H2}(g)+\ce{Cl2}(g)+\ce{2OH-}(aq) \hspace{20px} E^\circ_\ce{cell}=\mathrm{−2.186\: V} \nonumber \]
As the reaction proceeds, hydroxide ions replace chloride ions in solution. Thus, sodium hydroxide can be obtained by evaporating the water after the electrolysis is complete. Sodium hydroxide is valuable in its own right and is used for things like oven cleaner, drain opener, and in the production of paper, fabrics, and soap.
Electroplating
An important use for electrolytic cells is in electroplating. Electroplating results in a thin coating of one metal on top of a conducting surface. Reasons for electroplating include making the object more corrosion resistant, strengthening the surface, producing a more attractive finish, or for purifying metal. The metals commonly used in electroplating include cadmium, chromium, copper, gold, nickel, silver, and tin. Common consumer products include silver-plated or gold-plated tableware, chrome-plated automobile parts, and jewelry. We can get an idea of how this works by investigating how silver-plated tableware is produced (Figure \(\PageIndex{3}\)).
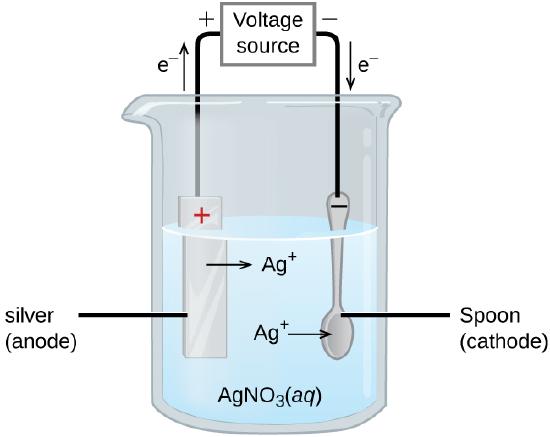
In the figure, the anode consists of a silver electrode, shown on the left. The cathode is located on the right and is the spoon, which is made from inexpensive metal. Both electrodes are immersed in a solution of silver nitrate. As the potential is increased, current flows. Silver metal is lost at the anode as it goes into solution.
\[\textrm{anode: }\ce{Ag}(s)⟶\ce{Ag+}(aq)+\ce{e-} \nonumber \]
The mass of the cathode increases as silver ions from the solution are deposited onto the spoon
\[\textrm{cathode: }\ce{Ag+}(aq)+\ce{e-}⟶\ce{Ag}(s) \nonumber \]
The net result is the transfer of silver metal from the anode to the cathode. The quality of the object is usually determined by the thickness of the deposited silver and the rate of deposition.
Quantitative Aspects of Electrolysis
The amount of current that is allowed to flow in an electrolytic cell is related to the number of moles of electrons. The number of moles of electrons can be related to the reactants and products using stoichiometry. Recall that the SI unit for current (I) is the ampere (A), which is the equivalent of 1 coulomb per second (1 A = \(\mathrm{1\: \dfrac{C}{s}}\)). The total charge (Q, in coulombs) is given by
\[Q=I×t=n×F \nonumber \]
where
- t is the time in seconds,
- n the number of moles of electrons, and
- F is the Faraday constant.
Moles of electrons can be used in stoichiometry problems. The time required to deposit a specified amount of metal might also be requested, as in the second of the following examples.
Example \(\PageIndex{1}\): Converting Current to Moles of Electrons
In one process used for electroplating silver, a current of 10.23 A was passed through an electrolytic cell for exactly 1 hour. How many moles of electrons passed through the cell? What mass of silver was deposited at the cathode from the silver nitrate solution?
Solution
Faraday’s constant can be used to convert the charge (Q) into moles of electrons (n). The charge is the current (I) multiplied by the time
\[n=\dfrac{Q}{F}=\mathrm{\dfrac{\dfrac{10.23\: C}{s}×1\: hr×\dfrac{60\: min}{hr}×\dfrac{60\:s}{min}}{96,485\: C/mol\: e^-}=\dfrac{36,830\: C}{96,485\: C/mol\:e^-}=0.3817\: mol\: e^-} \nonumber \]
From the problem, the solution contains AgNO3, so the reaction at the cathode involves 1 mole of electrons for each mole of silver
\[\textrm{cathode: }\ce{Ag+}(aq)+\ce{e-}⟶\ce{Ag}(s) \nonumber \]
The atomic mass of silver is 107.9 g/mol, so
\[\mathrm{mass\: Ag=0.3817\: mol\: e^-×\dfrac{1\: mol\: Ag}{1\: mol\: e^-}×\dfrac{107.9\: g\: Ag}{1\: mol\: Ag}=41.19\: g\: Ag} \nonumber \]
Check your answer: From the stoichiometry, 1 mole of electrons would produce 1 mole of silver. Less than one-half a mole of electrons was involved and less than one-half a mole of silver was produced.
Exercise \(\PageIndex{1}\)
Aluminum metal can be made from aluminum ions by electrolysis. What is the half-reaction at the cathode? What mass of aluminum metal would be recovered if a current of 2.50 × 103 A passed through the solution for 15.0 minutes? Assume the yield is 100%.
- Answer
-
\(\ce{Al^3+}(aq)+\ce{3e-}⟶\ce{Al}(s)\); 7.77 mol Al = 210.0 g Al.
Example \(\PageIndex{2}\): Time Required for Deposition
In one application, a 0.010-mm layer of chromium must be deposited on a part with a total surface area of 3.3 m2 from a solution of containing chromium(III) ions. How long would it take to deposit the layer of chromium if the current was 33.46 A? The density of chromium (metal) is 7.19 g/cm3.
Solution This problem brings in a number of topics covered earlier. An outline of what needs to be done is:
- If the total charge can be determined, the time required is just the charge divided by the current
- The total charge can be obtained from the amount of Cr needed and the stoichiometry
- The amount of Cr can be obtained using the density and the volume Cr required
- The volume Cr required is the thickness times the area
Solving in steps, and taking care with the units, the volume of Cr required is
\[\mathrm{volume=\left(0.010\: mm×\dfrac{1\: cm}{10\: mm}\right)×\left(3.3\:m^2×\left(\dfrac{10,000\:cm^2}{1\:m^2}\right)\right)=33\: cm^3} \nonumber \]
Cubic centimeters were used because they match the volume unit used for the density. The amount of Cr is then
\[\mathrm{mass=volume×density=33\cancel{cm^3}×\dfrac{7.19\: g}{\cancel{cm^3}}=237\: g\: Cr} \nonumber \]
\[\mathrm{mol\: Cr=237\: g\: Cr×\dfrac{1\: mol\: Cr}{52.00\: g\: Cr}=4.56\: mol\: Cr} \nonumber \]
Since the solution contains chromium(III) ions, 3 moles of electrons are required per mole of Cr. The total charge is then
\[Q=\mathrm{4.56\: mol\: Cr×\dfrac{3\:mol\: e^-}{1\: mol\: Cr}×\dfrac{96485\: C}{mol\: e^-}=1.32×10^6\:C} \nonumber \]
The time required is then
\[t=\dfrac{Q}{I}=\mathrm{\dfrac{1.32×10^6\:C}{33.46\: C/s}=3.95×10^4\:s=11.0\: hr} \nonumber \]
Check your answer: In a long problem like this, a single check is probably not enough. Each of the steps gives a reasonable number, so things are probably correct. Pay careful attention to unit conversions and the stoichiometry.
Exercise \(\PageIndex{2}\)
What mass of zinc is required to galvanize the top of a 3.00 m × 5.50 m sheet of iron to a thickness of 0.100 mm of zinc? If the zinc comes from a solution of Zn(NO3)2 and the current is 25.5 A, how long will it take to galvanize the top of the iron? The density of zinc is 7.140 g/cm3.
- Answer
-
231 g Zn required 23,000 minutes.
Summary
Using electricity to force a nonspontaneous process to occur is electrolysis. Electrolytic cells are electrochemical cells with negative cell potentials (meaning a positive Gibbs free energy), and so are nonspontaneous. Electrolysis can occur in electrolytic cells by introducing a power supply, which supplies the energy to force the electrons to flow in the nonspontaneous direction. Electrolysis is done in solutions, which contain enough ions so current can flow. If the solution contains only one material, like the electrolysis of molten sodium chloride, it is a simple matter to determine what is oxidized and what is reduced. In more complicated systems, like the electrolysis of aqueous sodium chloride, more than one species can be oxidized or reduced and the standard reduction potentials are used to determine the most likely oxidation (the half-reaction with the largest [most positive] standard reduction potential) and reduction (the half-reaction with the smallest [least positive] standard reduction potential). Sometimes unexpected half-reactions occur because of overpotential. Overpotential is the difference between the theoretical half-reaction reduction potential and the actual voltage required. When present, the applied potential must be increased, making it possible for a different reaction to occur in the electrolytic cell. The total charge, Q, that passes through an electrolytic cell can be expressed as the current (I) multiplied by time (Q = It) or as the moles of electrons (n) multiplied by Faraday’s constant (Q = nF). These relationships can be used to determine things like the amount of material used or generated during electrolysis, how long the reaction must proceed, or what value of the current is required.
Summary
- electrolysis
- process using electrical energy to cause a nonspontaneous process to occur
- electrolytic cell
- electrochemical cell in which electrolysis is used; electrochemical cell with negative cell potentials
- electroplating
- depositing a thin layer of one metal on top of a conducting surface
- overpotential
- difference between the theoretical potential and actual potential in an electrolytic cell; the “extra” voltage required to make some nonspontaneous electrochemical reaction to occur


