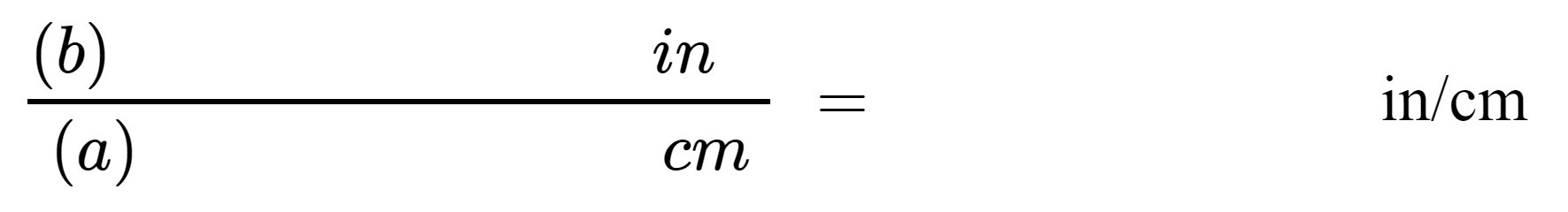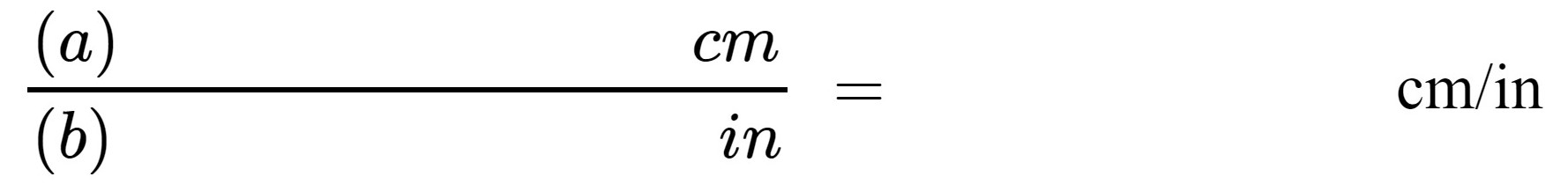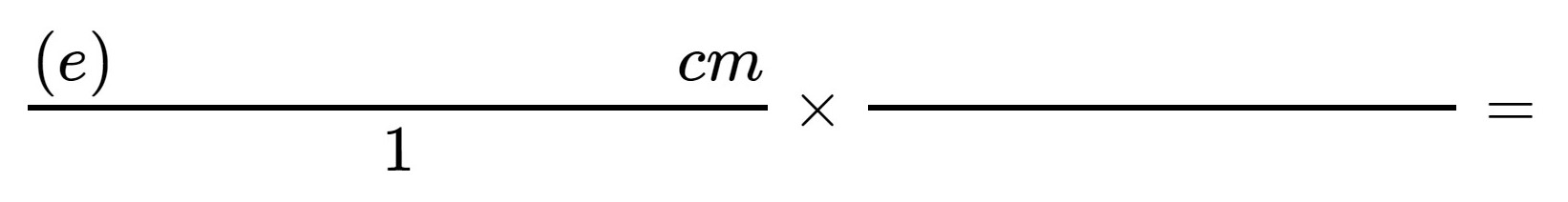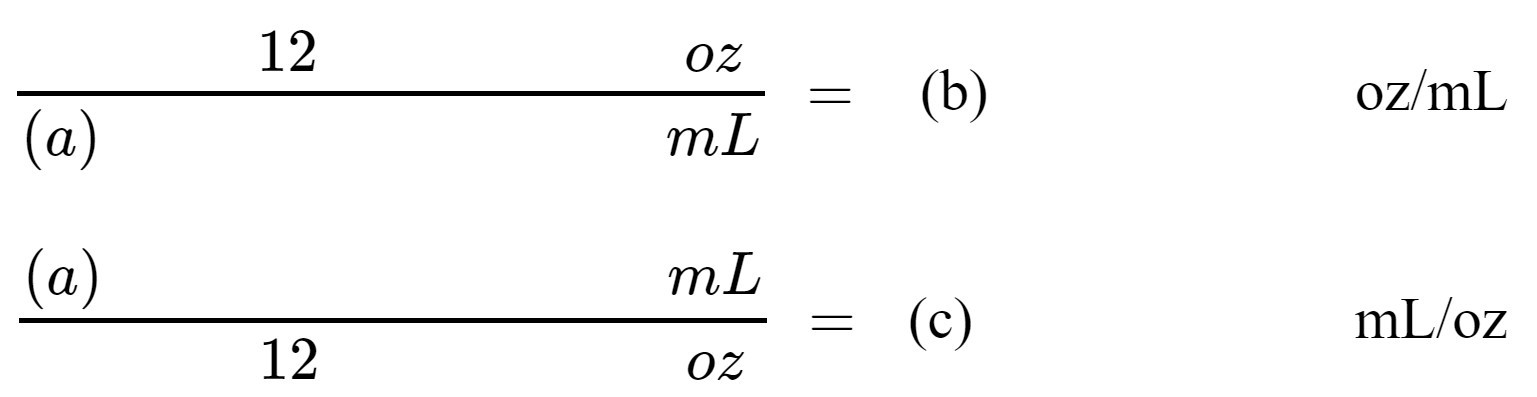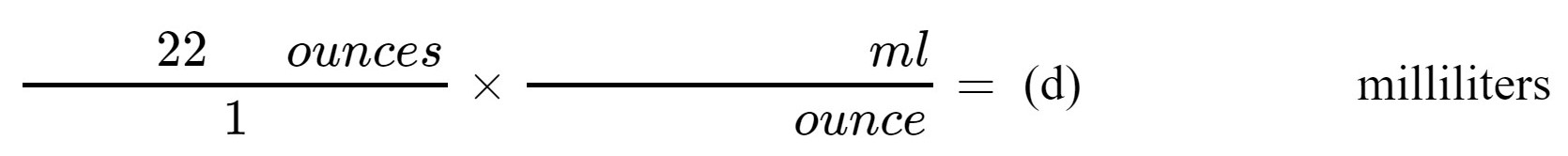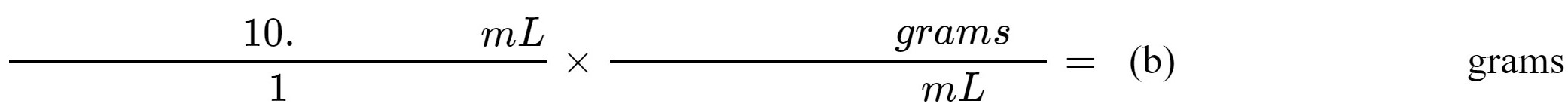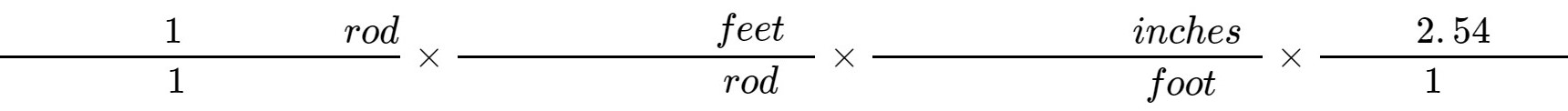Experiment_601_Measurement 1_6

Last updated
Save as PDF

Page ID: 302983

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Student Name

Laboratory Date:

Date Report Submitted:

___________________________

Student ID

Experiment Number and Title

Experiment 601: Measurement & Dimensional Analysis

Experiment 601: Measurement & Dimensional Analysis

Section 1: Purpose and Summary

Describe how the English and metric systems of measurement compare.
Learn how to convert between different units of measurement.

In this experiment, students will practice measuring the following parameters: length, mass, volume, and temperature. Students will calculate derived constants including density and heat capacity. Students will practice converting from units in the English system to the metric system. Students will learn dimensional analysis, common prefixes and selected conversion factors.

Note: When a parameter is determined, it needs to have both a number and the unit of measurement to be complete. If you only write down the number “5”, for example, is it “5 inches”, “5 centimeters”, “5 meters” or “5 miles”?

Note: When writing decimals between zero and 1, a good practice is to include the leading ‘0’ before the decimal point. For example, if you write “.125” centimeters onto your data report, it is possible that you might accidentally misinterpret the value as 125 centimeters. But if you write “0.125” centimeters there should be no question that there is a decimal point present.

Section 2: Safety Precautions and Waste Disposal

Safety Precautions:

All of the materials in this experiment are harmless. Use of eye protection is recommended for all experimental procedures.

Waste Disposal:

No waste will be generated for this experiment.

Section 3: Procedure

Part 1: LENGTH

1. Using a large ruler, carefully measure the width of your lab bench in centimeters and in inches. Remember to use proper significant figures.

Width of bench:

(a) _________________cm

(b) _________________in

2. These two measurements allow us to create a pair of conversion factors between centimeters and inches. A conversion factor (also called a unit factor) is a ratio which can be multiplied by a measurement expressed in one set of units, to convert the measurement to a new set of units.

To find a conversion factor for converting centimeters to inches, divide measurement (b) by measurement (a):

Report your calculated conversion factor between inches and centimeters here:

(c)________________in/cm

3. To find a conversion factor for converting inches to centimeters, divide measurement (a) by measurement (b):

Report your calculated conversion factor between centimeters and inches here:

(d)________________cm/in

4. Obtain a numbered card with a line of unknown length.

Measure the line to the tenth of a centimeter (0.1 cm), and convert this measurement to inches using the appropriate conversion factor from your work in Step 2, above.

Show your work here:

Hint: Any quantity can be written as a fraction over 1. If the units cancel, you have selected the proper conversion factor.

Card # ________________

Length:

(e) _______________ cm

Calculate the length in inches:

(f) Length: ______________in

5. Measure the height of your lab partner in inches. Convert this measurement to centimeters using the appropriate conversion factor from Step 3. Remember to include the units on each quantity.

Show your work here:

Height in inches

(g) _______________ in

Calculate the height in centimeters:

(h) Height: _____________cm

Part 2: MASS

1. Obtain one of the numbered metal slugs. Measure and record its mass to the hundredth of a gram (0.01 g). Keep this metal slug for volume measurement in Part 3 of this experiment.

Slug # ________________

(a) _______________ grams

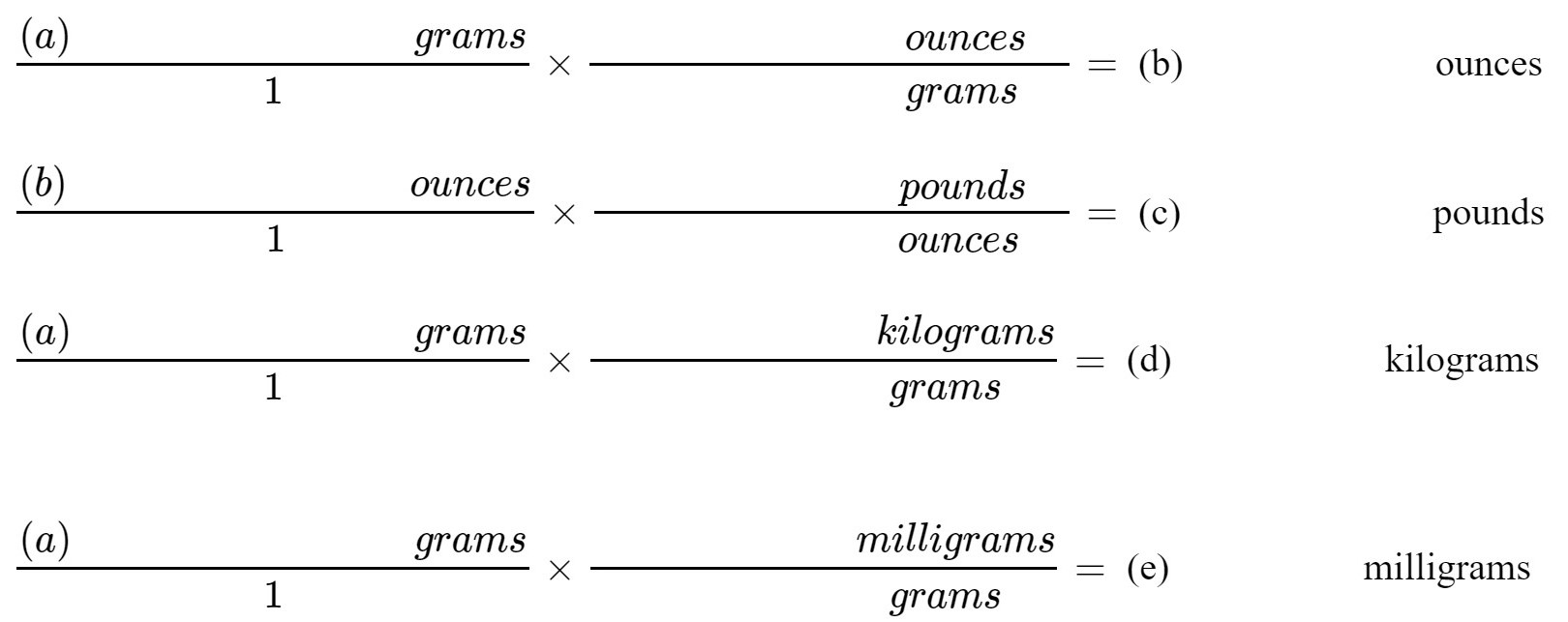
2. Using the appropriate conversion factors from Tables I and II (page 8), convert the mass of the slug into ounces, pounds, kilograms and milligrams:

Show your work here:

(b) ________________ ounces

(c)________________ pounds

(d)______________ kilograms

(e) milligrams

Part 3: VOLUME

1. Fill a measuring cup with tap water, so that the bottom of the meniscus rests exactly on the 12-ounce mark. Give your best estimate of how many milliliters (mL) this represents.

NOTE: Because the symbol for liters is both “l”, and “L”, the symbol for milliliters can be either “ml” or “mL”. When taking notes, use whichever symbol provides the clearer meaning and be consistent.

(a) _________________ mL

2. Use your measurements to calculate a conversion factor from ounces to milliliters and milliliters to ounces.

Show your work here:

Report your calculated conversion factor here:

(b) ________________oz/mL

(c)________________ mL/oz

3. A large bottle of beer contains 22 ounces of fluid. Using the appropriate conversion factor from Step 2 above, convert the volume of this beer into milliliters.

Show your work here:

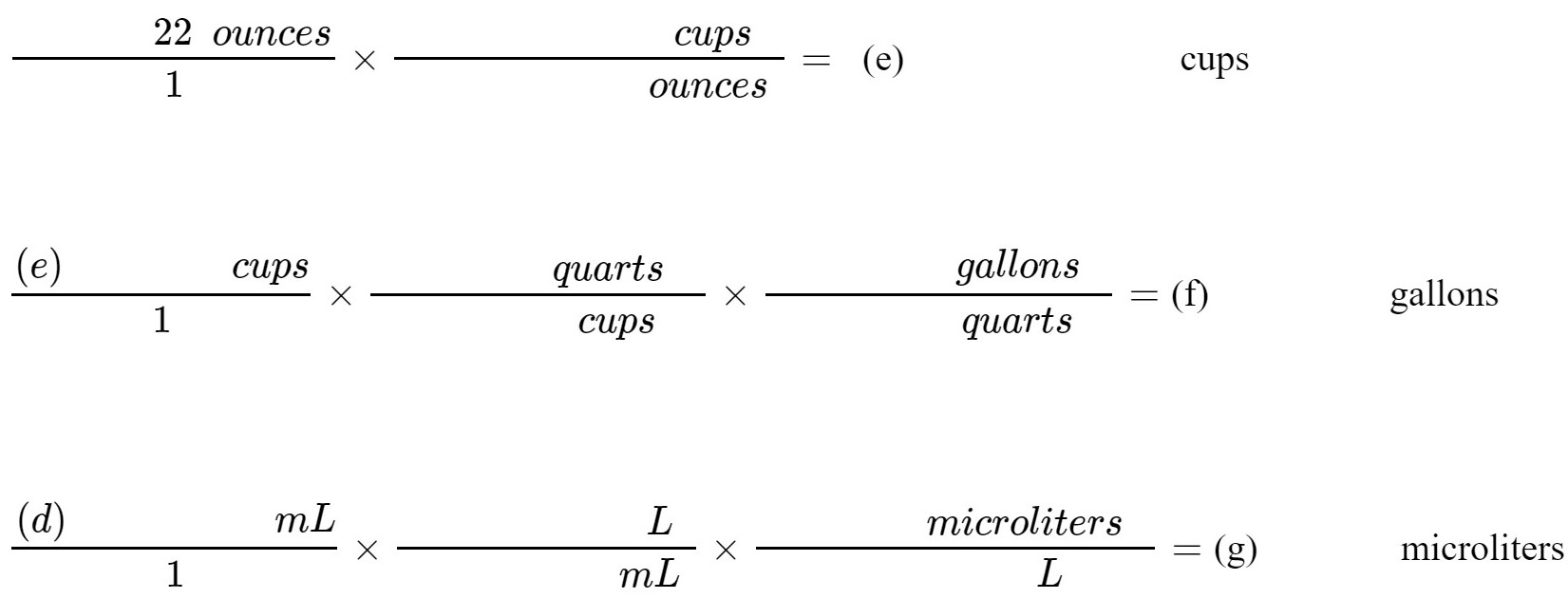
Using the appropriate conversion factor from Table II (page 8), convert the volume of this beer into cups, gallons, and microliters.

Show your work here:

NOTE: The symbol for micro is the Greek letter mu, “μ”

(d) milliliters

(e) cups

(f) gallons

(g) μL

4. Take your metal slug from Part 2 of this experiment. Fill a 50-mL graduated cylinder with tap water to about the 35-mL mark. Record the exact volume of water.

Volume of water:

(h) mL

5. Tilt the graduated cylinder and carefully slide the metal slug into the cylinder. Record the final volume of water.

Volume of water after addition of metal slug:

6. The volume of the metal slug is equivalent to the amount by which the water level rises when the metal is submerged. Calculate the volume of the metal slug: (i) – (h)

Volume of metal slug:

(j) mL

Part 4: DENSITY

The mass of a substance divided by its volume is called its density, thus

Density= $\frac{\text { mass } \quad \text { } }{volume} $

Using the mass and the volume of the metal slug you measured in Parts 2 and 3, calculate its density in units of g/mL?

Show your work here:

(a) _________________ g/mL

2. The density of the metal slug that you calculated in Step 1 above can be used as a conversion factor.

What would be the mass in grams of 10. mL of this substance?

(b)________________ grams

3. What volume, in milliliters (mL), would be occupied by 375 grams of this metal?

Show your work here:

NOTE: Density is *not* a quantity, but a property of a material. A mass of an item depends on the quantity of matter in it. The density is how compact that matter is within the space it occupies. The units on both are different.

Part 5: TEMPERATURE & SPECIFIC HEAT

1. Remove your Celsius (centigrade) thermometer from its protective case and let it sit for two minutes at room temperature. Record the temperature of the room.

Add 300 milliliters of tap water to your 600 mL beaker. Using the apparatus demonstrated by your instructor, bring this water to a rolling boil.

Measure the temperature of the boiling water and record this value.

Room temperature:

(a) _________________°C

Boiling water temperature:

(b) _________________°C

2. Temperatures in the units of Celsius can be converted to units of Fahrenheit by the formula:

( $\frac{9}{ 5} \quad $ × ℃) +32= ℉

Likewise, Fahrenheit temperatures can be converted to Celsius as follows:

$\frac{5}{ 9} \quad $ ×( ℉ − 32)= ℃

Using the appropriate formula, find the temperature of the room in degrees Fahrenheit.

Show your work here:

Room temperature:

3. The amount of energy needed to raise the temperature of one gram of substance by one degree is called its specific heat. For example, the specific heat of water can be expressed as

1.00 calorie /g°C (or 4.18 Joules/g°C) whereas the specific heat of glass is 0.20 calorie/g°C (or 0.84 Joules/g°C).

Whenever a substance is heated from a lower to higher temperature, or vice versa, the amount of energy absorbed from the surroundings (to heat it) or released to the surroundings (as it cools) can be calculated by this general formula:

energy exchanged = (mass of substance)(specific heat)(temperature change)

The temperature change, usually called delta-T or “ΔT” is simply the final temperature minus the initial temperature:

FIX

ΔT = T _final - T _initial

where T final is the final temperature, and T initial is the initial temperature. Note that ΔT can be either positive or negative.

When water is being considered, and we use units of calories, the equation becomes:

calories exchanged = mass × $\frac{1.00 cal}{ g ℃} \quad $ ×(ΔT)

Let us calculate the number of heat calories absorbed by the water from the Bunsen burner when you boiled it in Step 1 above. We will assume that the water started out at room temperature (even though that might not really be the case).

(d) ΔT = °C - °C = °C

(e) If the density of water is 1.00 g/mL, what is the mass of 300. mL of water?

Show your work here:

(f) Using your calculated values from parts (d) and (e), determine the number of calories absorbed by your heated water:

grams of water x $\frac{1.00 cal}{ g ℃} \quad $ ×(ΔT) x ____ °C = cal

Note: There are 3 units required for specific heat: one unit in the numerator (calorie or Joules) and 2 units in the denominator (grams and Celsius).

(d) ΔT = ^oC

(e) grams

(f) calories

TABLE I: COMMON PREFIXES USED IN THE METRIC SYSTEM
	Giga, G	=	1,000,000,000	=	10⁹
	Mega, M	=	1,000,000	=	10⁶
	kilo, k	=	1,000	=	10³
	deci, d	=	0.1	=	10^-1	=	1/10
	centi, c	=	0.01	=	10^-2	=	1/100
	milli, m	=	0.001	=	10^-3	=	1/1,000
	micro, μ	=	0.000001	=	10^-6	=	1/1,000,000
	nano, n	=	0.000000001	=	10^-9	=	1/1,000,000,000

TABLE II: SELECTED CONVERSION FACTORS
Length
	12 inches (in) = 1 foot (ft)	3 feet = 1 yard (yd)		5,280 feet = 1 mile (mi)
Mass
	16 ounces (oz) = 1 pound (lb)		28 grams (g) = 1 ounce (oz)
Volume
	8 ounces* = 1 cup	16 ounces* = 1 pint		4 cups = 1 quart
	4 quarts = 1 gallon
* The English/American system of measurements uses ounces for both mass and volume. When ounces are used for volume measurements, they are usually written as “fluid ounces”, or “fl. oz.” There is no easy comparison or conversion between ounces used for mass and fluid ounces used for volumes.

Post Lab Questions:

1. An older unit of length used in the English system is the rod. A rod is equal to 16.5 feet. Calculate the number of centimeters that are in 1 rod. Some of the setup for your calculation is below:

=____________

2. In medicine, the grain was used as an older unit of measurement. One grain is equal to 64.79891 milligrams (mg). Often, a 5-grain dosage of aspirin would be prescribed.

Calculate the milligram dosage of a 5-grain tablet of aspirin.

What is a common dosage of aspirin in a tablet for adults? (Search the internet for an answer.) How does it compare with the traditional amount delivered as 5 grains?

3. The karat is a fractional measure of purity for gold. Pure gold is defined to be 24 karats. So 24 karat gold would be (24/24), or 100% gold. 18 karat gold would be 18/24 or 75% gold, with the remainder a different metal in the alloy. The different metal is generally much cheaper than the gold and the cost of that metal can be ignored.

You are on travel in a foreign country. The local unit of currency is the solar. The current exchange rate is 3.26 solars are equivalent to $1.00 (U. S. dollar).

You see a very attractive piece of jewelry that is 14 karat gold. It weighs 25 grams. The spot price of gold today is $38.06 per gram.

The vendor is asking 1200.00 solars for the jewelry. Is this a good deal (based on the value of the gold content)? Show your work.

Notes: