1.3: Handling Large and Small Numbers
- Page ID
- 154957
Example 3 from Measurements, Quantities and Unity Factors illustrates a common occurrence in science—results often involve very large numbers or very small fractions. The United States used 66 500 000 000 000 000 000 J (joules) of energy in 1971, and the mass of a water molecule is 0.000 000 000 000 000 000 000 029 9 g. Such numbers are inconvenient to write and hard to read correctly. (We have divided the digits into groups of three to make it easier to locate the decimal point. Spaces are used instead of commas because many countries use a comma to indicate the decimal.)
There are two ways of handling this problem. We can express a quantity in larger or smaller units, as in Example 4 from Measurements, Quantities and Unity Factors, or we can use a better way to write small and large numbers. The latter approach involves what is called scientific notation or exponential notation. The position of the decimal point is indicated by a power (or exponent) of 10. For example,
\[138= 13.8\cdot 10= 1.38\cdot 10\cdot 10= 1.38\cdot 10^2\]
\[0.004\ 83= \frac{4.83}{10\cdot10\cdot10} = 4.83\cdot\frac{1}{10^3} = 4.83\cdot10^{-3}\]
A number with a negative exponent is simply the reciprocal of (one divided by) the same number with the equivalent positive exponent. Therefore decimal fractions (numbers between zero and one) may be expressed using negative powers of 10. Numbers between 1 and 10 require no exponential part, and those larger than 10 involve positive exponents. By convention the power of 10 is chosen so that there is one digit to the left of the decimal point in the ordinary number. That is, we would usually write 5280 as 5.28 × 103 not as 0.528 × 104 or 52.8 × 102.
To convert a number from ordinary to scientific notation, count how many places the decimal point must be shifted to arrive at a number between 1 and 10. If these shifts are to the left, the number was large to begin with and we multiply by a large (that is, positive) power of 10. If the shift is to the right, a reciprocal (negative) power of 10 must be used.
Example \(\PageIndex{1}\) : Scientific Notation
Express the following numbers in scientific notation: (a) 7563; (b) 0.0156.
Solution:
a) In this case the decimal point must be shifted left three places:

Therefore we use an exponent of +3:
\[7563= 7.563\cdot10^3\]
b) Shifting the decimal point two places to the right yields a number between 1 and 10:

Therefore the exponent is –2:
\[0.0156= 1.56\cdot10^{-2}\]
When working with exponential notation, it is often necessary to add, subtract, multiply, or divide numbers. When multiplying and dividing, you must remember that multiplication corresponds to addition of exponents, and division to their subtraction.
Multiplication: \(\text{10}^a\cdot\text{10}^b = \text{10}^{\small(a + b\small)}\)
Division: \(\frac{10^a}{10^b} = 10^{(a - b)}\)
Hence \((3.0\cdot10^5)\cdot(5.0\cdot10^3) = 15.0\cdot10^{(5+3)}= 15.0\cdot10^8= 1.50\cdot10^9\) and \(\frac{3.0\cdot10^5}{5.0\cdot10^3} =0.6\cdot10^{(5- 3)} = 0.6\cdot10^2= 6.0\cdot10\)
Example \(\PageIndex{2}\) : Exponential Notation
Evaluate the following, giving your answer in correct exponential notation:
- \((3.89 \cdot 10^5) \cdot (1.09 \cdot 10^{-3}) \)
- \((6.41\cdot10^{-5}) \cdot(2.72 \cdot10^{-2})\)
- \(\frac{(5.0\cdot10^6)}{(3.98\cdot10^8)} \)
- \(\frac{(7.53\cdot10^{-3})}{(8.57\cdot10^{-5})} \)
Solution:
- \((3.89\cdot10^5)\cdot(1.09 \cdot10^{-3}) = 3.89\cdot1.09\cdot10^{5 + (-3)}= 4.24\cdot10^2 \)
- \((6.41\cdot10^{-5})\cdot(2.72 \cdot10^{-2})\)= \(6.41\cdot2.72\cdot10^{-5 + (-2)}\) = \(17.43 \cdot10^{-7}\) = \(1.743 \cdot10^{-6}\)
- \(\frac{(5.0\cdot10^6)}{(3.98\cdot10^8)}= \frac{5.0}{3.98} \cdot10^{6-8}= 1.26\cdot10^{-2} \)
- \(\frac{(7.53\cdot10^{-3})}{(8.57\cdot10^{-5})} = \frac{7.53}{8.57}\cdot10^{-3 - (-5)} = 0.879\cdot10^2 = 8.79\cdot10^1 \)
Addition and subtraction require that all numbers be converted to the same power of 10. (This corresponds to lining up the decimal points.)
Example \(\PageIndex{3}\) : Scientific Notation
Evaluate the following, giving your answer in scientific notation:
a)\((6.32\cdot10^2) – (1.83 \cdot10^\cdot{-1}) \)
b)\((3.72 \cdot10^4) + (1.63\cdot10^5) – (1.7 10^3) \)
Solution:
a) First convert to the same power of 10; then add the ordinary numbers.
\( \begin{align}&&6.32\cdot10^2&=& 632 \\&&–1.83\cdot10^{-1}&=& – 0.183 \\632 – 0.183&=& 631.817&=& 6.318 17\cdot10^2 \end{align}\)
b) Convert all powers of 10 to 104.
\( \begin{align}3.72\cdot10^4 &=& 3.72 \cdot10^4 &=& 3.72 × 10^4 \\1.63\cdot10^5&=& 1.63\cdot10 \cdot10^4&=& 16.3 \cdot10^4 \\–1.7 \cdot10^3&=& –1.7 \cdot10^{-1}\cdot10^4&=& – 0.17\cdot10^4 \\ (3.72\cdot10^4) + (16.3\cdot10^4) - (0.17 \cdot10^4)&=& 19.85 \cdot10^4&=& 1.985\cdot10^5\end{align} \)
Scientific notation is becoming more common every day. Many electronic pocket calculators use it to express numbers which otherwise would not fit into their displays. For example, an eight-digit calculator could not display the number 6 800 000 000.The decimal point would remain fixed on the right, and the 6 and the 8 would “overflow” to the left side. Such a number is often displayed as 6.8 09, which means 6.8 × 109. If you use a calculator which does not have scientific notation, we recommend that you express all numbers as powers of 10 before doing any arithmetic. Follow the rules in the last two examples, using your calculator to do arithmetic on the ordinary numbers. You should be able to add or subtract the powers of 10 in your head.
Computers also are prone to print results in scientific notation, and they use yet another minor modification. The printed number 2.3074 E-07 means 2.3074 × 10–7 for example. In this case the E indicates that the number following is an exponent of 10.
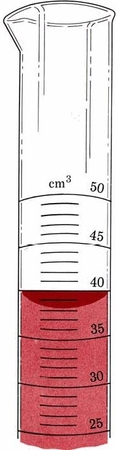
Figure \(\PageIndex{1}\) The level of a liquid in a graduated cylinder. The saucer-shaped surface of a liquid in a tube is called a meniscus.
Too Many Digits
Again in reference to our air-pollution experiment, we could express the mass of smoke collected as 3.42 × 10–2 g and the volume of the balloon as 1.021 926 4 × 107 cm3. There is something strange about the second quantity, though. It contains a number which was copied directly from the display of an electronic calculator and has too many digits.
The reliability of a quantity derived from a measurement is customarily indicated by the number of significant figures (or significant digits) it contains. For example, the three significant digits in the quantity 3.42 × 10–2 g tell us that a balance was used on which we could distinguish 3.42 × 10–2 g from 3.43 × 10–2 g or 3.41 × 10–2 g. There might be some question about the last digit, but those to the left of it are taken as completely reliable. Another way to indicate the same thing is (3.42±0.01) × 10–2 g. Our measurement is somewhere between 3.41 × 10–2 g and 3.43 × 10–2 g.
As another example of choosing an appropriate number of significant digits, let us read the volume of liquid in a graduated cylinder. The bottom of the meniscus lies between graduations corresponding to 38 and 39 cm3. We can estimate that it is at 38.5 cm3, but the last digit might be off a bit-perhaps it looks like 38.4 or 38.6 cm3 to you. Since the third digit is in question, we should use three significant figures. The volume would be recorded as 38.5 cm3. Laboratory equipment is often calibrated similarly to this graduated cylinder—you should estimate to the nearest tenth of the smallest graduation.
In some ordinary numbers, for example, 0.001 23, zeros serve merely to locate the decimal point. They do not indicate the reliability of the measurement and therefore are not significant. Another advantage of scientific notation is that we can assume that all digits are significant. Thus if 0.001 23 is written as 1.23 × 10–3, only the 1, 2, and 3, which indicate the reliability of the measurement, are written. The decimal point is located by the power of 10.
If the rule expressed in the previous paragraph is applied to the volume of air collected in our pollution experiment, 1.021 926 4 × 107 cm3, we find that the volume has eight significant digits. This implies that it was determined to ±1 cm3 out of about 10 million cm3, a reliability which corresponds to locating a grasshopper exactly at some point along the road from Philadelphia to New York City. For experiments as crude as ours, this is not likely. Let us see just how good the measurement was.
You will recall that we calculated the volume from the diameter of the balloon, 106 in. The three significant figures imply that this might have been as large as 107 in or as small as 105 in. We can repeat the calculation with each of these quantities to see how far off the volume would be:
\[\begin{equation} \begin{split} r &= \frac{1}{2} \times \text{107 in} = \text{53.5 in} \times \frac{\text{1 cm}}{\text{0.3937 in}} \\ \\ &=135.890 27 \text{cm} \end{split} \end{equation} \]
\[\begin{align} V &= \frac{4}{3} \times 3.141 59 \times (135.890 27)^3 \\ \\ &= 10 511 225 \text{cm}^3 = 1.051 122 5 \times 10^7 \text{cm}^3 \end{align} \]
or
\[\begin{align} V &= \frac{4}{3} \times 3.14159 \times \left( \frac{1}{2} \times \text{105 in} \frac{\text{1 cm}}{\text{0.3937 in}}\right)^3 \\ \\ &= 9 932 759 \text{cm}^3 = 0.993 275 9 \times 10^7 \text{cm}^3 \end{align} \]
That is, the volume is between 0.99 × 107 and 1.05 × 107 cm3 or (1.02 ± 0.03) × 107 cm3. We should round our result to three significant figures, for example, 1.02 cm³, because the last digit, namely 2, is in question.
Rules for Rounding Numbers
- All digits to be rounded are removed together, not one at a time.
- If the left-most digit to be removed is less than five, the last digit retained is not altered.
- If the left-most digit to be removed is greater than five, the last digit retained is increased by one.
- If the left-most digit to be removed is five and at least one of the other digits to be removed is nonzero. the last digit retained is increased by one.
- If the left-most digit to he removed is five and all other digits to he removed are zero, the last digit retained is not altered if it is even, but is increased by one if it is odd.
Application of the Rules for Rounding Numbers can be illustrated by an example.
Example \(\PageIndex{4}\) : Significant Figures
Round each of the numbers below to three significant figures.
- 34.7449
- 34.864
- 34.754
- 34.250
- 34.35
Solution:
a) Apply rules 1 and 2:
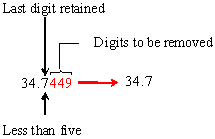
(Note that a different result would be obtained if the digits were incorrectly rounded one at a time from the right.)
b) Apply rules 1 and 3: 34.864 → 34.9
c) Apply rules 1 and 4: 34.754 → 34.8
d) Apply rules 1 and 5: 34.250 → 34.2
e) Apply rule 5: 34.35 → 34.4
To how many significant figures should we round our air-pollution results? We have already done a calculation involving multiplication and division to obtain the volume of our gas-collection balloon. It involved the following numbers:
| 106 | Three significant figures |
| 0.3937 | Four significant figures |
| 3.141 59 | Six significant figures (we could obtain more if we wanted) |
|
\(\frac{4}{3}\) and \(\frac{1}{2}\) |
An infinite number of significant figures since the integers in these fractions are exact by definition. Exact, or 'defined' numbers are not considered when calculating significant figures. |
The result of the calculation contained three significant figures — the same as the least-reliable number. This illustrates the general rule that for multiplication and division the number of significant figures in the result is the same as in the least-reliable measurement. Defined numbers such as π, ½ or 100 cm/1m are assumed to have an infinite number of significant figures.
In the case of addition and subtraction, a different rule applies. Suppose, for example, that we weighed a smoke-collection filter on a relatively inaccurate balance that could only be read to the nearest 0.01 g. After collecting a sample, the filter was reweighed on a single-pan balance to determine the mass of smoke particles.
Final mass: 2.3745 g (colored digits are in question)Initial mass: –2.32 g
Mass of smoke: 0.0545 g
Since the initial weighing could have been anywhere from 2.31 to 2.33 g, all three figures in the final result are in question. (It must be between 0.0445 and 0.0645 g). Thus there is but one significant digit, and the result is 0.05g. The rule here is that the result of addition or subtraction cannot contain more digits to the right than there are in any of the numbers added or subtracted. Note that subtraction can drastically reduce the number of significant digits when this rule is applied.
Rounding numbers is especially important if you use an electronic calculator, since these machines usually display a large number of digits, most of which are meaningless. The best procedure is to carry all digits to the end of the calculation (your calculator will not mind the extra work!) and then round appropriately. Answers to subsequent calculations in this book will be rounded according to the rules given. You may wish to go back to previous examples and round their answers correctly as well.
Example \(\PageIndex{5}\) : Rounding
Evaluate the following expressions, rounding the answer to the appropriate number of significant figures.
- \( \text{32.61 g} + \text{8.446 g} + \text{7.0 g} \)
- \( \text{0.136 cm}^3 \times \text{10.685 g cm}^{-3} \)
Solution
- \(\text{32.61 g} + \text{8.446 g} + \text{7.0 g} = \text{48.056 g} = \text{48.1g (7.0 has only one figure to the right of the decimal point.)} \)
- \( 0.136 \text{cm}^3 \times 10.685 \text{g cm}^{-3} = \text{1.453 g} = \text{1.45g (0.136 has only three significant figures.)} \)
When we suggested filling a surplus weather balloon to measure how much gas was pumped through our air-pollution collector, we mentioned that this would be a rather crude way to determine volume. For one thing, it would not be all that simple to measure the diameter of an 8- or 9-ft sphere reliably. Using a yardstick, we would be lucky to have successive measurements agree within half an inch or so. It was for this reason that the result was reported to the nearest inch. The degree to which repeated measurements of the same quantity yield the same result is called precision. Repetition of a highly precise measurement would yield almost identical results, whereas low precision implies numbers would differ by a significant percentage from each other.
A highly precise measurement of the diameter of our balloon could be achieved, but it would probably not be worthwhile. We have assumed a spherical shape, but this is almost certainly not exactly correct. No matter how precisely we determine the diameter, our measurement of gas volume will be influenced by deviations from the assumed shape. When one or more of our assumptions about a measuring instrument are wrong, the accuracy of a result will be affected. An obvious example would be a foot rule divided into 11 equal inches. Measurements employing this instrument might agree very precisely, but they would not be very accurate.
An important point of a different kind is illustrated in the last two paragraphs. A great many common words have been adopted into the language of science. Usually such an adoption is accompanied by an unambiguous scientific definition which does not appear in a normal dictionary. Precision and accuracy are many times treated as synonyms, but in science each has a slightly different meaning. Another example is quantity, which we have defined in terms of “number × unit.” Other English words like bulk, size, amount, and so forth, may be synonymous with quantity in everyday speech, but not in science. As you encounter other words like this, try to learn and use the scientific definition as soon as possible, and avoid confusing it with the other meanings you already know.
Even granting the crudeness of the measurements we have just described, they would be adequate to demonstrate whether or not an air-pollution problem existed. The next step would be to find a chemist or public health official who was an expert in assessing air quality, present your data, and convince that person to lend his or her skill and authority to your contention that something was wrong. Such a person would have available equipment whose precision and accuracy were adequate for highly reliable measurements and would be able to make authoritative public statements about the extent of the air-pollution problem.
Web Sources
Several sites were inspired by Charles Eames' "Powers of Ten" http://www.powersof10.com: http://www.wordwizz.com/pages/1uexp-13.htm http://micro.magnet.fsu.edu/primer/java/scienceopticsu/powersof10/index.html
Contributors
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.


