13.2: Collision Theory
- Last updated
- Save as PDF
- Page ID
- 204512
Collision energy
Consider two particles \(A\) and \(B\) in a system. The kinetic energy of these two particles is
\[K_{AB} = \dfrac{\textbf{p}_A^2}{2m_A} + \dfrac{\textbf{p}_B^2}{2m_B} \label{27.6.1} \]
We can describe kinetic energy in terms of center-of-mass \(\left( \textbf{P} \right)\) and relative momentum \(\left( \textbf{p} \right)\), which are given by
\(\textbf{P} = \textbf{p}_A + \textbf{p}_B\)
and
\[ \begin{align*} \textbf{p} &= \text{relative velocity}\times \mu \\[4pt] &= (\textbf{v}_A -\textbf{v}_B) \times \left(\dfrac{m_A m_B}{m_A + m_B}\right) \\[4pt] &= \dfrac{m_B \textbf{p}_A - m_A \textbf{p}_B}{M}\end{align*} \nonumber \]
where
\(M = m_A + m_B\)
is the total mass of the two particles, and
\[\mu = \dfrac{m_A m_B}{M} \nonumber \]
is the reduced mass of the two particles.
Substituting these terms into equation \(\ref{27.6.1}\), we find
\[K_{AB} = \dfrac{\textbf{p}_A^2}{2m_A} + \dfrac{\textbf{p}_B^2}{2m_B} = \dfrac{\textbf{P}^2}{2M} + \dfrac{\textbf{p}^2}{2 \mu} \nonumber \]
Note that the kinetic energy separates into a sum of a center-of-mass term and a relative momentum term.
Now the relative position of the two particles is \(\textbf{r} = \textbf{r}_A - \textbf{r}_B\) so that the relative velocity is \(\dot{\textbf{r}} = \dot{\textbf{r}}_A - \dot{\textbf{r}}_B\) or \(\textbf{v} = \textbf{v}_A - \textbf{v}_B\). Thus, if the two particles are approaching each other such that \(\textbf{v}_A = - \textbf{v}_B\), then \(\textbf{v} = 2 \textbf{v}_A\). However, by equipartitioning the relative kinetic energy, which is mass independent, we get
\[\left< \dfrac{\textbf{p}^2}{2 \mu} \right> = \dfrac{3}{2} k_B T \nonumber \]
which is called the collision energy
Collision cross-section
Consider two molecules in a system. The probability that they will collide increases with the effective “size” of each particle. However, the size measure that is relevant is the apparent cross-section area of each particle. For simplicity, suppose the particles are spherical, which is not a bad approximation for small molecules. If we are looking at a sphere, what we perceive as the size of the sphere is the cross section area of a great circle. Recall that each spherical particle has an associated “collision sphere” that just encloses two particles at closest contact, i.e., at the moment of a collision, and that this sphere is a radius \(d\), where \(d\) is the diameter of each spherical particle. The cross-section of this collision sphere represents an effective cross section for each particle inside which a collision is imminent. The cross-section of the collision sphere is the area of a great circle, which is \(\pi d^2\). We denote this apparent cross section area \(\sigma\). Thus, for spherical particles \(A\) and \(B\) with diameters \(d_A\) and \(d_B\), the individual cross sections are
\[\sigma_A = \pi d_A^2, \: \: \: \sigma_B = \pi d_B^2 \nonumber \]
The collision cross section, \(\sigma_{AB}\) is determined by an effective diameter \(d_{AB}\) characteristic of both particles. The collision probability increases of both particles have large diameters and decreases if one of them has a smaller diameter than the other. Hence, a simple measure sensitive to this is the arithmetic average
\[d_{AB} = \dfrac{1}{2} \left( d_A + d_B \right) \nonumber \]
and the resulting collision cross section becomes
\[\begin{align} \sigma_{AB} &= \pi d_{AB}^2 \nonumber\\ &= \pi \left( \dfrac{d_A + d_B}{2} \right)^2 \nonumber\\ &= \dfrac{\pi}{4} \left( d_A^2 + 2d_A d_B + d_B^2 \right) \nonumber \\ &= \dfrac{1}{4} \left( \sigma_A + 2 \sqrt{\sigma_A \sigma_B} + \sigma_B \right) \nonumber\\ &= \dfrac{1}{2} \left[ \left( \dfrac{\sigma_A + \sigma_B}{2} \right) + \sqrt{\sigma_A \sigma_B} \right] \nonumber \end{align} \nonumber \]
which, interestingly, is an average of the two types of averages of the two individual cross sections, the arithmetic and geometric averages!
Average collision Frequency
Consider a system of particles with individual cross sections \(\sigma\). A particle of cross section \(\sigma\) that moves a distance \(l\) in a time \(\Delta t\) will sweep out a cylindrical volume (ignoring the spherical caps) of volume \(\sigma l\) (Figure 27.6.1 ). If the system has a number density \(\rho\), then the number of collisions that will occur is
\[N_{\text{coll}} = \rho \sigma l \nonumber \]
We define the collision frequency for a single molecule, \(z_A\), also known as the average collision rate as \(N_{\text{coll}}/ \Delta t\), i.e.,
\[z_A = \dfrac{N_{\text{coll}}}{\Delta t} = \dfrac{\rho \sigma l}{\Delta t} = \rho \sigma \langle v \rangle \label{27.6.2} \]
where \(\langle v \rangle\) is the average speed of a particle
\[\langle v \rangle = \sqrt{\dfrac{8 k_B T}{\pi m_A}} \nonumber \]
Equation \(\ref{27.6.2}\) is not quite correct because it is based on the assumption that only the molecule of interest is moving. If we take into account the fact that all of the particles are moving relative to one another, and assume that all of the particles are of the same type (say, type \(A\)), then performing the average over a Maxwell-Boltzmann speed distribution gives
\[\langle v_r \rangle = \sqrt{\dfrac{8 k_B T}{\pi \mu}} \nonumber \]
where \(\mu = m_A/2\) is the reduced mass.
Thus,
\[\langle v_r \rangle = \sqrt{2} \langle v \rangle \nonumber \]
and
\[z_A = \sqrt{2} \rho \sigma \langle v \rangle\ = \rho \sigma \langle v_r \rangle \nonumber \]
The reciprocal of \(z_A\) is a measure of the average time between collisions for a single molecule.
Mean Free Path
The mean free path is the distance a particle will travel, on average, before experiencing a collision event. This is defined as the product of the average speed of a particle and the time between collisions. The former is \(\langle v \rangle \), while the latter is \(1/z_A\). Hence, we have
\[\lambda = \dfrac{\langle v\rangle}{\sqrt{2} \rho \sigma \langle v \rangle} = \dfrac{1}{\sqrt{2} \rho \sigma} \nonumber \]
The mean free path can also be described using terms from the ideal gas law, because \(\rho = \dfrac{P \cdot N_A}{R \cdot T}\):
\[\lambda = \dfrac {R \cdot T}{\sqrt{2} \cdot N_A \cdot \sigma \cdot P} \nonumber \]
Random Walks
In any system, a particle undergoing frequent collisions will have the direction of its motion changed with each collision and will trace out a path that appears to be random. In fact, if we treat the process as statistical, then, we are, in fact, treating each collision event as a random event, and the particle will change its direction at random times in random ways! Such a path might appear as shown in Figure \(\PageIndex{2}\). Such a path is often referred to as a random walk path.
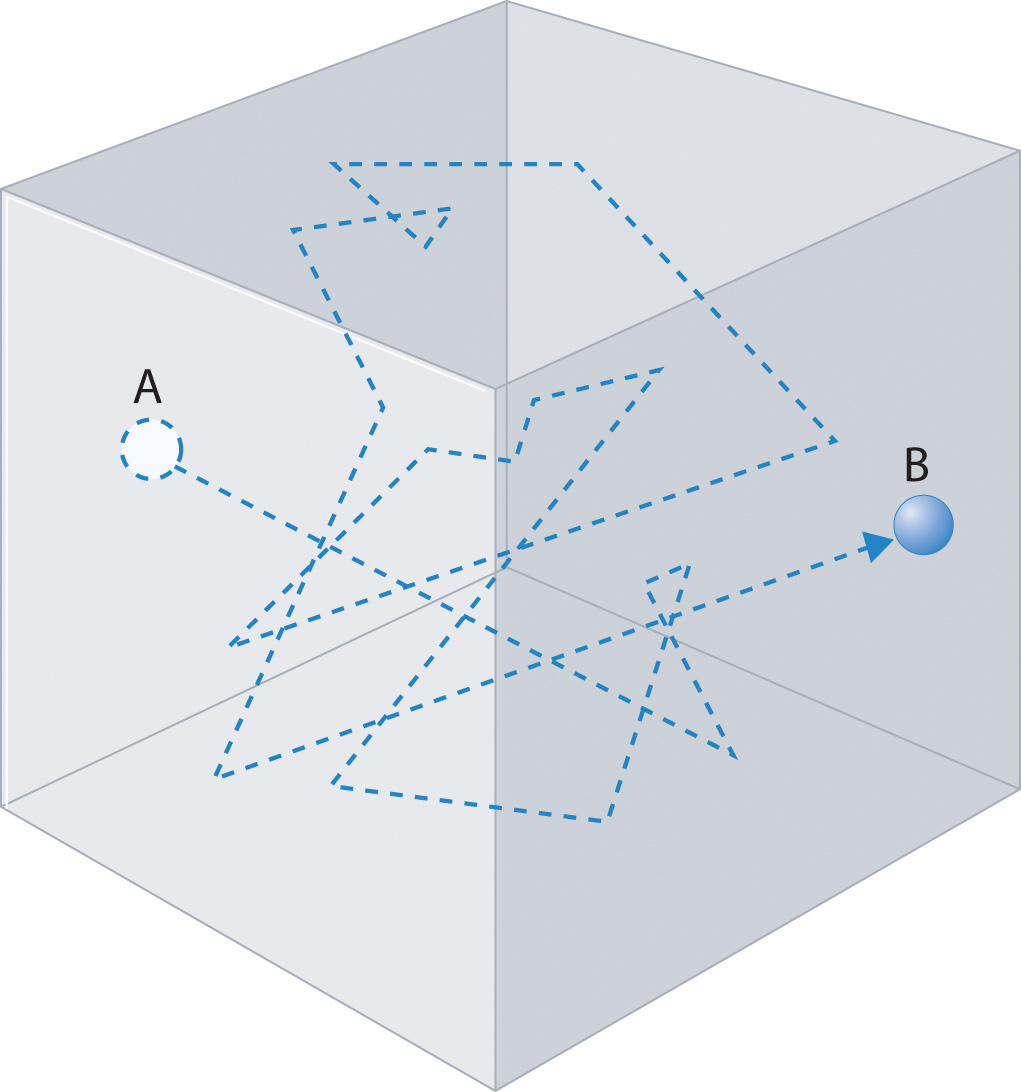
In order to analyze such paths, let us consider a random walk in one dimension. We’ll assume that the particle move a mean-free path length \(\lambda\) between collisions and that each collision changes the direction of the particles motion, which in one dimension, means that the particle moves either to the right or to the left after each event. This can be mapped onto a metaphoric “coin toss” that can come up heads “H” or tails “T”, with “H” causing motion to the right, and “T” causing motion to the left. Let there be \(N\) such coin tosses, let \(i\) be the number of times “H” comes up and \(j\) denote the number of times “T” comes up. Thus, the progress of the particle, which we define as net motion to the right, is given by \((i - j) \lambda\). Letting \(k = i - j\), this is just \(k \lambda\). Thus, we need to know what the probability is for obtaining a particular value of \(k\) in a very large number \(N\) of coin tosses. Denote this \(P(k)\).
In \(N\) coin tosses, the total number of possible sequences of “H” and “T” is \(2^N\). However, the number of ways we can obtain \(i\) heads and \)j\) tails, with \(i + j = N\) is a binomial coefficient \(N!/i!j!\). Now
\[j = N - i = N - (j + k) = N - j - k \nonumber \]
so that \(j = (N - k )/2\). Similarly,
\[i = N - j = N - (i - k) = N - i + k \nonumber \]
so that \(i = (N + k)/2\). Thus, the probability \(P(k)\) is
\[P(k) = \dfrac{N!}{2^N i! j!} = \dfrac{1}{2^N} \dfrac{N!}{\left(\dfrac{N + k}{2} \right) ! \left( \dfrac{N - k}{2} \right) !} \nonumber \]
We now take the logarithm of both sides:
\[\text{ln} \: P(k) = \: \text{ln} \: N! - \: \text{ln} \: 2^N - \: \text{ln} \: \left( \dfrac{N + k}{2} \right) ! - \: \text{ln} \: \left( \dfrac{N - k}{2} \right) ! \nonumber \]
and use Stirling’s approximation:
\[\text{ln} \: N! \approx N \: \text{ln} \: N - N \nonumber \]
and write \(\text{ln} \: P(k)\) as
\[\begin{align} \text{ln} \: P(k) &\approx N \: \text{ln} \: N - N - N \: \text{ln} \: 2 - \dfrac{1}{2} (N + k) \: \text{ln} \: \dfrac{1}{2} (N + k) + \dfrac{1}{2} (N + k) - \dfrac{1}{2} (N - k) \: \text{ln} \: \dfrac{1}{2} (N - k) + \dfrac{1}{2} (N - k) \nonumber\\ &= N \: \text{ln} \: N - N \: \text{ln} \: 2 + \dfrac{1}{2} (N + k) \: \text{ln} \: \dfrac{1}{2} - \dfrac{1}{2} (N + k) \: \text{ln} \: (N + k) - \dfrac{1}{2} (N - k) \: \text{ln} \: \dfrac{1}{2} - \dfrac{1}{2} (N - k) \: \text{ln} \: (N - k) \nonumber\\ &= N \: \text{ln} \: N - N \: \text{ln} \: 2 + \dfrac{1}{2} (N + k) \: \text{ln} \: 2 - \dfrac{1}{2} (N + k) \: \text{ln} \: (N + k) + \dfrac{1}{2} (N - k) \: \text{ln} \: 2 - \dfrac{1}{2} (N - k) \: \text{ln} \: (N - k) \nonumber\\ &= N \: \text{ln} \: N - \dfrac{1}{2} \left[ (N + k) \: \text{ln} \: (N + k) + (N - k) \: \text{ln} \: (N - k) \right] \nonumber\end{align} \nonumber \]
Now, write
\[\text{ln} \: (N + k) = \: \text{ln} \: N \left( 1 + \dfrac{k}{N} \right) = \: \text{ln} \: N + \: \text{ln} \: \left( 1 + \dfrac{k}{N} \right) \nonumber \]
and
\[\text{ln} \: (N - k) = \: \text{ln} \: N \left( 1 - \dfrac{k}{N} \right) = \: \text{ln} \: N + \: \text{ln} \: \left( 1 - \dfrac{k}{N} \right) \nonumber \]
We now use the expansions
\[\begin{align} \text{ln} \: \left( 1 + \dfrac{k}{N} \right) &= \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 + \cdots \nonumber \\ \text{ln} \: \left( 1 - \dfrac{k}{N} \right) &= - \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 + \cdots \nonumber\end{align} \nonumber \]
If we stop at the second-order term, then
\[\begin{align} \text{ln} \: P(k) &= N \: \text{ln} \: N - \dfrac{1}{2} (N + k) \left[ \: \text{ln} \: N + \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 \right] - \dfrac{1}{2} (N - k) \left[ \: \text{ln} \: N - \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 \right] \nonumber \\ &= -\dfrac{1}{2} (N + k) \left[ \left( \dfrac{k}{N} \right) - \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 \right] + \dfrac{1}{2} (N - k) \left[ \left( \dfrac{k}{N} \right) + \dfrac{1}{2} \left( \dfrac{k}{N} \right)^2 \right] \nonumber \\ &= \dfrac{1}{2} N \left( \dfrac{k}{N} \right)^2 - k \left( \dfrac{k}{N} \right) \nonumber\\ & = \dfrac{k^2}{2N} - \dfrac{k^2}{N} = - \dfrac{k^2}{2N} \nonumber\end{align} \nonumber \]
so that
\[P(k) = e^{-k^2/2N} \nonumber \]
Now, if we let \(x = k \lambda\) and \(L = \sqrt{N} \lambda\), and if we let \(x\) be a continuous random variable, then the corresponding probability distribution \(P(x)\) becomes
\[P(x) = \dfrac{1}{L \sqrt{2 \pi}} \: e^{-x^2/2L^2} = \dfrac{1}{\sqrt{2 \pi N \lambda^2}} \: e^{-x^2/2N \lambda^2} \label{27.6.3} \]
which is a simple Gaussian distribution. Now, \(N\) is the number of collisions, which is given by \(z_At\), so we can write the probability distribution for the particle to diffuse a distance \(x\) in time \(t\) as
\[P(x, t) = \dfrac{1}{\sqrt{2 \pi z_At \lambda^2}} \: e^{-x^2/2z_At \lambda^2} \nonumber \]
Define \(D = z_A \lambda^2/2\) as the diffusion constant, which has units of (length)\(^{\text{2}}\)/time. The distribution then becomes
\[P(x, t) = \dfrac{1}{\sqrt{4 \pi D t }} \: e^{-x^2/4D t} \nonumber \]
Note that this distribution satisfies the following equation:
\[\dfrac{\partial}{\partial t} P(x, t) = D \dfrac{\partial^2}{\partial x^2} P(x, t) \nonumber \]
which is called the diffusion equation. The diffusion equation is, in fact, more general than the Gaussian distribution in Equation \(\ref{27.6.3}\). It is capable of predicting the distribution in any one-dimensional geometry subject to any initial distribution \(P(x, 0)\) and any imposed boundary conditions.
In three dimensions, we consider the three spatial directions to be independent, hence, the probability distribution for a particle to diffuse to a location \(\textbf{r} = (x, y, z)\) is just a product of the three one-dimensional distributions:
\[\mathcal{P}(\textbf{r}) = P(x) \: P(y) \: P(z) = \dfrac{1}{(4 \pi D t) ^{3/2}} \: e^{-\left( x^2 + y^2 + z^2 \right)/4Dt} \nonumber \]
and if we are only interested in diffusion over a distance \(r\), we can introduce spherical coordinates, integrate over the angles, and we find that
\[P(r, t) = \dfrac{4 \pi}{(4 \pi D t)^{3/2}} \: e^{-r^2/4Dt} \nonumber \]
Total collision frequency per unit volume
In equation 27.6.18, \(z_A\) represents the collision frequency for one specific molecule in a gas sample. If we wish to calculate the total collision frequency per unit volume, the number density of the molecules, \(\rho\), must be taken into account. The total collision frequency in a sample that contains only A molecules, \(Z_{AA}\), is
\[Z_{AA} = \dfrac{1}{2}\rho z_A = \dfrac{1}{2} \sigma \langle v_r \rangle \rho^2 = \dfrac{\sigma \langle v\rangle \rho^2}{\sqrt{2}}\nonumber \]
The factor of \(\dfrac {1}{2}\) must be included to avoid double counting collisions between similar molecules. (This is identical reasoning to the fact that there is only one way to roll double 3 with two dice.)
If you have a gas sample that contains A molecules and B molecules, then
\[Z_{AB} = \sigma_{AB} \langle v_r \rangle \rho_A \rho_B \label{27.6.4} \]
where
\(\sigma_{AB} = \pi \left (\dfrac{d_A + d_B}{2} \right)^2 \) and \(\langle v_r \rangle = \sqrt{\dfrac{8 k_B T}{\pi \mu}} \nonumber\)
Example \(\PageIndex{1}\)
Calculate the frequency of hydrogen-hydrogen collisions in a 1.00 cubic centimeter container at 1.00 bar and 298 K.
Solution
The collisional frquency requires knowledge of (1) the number denisty, the average speed (Equation \ref{27.6.4}).
The value of \(\sigma_{H_2}\) is 2.30 x 10-19 m2.
The number density:
\[\rho = \left(\dfrac{N_AP_{H_2}}{RT} \right) = \left(\dfrac{(6.022x10^{23} mole^{-1})(1.00 ~\text{bar})}{(0.08314 L·bar·mol^{-1}·K^{-1})(298 K)} \right) = 2.43 \times 10^{22} L^{-1} = 2.43 \times 10^{25} m^{-3} \]
The average speed:
\[\langle \text v\rangle = \sqrt{\dfrac{8 \text{R T}}{\pi \text{M}}} = \sqrt{\left(\dfrac{8(8.314 J·K^{-1})(298 K)}{\pi(0.002016 kg)}\right)} = 1770 \dfrac{m}{s}\]
These are substituted into Equation \ref{27.6.4} to get the collisional frequency
\[ \begin{align*} Z_{H_2,H_2} &= \dfrac{(2.30 x 10^{-19}m^2)(1770 \dfrac{m}{s})(2.43 x 10^{25} m^{-3})^2}{\sqrt{2}} \\[4pt] &= 1.7 x 10^{35} s^{-1}m^{-3} \\[4pt] &= 1.7 \times 10^{29} s^{-1}cm^{-3} \end{align*}\]

