12.5: The Van't Hoff Equation
- Page ID
- 204509
We can use Gibbs-Helmholtz to get the temperature dependence of \(K\)
\[ \left( \dfrac{∂[Δ_rG^o/T]}{∂T} \right)_P = \dfrac{-Δ_rH^o}{T^2}\]
At equilibrium, we can equate \(Δ_rG^o\) to \(-RT\ln K\) so we get:
\[ \left( \dfrac{∂[lnK]}{∂T} \right)_P = \dfrac{Δ_rH^o}{RT^2} \]
We see that whether \(K\) increases or decreases with temperature is linked to whether the reaction enthalpy is positive or negative. If temperature is changed little enough that \(Δ_rH^o\) can be considered constant, we can translate a \(K\) value at one temperature into another by integrating the above expression, we get a similar derivation as with melting point depression:
\[\ln \dfrac{K(T_2}{K(T_1)} = \dfrac{-Δ_rH^o}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_1} \right)\]
If more precision is required we could correct for the temperature changes of ΔrHo by using heat capacity data.
How \(K\) increases or decreases with temperature is linked to whether the reaction enthalpy is positive or negative.
The expression for \(K\) is a rather sensitive function of temperature given its exponential dependence on the difference of stoichiometric coefficients One way to see the sensitive temperature dependence of equilibrium constants is to recall that
\[K=e^{−\Delta_r{G^o}/RT}\label{18}\]
However, since under constant pressure and temperature
\[\Delta_r{G^o}= \Delta_r{H^o}−T\Delta_r{S^o}\]
Equation \(\ref{18}\) becomes
\[ K=e^{-\Delta_r{H^o}/RT} e^{\Delta_r{S^o}/R}\label{19}\]
Taking the natural log of both sides, we obtain a linear relation between \(\ln K \)and the standard enthalpies and entropies:
\[\ln K = - \dfrac{\Delta_r{H^o}}{R} \dfrac{1}{T} + \dfrac{\Delta_r{S^o}}{R}\label{20}\]
which is known as the van’t Hoff equation. It shows that a plot of \(\ln K\) vs. \(1/T\) should be a line with slope \(-\Delta_r{H^o}/R\) and intercept \(\Delta_r{S^o}/R\).
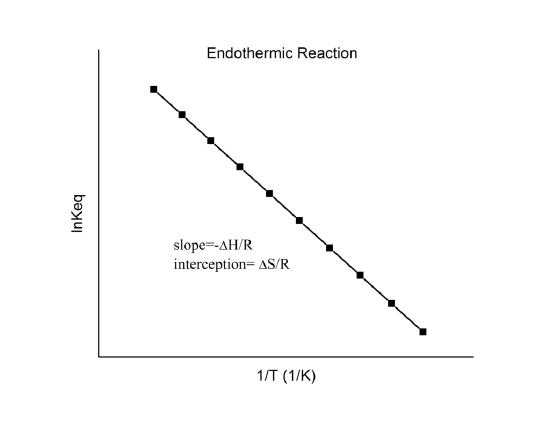
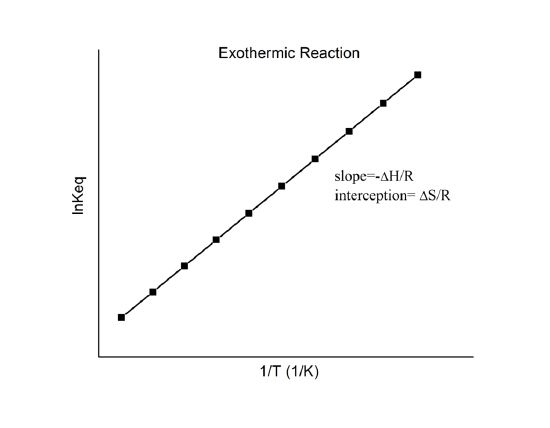
Hence, these quantities can be determined from the \(\ln K\) vs. \(1/T\) data without doing calorimetry. Of course, the main assumption here is that \(\Delta_r{H^o}\) and \(\Delta_r{S^o}\) are only very weakly dependent on \(T\), which is usually valid.

