3.3 Chemical Bonds

Skills to Develop

• To quantitatively describe the energetic factors involved in the formation of an ionic bond.

Chemical bonds form when electrons can be simultaneously close to two or more nuclei, but beyond this, there is no simple, easily understood theory that would not only explain why atoms bind together to form molecules, but would also predict the three-dimensional structures of the resulting compounds as well as the energies and other properties of the bonds themselves. Unfortunately, no one theory exists that accomplishes these goals in a satisfactory way for all of the many categories of compounds that are known. Moreover, it seems likely that if such a theory does ever come into being, it will be far from simple.

When we are faced with a scientific problem of this complexity, experience has shown that it is often more useful to concentrate instead on developing models. A scientific model is something like a theory in that it should be able to explain observed phenomena and to make useful predictions. But whereas a theory can be discredited by a single contradictory case, a model can be useful even if it does not encompass all instances of the phenomena it attempts to explain. We do not even require that a model be a credible representation of reality; all we ask is that be able to explain the behavior of those cases to which it is applicable in terms that are consistent with the model itself. An example of a model that you may already know about is the kinetic molecular theory of gases. Despite its name, this is really a model (at least at the level that beginning students use it) because it does not even try to explain the observed behavior of real gases. Nevertheless, it serves as a tool for developing our understanding of gases, and as a starting point for more elaborate treatments.Given the extraordinary variety of ways in which atoms combine into aggregates, it should come as no surprise that a number of useful bonding models have been developed. Most of them apply only to certain classes of compounds, or attempt to explain only a restricted range of phenomena. In this section we will provide brief descriptions of some of the bonding models; the more important of these will be treated in much more detail in later parts of this chapter.

Ionic Bonding

Ever since the discovery early in the 19th century that solutions of salts and other electrolytes conduct electric current, there has been general agreement that the forces that hold atoms together must be electrical in nature. Electrolytic solutions contain ions having opposite electrical charges, opposite charges attract, so perhaps the substances from which these ions come consist of positive and negatively charged atoms held together by electrostatic attraction.

It turns out that this is not true generally, but a model built on this assumption does a fairly good job of explaining a rather small but important class of compounds that are called ionic solids. The most well known example of such a compound is sodium chloride, which consists of two interpenetrating lattices of Na⁺ and Cl^– ions arranged in such as way that every ion of one type is surrounded (in three dimensional space) by six ions of opposite charge. The main limitation of this model is that it applies really well only to the small class of solids composed of Group 1 and 2 elements with highly electronegative elements such as the halogens.

According to the ionic electrostatic model, solids such as NaCl consist of positive and negative ions arranged in a crystal lattice. Each ion is attracted to neighboring ions of opposite charge, and is repelled by ions of like charge; this combination of attractions and repulsions, acting in all directions, causes the ion to be tightly fixed in its own location in the crystal lattice.

Ions are atoms or molecules which are electrically charged. Cations are positively charged and anions carry a negative charge. Ions form when atoms gain or lose electrons. Since electrons are negatively charged, an atom that loses one or more electrons will become positively charged; an atom that gains one or more electrons becomes negatively charged. Ionic bonding is the attraction between positively- and negatively-charged ions. These oppositely charged ions attract each other to form ionic networks (or lattices). Electrostatics explains why this happens: opposite charges attract and like charges repel. When many ions attract each other, they form large, ordered, crystal lattices in which each ion is surrounded by ions of the opposite charge. Generally, when metals react with non-metals, electrons are transferred from the metals to the non-metals. The metals form positively-charged ions and the non-metals form negatively-charged ions.

Ionic bonds form when metals and non-metals chemically react. By definition, a metal is relatively stable if it loses electrons to form a complete valence shell and becomes positively charged. Likewise, a non-metal becomes stable by gaining electrons to complete its valence shell and become negatively charged. When metals and non-metals react, the metals lose electrons by transferring them to the non-metals, which gain them. Consequently, ions are formed, which instantly attract each other—ionic bonding.

Example \(\PageIndex{1}\): Sodium Chloride

For example, in the reaction of Na (sodium) and Cl (chlorine), each Cl atom takes one electron from a Na atom. Therefore each Na becomes a Na⁺ cation and each Cl atom becomes a Cl^- anion. Due to their opposite charges, they attract each other to form an ionic lattice. The formula (ratio of positive to negative ions) in the lattice is NaCl.

\[2Na_{(s)} + Cl_{2(g)} \rightarrow 2NaCl_{(s)}\]

These ions are arranged in solid NaCl in a regular three-dimensional arrangement (or lattice):

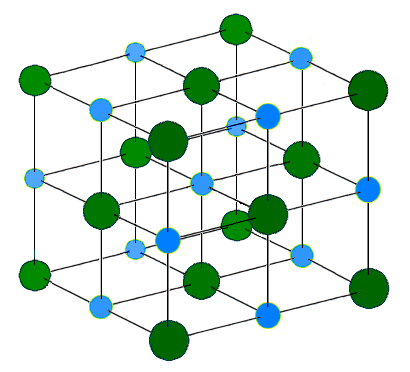
NaCl lattice. (left) 3-D structure and (right) simple 2D slice through lattes. Images used with permission from Wikipedia and Mike Blaber.

The chlorine has a high affinity for electrons, and the sodium has a low ionization potential. Thus the chlorine gains an electron from the sodium atom. This can be represented using electron-dot symbols (here we will consider one chlorine atom, rather than Cl₂):

The arrow indicates the transfer of the electron from sodium to chlorine to form the Na⁺ metal ion and the Cl^- chloride ion. Each ion now has an octet of electrons in its valence shell.

Covalent Bonding

Formation of an ionic bond by complete transfer of an electron from one atom to another is possible only for a fairly restricted set of elements. Covalent bonding, in which neither atom loses complete control over its valence electrons, is much more common. In a covalent bond the electrons occupy a region of space between the two nuclei and are said to be shared by them. This model originated with the theory developed by G.N. Lewis in 1916, and it remains the most widely-used model of chemical bonding. The essential element s of this model can best be understood by examining the simplest possible molecule. This is the hydrogen molecule ion H₂⁺, which consists of two nuclei and one electron. First, however, think what would happen if we tried to make the even simpler molecule H₂²⁺. Since this would consist only of two protons whose electrostatic charges would repel each other at all distances, it is clear that such a molecule cannot exist; something more than two nuclei are required for bonding to occur.

In the hydrogen molecule ion H₂⁺ we have a third particle, an electron. The effect of this electron will depend on its location with respect to the two nuclei. If the electron is in the space between the two nuclei, it will attract both protons toward itself, and thus toward each other. If the total attraction energy exceeds the internuclear repulsion, there will be a net bonding effect and the molecule will be stable. If, on the other hand, the electron is off to one side, it will attract both nuclei, but it will attract the closer one much more strongly, owing to the inverse-square nature of Coulomb's law. As a consequence, the electron will now help the electrostatic repulsion to push the two nuclei apart.

We see, then, that the electron is an essential component of a chemical bond, but that it must be in the right place: between the two nuclei. Coulomb's law can be used to calculate the forces experienced by the two nuclei for various positions of the electron, but we have been vague in our language about the actual nature of the chemical bonds themselves. We know that a covalent bond involves the ‘sharing’ of a pair of electrons between two atoms - but how does this happen, and how does it lead to the formation of a bond holding the two atoms together?

The valence bond theory is introduced to describe bonding in covalent molecules. In this model, bonds are considered to form from the overlapping of two atomic orbitals on different atoms, each orbital containing a single electron. In looking at simple inorganic molecules such as H₂ or HF, our present understanding of s and p atomic orbitals will suffice. To explain the bonding in more complex molecules, however, we will need to introduce the concept of hybrid orbitals.

Example: The H₂ molecule

The simplest case to consider is the hydrogen molecule, H₂. When we say that the two electrons from each of the hydrogen atoms are shared to form a covalent bond between the two atoms, what we mean in valence bond theory terms is that the two spherical 1s orbitals overlap, allowing the two electrons to form a pair within the two overlapping orbitals. In simple terms, we can say that both electrons now spend more time between the two nuclei and thus hold the atoms together. As we will see, the situation is not quite so simple as that, because the electron pair must still obey quantum mechanics - that is, the two electrons must now occupy a shared orbital space. This will be the essential principle of valence bond theory.

These two electrons are now attracted to the positive charge of both of the hydrogen nuclei, with the result that they serve as a sort of ‘chemical glue’ holding the two nuclei together.

How far apart are the two nuclei? That is a very important issue to consider. If they are too far apart, their respective 1s orbitals cannot overlap, and thus no covalent bond can form - they are still just two separate hydrogen atoms. As they move closer and closer together, orbital overlap begins to occur, and a bond begins to form. This lowers the potential energy of the system, as new, attractive positive-negative electrostatic interactions become possible between the nucleus of one atom and the electron of the second. However, something else is happening at the same time: as the atoms get closer, the repulsive positive-positive interaction between the two nuclei also begins to increase.

At first this repulsion is more than offset by the attraction between nuclei and electrons, but at a certain point, as the nuclei get even closer, the repulsive forces begin to overcome the attractive forces, and the potential energy of the system rises quickly. When the two nuclei are ‘too close’, we have a very unstable, high-energy situation. There is a defined optimal distance between the nuclei in which the potential energy is at a minimum, meaning that the combined attractive and repulsive forces add up to the greatest overall attractive force. This optimal internuclear distance is the bond length. For the H₂ molecule, this distance is 74 x 10^-12 meters, or 0.74 Å (Å means angstrom, or 10^-10 meters). Likewise, the difference in potential energy between the lowest state (at the optimal internuclear distance) and the state where the two atoms are completely separated is called the bond energy. For the hydrogen molecule, this energy is equal to about 104 kcal/mol.

Every covalent bond in a given molecule has a characteristic length and strength. In general, carbon-carbon single bonds are about 1.5 Å long (Å means angstrom, or 10^-10 meters) while carbon-carbon double bonds are about 1.3 Å, carbon-oxygen double bonds are about 1.2 Å, and carbon-hydrogen bonds are in the range of 1.0 – 1.1 Å. Most covalent bonds range in strength from just under 100 kcal/mole (for a carbon-hydrogen bond in ethane, for example) up to nearly 200 kcal/mole.

Orbital Overlap: A Second Look

You learned that as two hydrogen atoms approach each other from an infinite distance, the energy of the system reaches a minimum. This region of minimum energy in the energy diagram corresponds to the formation of a covalent bond between the two atoms at an H–H distance of 74 pm. According to quantum mechanics, bonds form between atoms because their atomic orbitals overlap, with each region of overlap accommodating a maximum of two electrons with opposite spin, in accordance with the Pauli principle. In this case, a bond forms between the two hydrogen atoms when the singly occupied 1s atomic orbital of one hydrogen atom overlaps with the singly occupied 1s atomic orbital of a second hydrogen atom. Electron density between the nuclei is increased because of this orbital overlap and results in a localized electron-pair bond. When the orbitals of two atoms overlap along the line between the two atomic nuclei (the internuclear axis), the bond is designated as a sigma (\( \sigma \) ) bond. The formation of a sigma bond between two H atoms is shown here:

1

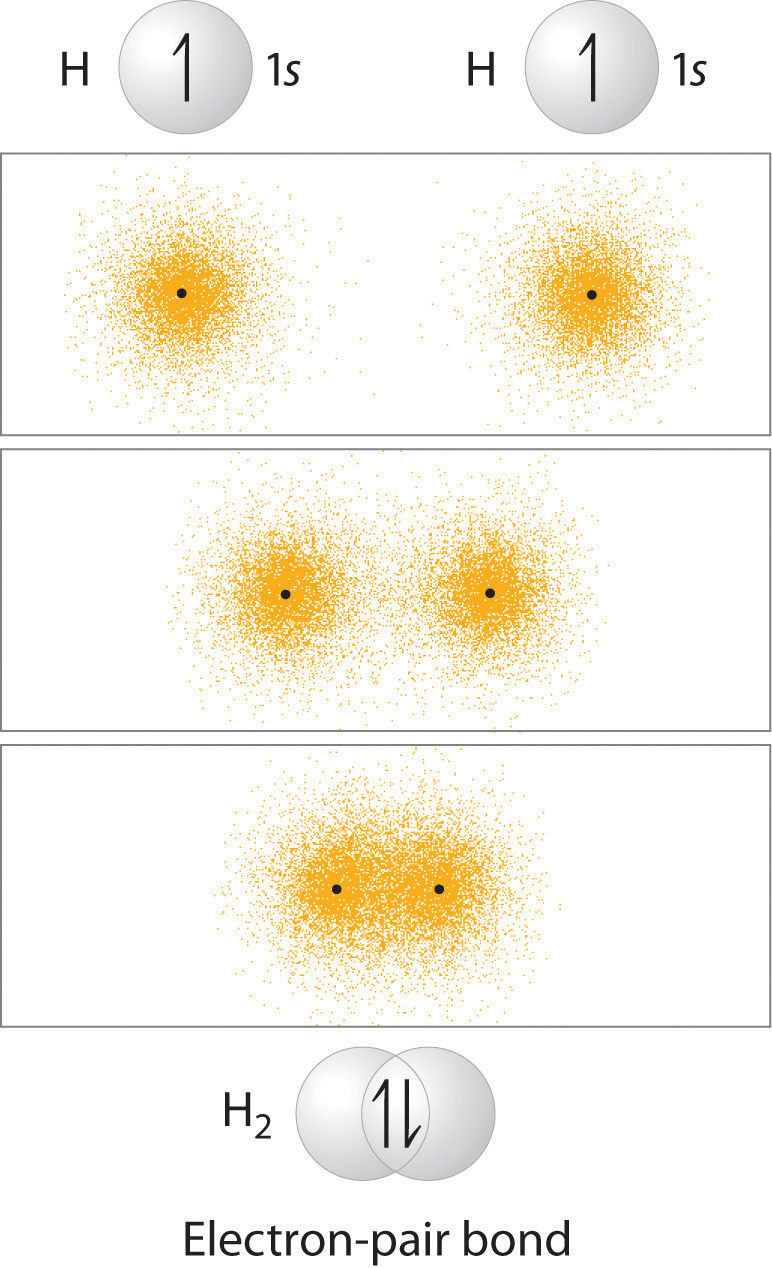
Overlap of Two Singly Occupied Hydrogen 1s Atomic Orbitals Produces an H–H Bond in H_2. The formation of H₂ from two hydrogen atoms, each with a single electron in a 1s orbital, occurs as the electrons are shared to form an electron-pair bond, as indicated schematically by the gray spheres and black arrows. The orange electron density distributions show that the formation of an H₂ molecule increases the electron density in the region between the two positively charged nuclei.

All orbitals other than s orbitals are able to form a second type of covalent bond, based on their ability to overlap, simultaneously, both above and below the internuclear axis of the two bonding atoms. This type of overlap is called a pi (\(pi \)) bond.

There are two basic assumptions for covalent bonding theory:

1. The strength of a covalent bond is proportional to the amount of overlap between atomic orbitals; that is, the greater the overlap, the more stable the bond. Sigma bonds are generally stronger than pi bonds because the overlap is greater in sigma bonds than in pi bonds.
2. An atom can use different combinations of atomic orbitals to maximize the overlap of orbitals used by bonded atoms. (Described later when we discuss hybrid orbitals.)

Sigma Bond Overlapping

The figure below shows a sigma bond formed by the overlap of two s atomic orbitals, two p atomic orbitals, and an s and an p orbital. Notice that bonding overlap occurs when the interacting atomic orbitals have the correct orientation (are "pointing at" each other).

Maximum overlap occurs between orbitals with the same spatial orientation and similar energies.

2

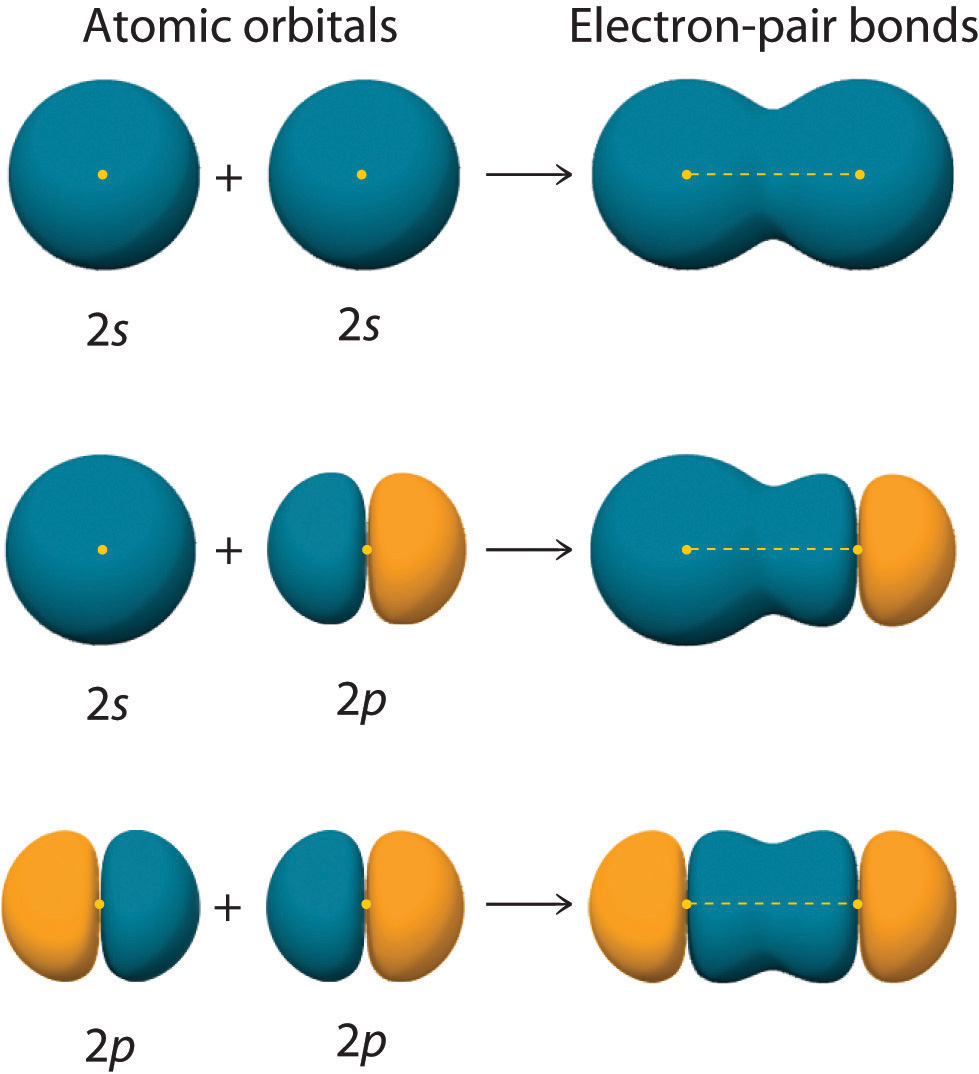
Three Different Ways to Form an Electron-Pair Bond. An electron-pair bond can be formed by the overlap of any of the following combinations of two singly occupied atomic orbitals: two s atomic orbitals (a), an s and an p atomic orbital (b), and two p atomic orbitals (c).

Pi Bond Overlapping

The figure below shows a pi bond formed by the overlap of two p atomic orbitals, and a p and a d orbital. Notice that bonding overlap occurs when the interacting atomic orbitals have the correct orientation (are "parallel" with each other).

A pi bond (π bond) is a type of covalent bond that results from the side-by-side overlap of two p orbitals, as illustrated in the figure below. In a π bond, the regions of orbital overlap lie above and below the internuclear axis. Along the axis itself, there is a node, that is, a plane with no probability of finding an electron.

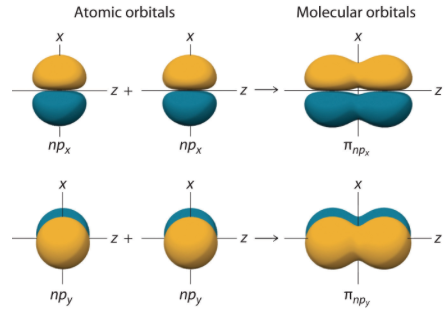
Formation of π Molecular Orbitals from np_x and np_y Atomic Orbitals on Adjacent Atoms.

Metallic Bonding

Metals have several qualities that are unique, such as the ability to conduct electricity, a low ionization energy, and a low electronegativity (so they will give up electrons easily, i.e., they are cations). Metallic bonding is sort of like covalent bonding, because it involves sharing electrons. The simplest model of metallic bonding is the "sea of electrons" model, which imagines that the atoms sit in a sea of valence electrons that are delocalized over all the atoms. Because there are not specific bonds between individual atoms, metals are more flexible. The atoms can move around and the electron sea will keep holding them together. Some metals are very hard and have very high melting points, while others are soft and have low melting points. This depends roughly on the number of valence electrons that form the sea.

A False Dichotomy: The Ionic vs. Colvalent

The covalent-ionic continuum described above is certainly an improvement over the old covalent -versus - ionic dichotomy that existed only in the textbook and classroom, but it is still only a one-dimensional view of a multidimensional world, and thus a view that hides more than it reveals. The main thing missing is any allowance for the type of bonding that occurs between more pairs of elements than any other: metallic bonding. Intermetallic compounds are rarely even mentioned in introductory courses, but since most of the elements are metals, there are a lot of them, and many play an important role in metallurgy. In metallic bonding, the valence electrons lose their association with individual atoms; they form what amounts to a mobile "electron fluid" that fills the space between the crystal lattice positions occupied by the atoms, (now essentially positive ions.) The more readily this electron delocalization occurs, the more "metallic" the element.

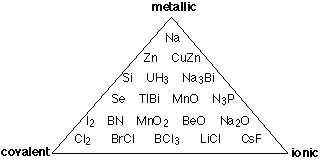
Thus instead of the one-dimension chart shown above, we can construct a triangular diagram whose corners represent the three extremes of "pure" covalent, ionic, and metallic bonding.

Summary

The covalent bond is formed when two atoms are able to share electrons:

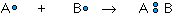
whereas the ionic bond is formed when the "sharing" is so unequal that an electron from atom A is completely lost to atom B, resulting in a pair of ions:

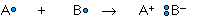
The two extremes of electron sharing represented by the covalent and ionic models appear to be generally consistent with the observed properties of molecular and ionic solids and liquids. But does this mean that there are really two kinds of chemical bonds, ionic and covalent?

Contributors

• Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

• Modified by Tom Neils (Grand Rapids Community College)