2.9 The Nature of Light
- Page ID
- 142184
Skills to Develop
- To learn about the characteristics of electromagnetic waves. Light, X-Rays, infrared and microwaves are among the types of electromagnetic waves.
Scientists discovered much of what we know about the structure of the atom by observing the interaction of atoms with various forms of radiant, or transmitted, energy, such as the energy associated with the visible light we detect with our eyes, the infrared radiation we feel as heat, the ultraviolet light that causes sunburn, and the x-rays that produce images of our teeth or bones. All these forms of radiant energy should be familiar to you. We begin our discussion of the development of our current atomic model by describing the properties of waves and the various forms of electromagnetic radiation.

Properties of Waves
A wave is a periodic oscillation that transmits energy through space. Anyone who has visited a beach or dropped a stone into a puddle has observed waves traveling through water (Figure \(\PageIndex{1}\)). These waves are produced when wind, a stone, or some other disturbance, such as a passing boat, transfers energy to the water, causing the surface to oscillate up and down as the energy travels outward from its point of origin. As a wave passes a particular point on the surface of the water, anything floating there moves up and down.
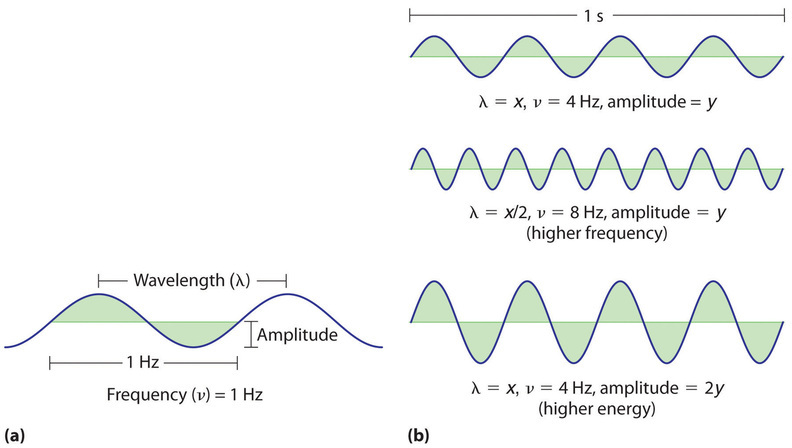
Waves have characteristic properties (Figure \(\PageIndex{2}\)). As you may have noticed in Figure \(\PageIndex{1}\), waves are periodic, that is, they repeat regularly in both space and time. The distance between two corresponding points in a wave—between the midpoints of two peaks, for example, or two troughs—is the wavelength (\(\lambda\), lowercase Greek lambda). Wavelengths are described by a unit of distance, typically meters. The frequency (\(\nu\), lowercase Greek nu) of a wave is the number of oscillations that pass a particular point in a given period of time. The usual units are oscillations per second (1/s = s−1), which in the SI system is called the hertz (Hz). It is named after German physicist Heinrich Hertz (1857–1894), a pioneer in the field of electromagnetic radiation.
The amplitude, or vertical height, of a wave is defined as half the peak-to-trough height; as the amplitude of a wave with a given frequency increases, so does its energy. As you can see in Figure \(\PageIndex{2}\), two waves can have the same amplitude but different wavelengths and vice versa. The distance traveled by a wave per unit time is its speed (\(v\)), which is typically measured in meters per second (m/s). The speed of a wave is equal to the product of its wavelength and frequency:
\[\begin{align} (\text{wavelength})(\text{frequency}) &= \text{speed} onumber \\[4pt] \lambda \nu &=v \label{2.9.1a} \\[4pt] \left ( \dfrac{meters}{\cancel{wave}} \right )\left ( \dfrac{\cancel{\text{wave}}}{\text{second}} \right ) &=\dfrac{\text{meters}}{\text{second}} \label{2.9.1b} \end{align}\]
Be careful not to confuse the symbols for the speed, \(v\), with the frequency, \(\nu\).
Different types of waves may have vastly different possible speeds and frequencies. Water waves are slow compared to sound waves, which can travel through solids, liquids, and gases. Whereas water waves may travel a few meters per second, the speed of sound in dry air at 20°C is 343.5 m/s. Ultrasonic waves, which travel at an even higher speed (>1500 m/s) and have a greater frequency, are used in such diverse applications as locating underwater objects and the medical imaging of internal organs.
Electromagnetic Radiation
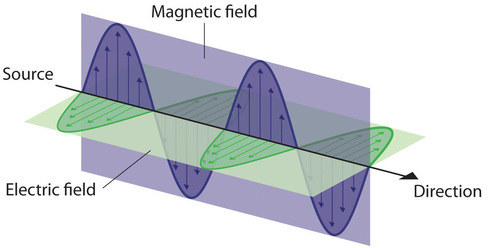
Water waves transmit energy through space by the periodic oscillation of matter (the water). In contrast, energy that is transmitted, or radiated, through space in the form of periodic oscillations of electric and magnetic fields is known as electromagnetic radiation. (Figure \(\PageIndex{3}\)). Some forms of electromagnetic radiation are shown in Figure \(\PageIndex{4}\). In a vacuum, all forms of electromagnetic radiation—whether microwaves, visible light, or gamma rays—travel at the speed of light (c), which turns out to be a fundamental physical constant with a value of 2.99792458 × 108 m/s (about 3.00 ×108 m/s or 1.86 × 105 mi/s). This is about a million times faster than the speed of sound.
Because the various kinds of electromagnetic radiation all have the same speed (c), they differ in only wavelength and frequency. As shown in Figure \(\PageIndex{4}\) and Table \(\PageIndex{1}\), the wavelengths of familiar electromagnetic radiation range from 101 m for radio waves to 10−12 m for gamma rays, which are emitted by nuclear reactions. By replacing \(v\) with \(c\) in Equation\(\ref{2.9.1a}\), we can show that the frequency of electromagnetic radiation is inversely proportional to its wavelength:
\[ \begin{align} c&=\lambda \nu \\[4pt] \nu &=\dfrac{c}{\lambda } \label{2.9.2} \end{align} \]
For example, the frequency of radio waves is about 108 Hz, whereas the frequency of gamma rays is about 1020 Hz. Visible light, which is electromagnetic radiation that can be detected by the human eye, has wavelengths between about 7 × 10−7 m (700 nm, or 4.3 × 1014 Hz) and 4 × 10−7 m (400 nm, or 7.5 × 1014 Hz). Note that when frequency increases, wavelength decreases; c being a constant stays the same. Similarly, when frequency decreases, the wavelength increases.
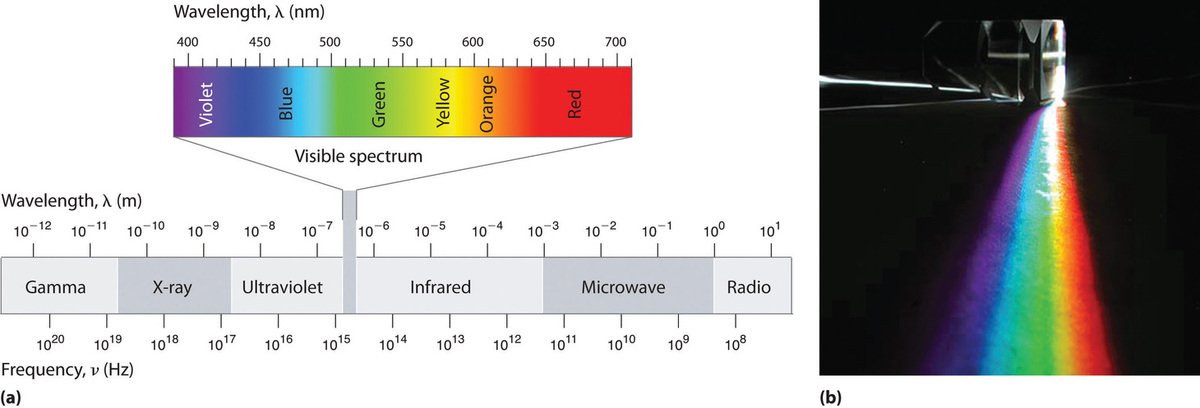
Within the visible range our eyes perceive radiation of different wavelengths (or frequencies) as light of different colors, ranging from red to violet in order of decreasing wavelength. The components of white light—a mixture of all the frequencies of visible light—can be separated by a prism, as shown in part (b) in Figure \(\PageIndex{4}\). A similar phenomenon creates a rainbow, where water droplets suspended in the air act as tiny prisms.
| Unit | Symbol | Wavelength (m) | Type of Radiation |
|---|---|---|---|
| picometer | pm | 10−12 | gamma ray |
| angstrom | Å | 10−10 | x-ray |
| nanometer | nm | 10−9 | UV, visible |
| micrometer | μm | 10−6 | infrared |
| millimeter | mm | 10−3 | infrared |
| centimeter | cm | 10−2 | microwave |
| meter | m | 100 | radio |
As you will soon see, the energy of electromagnetic radiation is directly proportional to its frequency and inversely proportional to its wavelength:
\[ \begin{align} E\; &\propto\; \nu \label{2.9.3} \\[4pt] & \propto\; \dfrac{1}{\lambda } \label{2.9.4} \end{align}\]
Whereas visible light is essentially harmless to our skin, ultraviolet light, with wavelengths of ≤ 400 nm, has enough energy to cause severe damage to our skin in the form of sunburn. Because the ozone layer of the atmosphere absorbs sunlight with wavelengths less than 350 nm, it protects us from the damaging effects of highly energetic ultraviolet radiation.
The energy of electromagnetic radiation increases with increasing frequency and decreasing wavelength.
Example \(\PageIndex{1}\): Wavelength of Radiowaves
Your favorite FM radio station, WXYZ, broadcasts at a frequency of 101.1 MHz. What is the wavelength of this radiation?
Given: frequency
Asked for: wavelength
Strategy:
Substitute the value for the speed of light in meters per second into Equation \(\ref{2.9.2}\) to calculate the wavelength in meters.
Solution:
From Equation \(\ref{2.9.2}\), we know that the product of the wavelength and the frequency is the speed of the wave, which for electromagnetic radiation is 2.998 × 108 m/s:
\[ \begin{align*} \lambda\nu &= c \\[4pt] &= 2.998 \times 10^8 m/s \end{align*} \]
Thus the wavelength \(λ\) is given by
\[ \begin{align*} \lambda &=\dfrac{c}{\nu } \\[4pt] &=\left ( \dfrac{2.988\times 10^{8}\; m/\cancel{s}}{101.1\; \cancel{MHz}} \right )\left ( \dfrac{1\; \cancel{MHz}}{10^{6}\; \cancel{s^{-1}}} \right ) \\[4pt] &=2.965\; m \end{align*} \]
Exercise \(\PageIndex{1}\)
As the police officer was writing up your speeding ticket, she mentioned that she was using a state-of-the-art radar gun operating at 35.5 GHz. What is the wavelength of the radiation emitted by the radar gun?
- Answer
-
8.45 mm
Light is also Particulate!
We have just spent quite a bit of space describing the wave-like properties of electromagnetic radiation. It turns out, however, that several experimental results showed that light did not always act in a wave-like manner, but instead acted as if it consisted of particles. One of these experimental results involved blackbody radiation. The term “blackbody” was coined by Gustav R. Kirchhoff in 1862. The blackbody radiation curve was known experimentally, but its shape eluded physical explanation until the year 1900. The classical approach to the blackbody radiation problem, known as the Rayleigh-Jeans law, in which radiation is treated as waves (as you have learned above), fails to correctly reproduce experimental results. In the limit of short wavelengths, the classical approach predicts infinite radiation intensity, which is inconsistent with the experimental results in which radiation intensity has finite values in the ultraviolet region of the spectrum. This divergence between the results of classical theory and experiments, which came to be called the ultraviolet catastrophe, shows how classical physics fails to explain the mechanism of blackbody radiation, Figure \(\PageIndex{5}\) .

Figure \(\PageIndex{5}\): The ultraviolet catastrophe: The Rayleigh–Jeans law does not explain the observed blackbody emission spectrum.
The blackbody radiation problem was solved in 1900 by Max Planck. The innovative idea that Planck introduced in his model is the assumption that electromagnetic radiation must exist as individual packets of energy, which he called quanta. Planck related the energy of electromagnetic radiation to its frequency by the equation
\[E = h\times \nu \label{2.9.5}\]
In Equation \(\ref{2.9.5}\), \(\nu\) is the frequency of the electromagnetic radiation. The physical constant \(h\) is called Planck’s constant:
\[h = 6.626 \times 10^{-34} J \cdot s \]
Planck’s blackbody radiation law is in agreement with the experimental blackbody radiation curve (Figure \(\PageIndex{6}\)):

Figure \(\PageIndex{6}\): Planck’s theoretical result (continuous curve) and the experimental blackbody radiation curve (dots).
When Planck first published his result, the hypothesis of an energy quantum was not taken seriously by the physics community because it did not follow from any established physics theory at that time. It was perceived, even by Planck himself, as a useful mathematical trick that led to a good theoretical “fit” to the experimental curve. This perception was changed in 1905 when Einstein published his explanation of the photoelectric effect, another experiment that was best explained if electromagnetic radiation was acting as individual particles. In Einstein's explanation of the photoelectric effect, he gave Planck’s energy quantum a new meaning: that of a particle of light. Einstein also gave a new name to Planck's quantum of electromagnetic enegry: a photon.
The concept of the photon had emerged from experimentation with thermal blackbody radiation, electromagnetic radiation emitted as the result of a source’s temperature, which produces a continuous spectrum of energies. However, more direct evidence was needed to verify the quantized nature of energy in all matter. In the next section, we describe how observation of the interaction of individual atoms with visible light provided this evidence.
Line Spectra
Although objects at high temperature emit a continuous spectrum of electromagnetic radiation, a different kind of spectrum is observed when pure samples of individual elements are heated. For example, when a high-voltage electrical discharge is passed through a sample of hydrogen gas at low pressure, the resulting individual isolated hydrogen atoms caused by the dissociation of H2 emit a red light. Unlike blackbody radiation, the color of the light emitted by the hydrogen atoms does not depend greatly on the temperature of the gas in the tube. When the emitted light is passed through a prism, only a few narrow lines of particular wavelengths, called a line spectrum, are observed rather than a continuous range of wavelengths (Figure \(\PageIndex{6}\)). The light emitted by hydrogen atoms is red because, of its four characteristic lines, the most intense line in its spectrum is in the red portion of the visible spectrum, at 656 nm. With sodium, however, we observe a yellow color because the most intense lines in its spectrum are in the yellow portion of the spectrum, at about 589 nm.


Figure \(\PageIndex{6}\): The Emission of Light by Hydrogen Atoms. (a) A sample of excited hydrogen atoms emits a characteristic red light. (b) When the light emitted by a sample of excited hydrogen atoms is split into its component wavelengths by a prism, four characteristic violet, blue, green, and red emission lines can be observed, the most intense of which is at 656 nm.
Such emission spectra were observed for many other elements in the late 19th century, which presented a major challenge because classical physics was unable to explain them. Part of the explanation is provided by Planck’s equation: the observation of only a few values of λ (or \(\nu \)) in the line spectrum meant that only a few values of E were possible. Thus the energy levels of a hydrogen atom had to be quantized; in other words, only states that had certain values of energy were possible, or allowed. If a hydrogen atom could have any value of energy, then a continuous spectrum would have been observed, similar to blackbody radiation.
Bohr's Model
In 1913, a Danish physicist, Niels Bohr (1885–1962; Nobel Prize in Physics, 1922), proposed a theoretical model for the hydrogen atom that explained its emission spectrum. Bohr’s model required only one assumption: The electron moves around the nucleus in circular orbits that can have only certain allowed radii. Rutherford’s earlier model of the atom had also assumed that electrons moved in circular orbits around the nucleus and that the atom was held together by the electrostatic attraction between the positively charged nucleus and the negatively charged electron. Although we now know that the assumption of circular orbits was incorrect, Bohr’s insight was to propose that the electron could occupy only certain regions of space.
Bohr’s model of the hydrogen atom gave an exact explanation for its observed emission spectrum. The following are his key contributions to our understanding of atomic structure:
- Electrons can occupy only certain regions of space, called orbits.
- Orbits closer to the nucleus are lower in energy.
- Electrons can move from one orbit to another by absorbing or emitting energy, giving rise to characteristic spectra.
Unfortunately, Bohr could not explain why the electron should be restricted to particular orbits. Also, despite a great deal of tinkering, such as assuming that orbits could be ellipses rather than circles, his model could not quantitatively explain the emission spectra of any element other than hydrogen (Figure \(\PageIndex{7}\)). In fact, Bohr’s model worked only for species that contained just one electron: H, He+, Li2+, and so forth. Scientists needed a fundamental change in their way of thinking about the electronic structure of atoms to advance beyond the Bohr model.



Figure \(\PageIndex{7}\): The Emission Spectra of Elements Compared with Hydrogen. These images show (a) hydrogen gas, which is atomized to hydrogen atoms in the discharge tube; (b) neon; and (c) mercury. The strongest lines in the hydrogen spectrum are in the far UV Lyman series starting at 124 nm and below. The strongest lines in the mercury spectrum are at 181 and 254 nm, also in the UV. These are not shown.
Summary
Understanding the electronic structure of atoms requires an understanding of the properties of waves and electromagnetic radiation. A wave is a periodic oscillation by which energy is transmitted through space. All waves are periodic, repeating regularly in both space and time. Waves are characterized by several interrelated properties: wavelength (\(λ\)), the distance between successive waves; frequency (\( u\)), the number of waves that pass a fixed point per unit time; speed (\(v\)), the rate at which the wave propagates through space; and amplitude, the magnitude of the oscillation about the mean position. The speed of a wave is equal to the product of its wavelength and frequency. Electromagnetic radiation consists of two perpendicular waves, one electric and one magnetic, propagating at the speed of light (\(c\)). Electromagnetic radiation is radiant energy that includes radio waves, microwaves, visible light, x-rays, and gamma rays, which differ in their frequencies and wavelengths.
There is an intimate connection between the atomic structure of an atom and its spectral characteristics. Atoms of individual elements emit light at only specific wavelengths, producing a line spectrum rather than the continuous spectrum of all wavelengths produced by a hot object. Niels Bohr explained the line spectrum of the hydrogen atom by assuming that the electron moved in circular orbits and that orbits with only certain radii were allowed. Lines in the spectrum were due to transitions in which an electron moved from a higher-energy orbit with a larger radius to a lower-energy orbit with smaller radius. The orbit closest to the nucleus represented the ground state of the atom and was most stable; orbits farther away were higher-energy excited states. Transitions from an excited state to a lower-energy state resulted in the emission of light with only a limited number of wavelengths. Atoms can also absorb light of certain energies, resulting in a transition from the ground state or a lower-energy excited state to a higher-energy excited state. This produces an absorption spectrum, which has dark lines in the same position as the bright lines in the emission spectrum of an element. Bohr’s model revolutionized the understanding of the atom but could not explain the spectra of atoms heavier than hydrogen.
Contributors
Modified by Joshua Halpern (Howard University)
- Modified by Tom Neils (Grand Rapids Community College)

