7.4 Changes in Heat that Acompany Reactions
- Page ID
- 220937
When we study energy changes in chemical reactions, we call the change in heat the change in enthalpy of reaction (\(ΔH_{rxn}\)). If heat flows from a system to its surroundings, the enthalpy of the system decreases, so \(ΔH_{rxn}\) is negative. (Energy is like money:if you lose or spend money, then you subtract that money from your account. Likewise if a reaction loses heat, then you subtract the heat.) Conversely, if heat flows from the surroundings into a system, the enthalpy of the system increases, so \(ΔH_{rxn}\) is positive. Thus:
- \(ΔH_{rxn} < 0\) for an exothermic reaction, and
- \(ΔH_{rxn} > 0\) for an endothermic reaction.
Bond breaking always requires an input of energy and is therefore an endothermic process, whereas bond making always releases energy, which is an exothermic process. The sign conventions for heat flow and enthalpy changes are summarized in the following table:
| Reaction Type | ΔHrxn |
|---|---|
| exothermic | < 0 (heat flows from a system to its surroundings) |
| endothermic | > 0 (heat flows from the surroundings to a system) |
If ΔHrxn is negative, then the enthalpy of the products is less than the enthalpy of the reactants; that is, an exothermic reaction is energetically downhill (Figure \(\PageIndex{2}a\)). Conversely, if ΔHrxn is positive, then the enthalpy of the products is greater than the enthalpy of the reactants; thus, an endothermic reaction is energetically uphill (Figure \(\PageIndex{2b}\)). Two important characteristics of enthalpy and changes in enthalpy are summarized in the following discussion.
Bond breaking ALWAYS requires an input of energy; bond making ALWAYS releases energy.
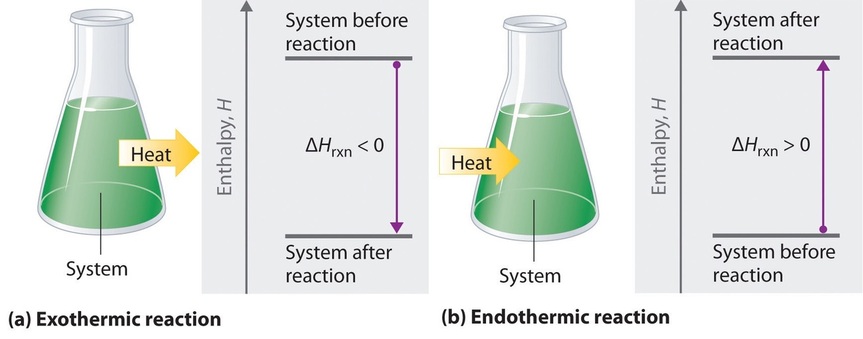
Figure \(\PageIndex{2}\): The Enthalpy of Reaction. Energy changes in chemical reactions are usually measured as changes in enthalpy. (a) If heat flows from a system to its surroundings, the enthalpy of the system decreases, ΔHrxn is negative, and the reaction is exothermic; it is energetically downhill. (b) Conversely, if heat flows from the surroundings to a system, the enthalpy of the system increases, ΔHrxn is positive, and the reaction is endothermic; it is energetically uphill.
-
Reversing a reaction or a process changes the sign of ΔH. Ice absorbs heat when it melts (IMFs are broken), so liquid water must release heat when it freezes (IMFs are formed):
\( \begin{matrix}
heat+ H_{2}O(s) \rightarrow H_{2}O(l) & \Delta H > 0
\end{matrix} \label{5.4.7} \)\( \begin{matrix}
H_{2}O(l) \rightarrow H_{2}O(s) + heat & \Delta H < 0
\end{matrix} \label{5.4.8} \)In both cases, the magnitude of the enthalpy change is the same; only the sign is different.
-
Enthalpy is an extensive property (like mass). The magnitude of ΔH for a reaction is proportional to the amounts of the substances that react. For example, a large fire produces more heat than a single match, even though the chemical reaction—the combustion of wood—is the same in both cases. For this reason, the enthalpy change for a reaction is usually given in kilojoules per mole of a particular reactant or product. Consider Equation \(\ref{5.4.9}\), which describes the reaction of aluminum with iron(III) oxide (Fe2O3) at constant pressure. According to the reaction stoichiometry, 2 mol of Fe, 1 mol of Al2O3, and 851.5 kJ of heat are produced for every 2 mol of Al and 1 mol of Fe2O3 consumed:
\[ 2Al\left (s \right )+Fe_{2}O_{3}\left (s \right ) \rightarrow 2Fe\left (s \right )+Al_{2}O_{3}\left (s \right )+ 815.5 \; kJ \label{5.4.9} \]
Thus ΔH = −851.5 kJ/mol of Fe2O3. We can also describe ΔH for the reaction as −425.8 kJ/mol of Al: because 2 mol of Al are consumed in the balanced chemical equation, we divide −851.5 kJ by 2. When a value for ΔH, in kilojoules rather than kilojoules per mole, is written after the reaction, as in Equation \(\ref{5.4.10}\), it is the value of ΔH corresponding to the reaction of the molar quantities of reactants as given in the balanced chemical equation:
\[ 2Al\left (s \right )+Fe_{2}O_{3}\left (s \right ) \rightarrow 2Fe\left (s \right )+Al_{2}O_{3}\left (s \right ) \;\;\;\; \Delta H_{rxn}= - 851.5 \; kJ \label{5.4.10} \]
If 4 mol of Al and 2 mol of Fe2O3 react, the change in enthalpy is 2 × (−851.5 kJ) = −1703 kJ. We can summarize the relationship between the amount of each substance and the enthalpy change for this reaction as follows:
\[ - \dfrac{851.5 \; kJ}{2 \; mol \;Al} = - \dfrac{425.8 \; kJ}{1 \; mol \;Al} = - \dfrac{1703 \; kJ}{4 \; mol \; Al} \label{5.4.6a} \]
The relationship between the magnitude of the enthalpy change and the mass of reactants is illustrated in Example \(\PageIndex{1}\).
Example \(\PageIndex{1}\): Melting Icebergs
Certain parts of the world, such as southern California and Saudi Arabia, are short of freshwater for drinking. One possible solution to the problem is to tow icebergs from Antarctica and then melt them as needed. If \(ΔH\) is 6.01 kJ/mol for the reaction at 0°C and constant pressure:
\[\ce{H2O(s) → H_2O(l)} \nonumber\]
How much energy would be required to melt a moderately large iceberg with a mass of 1.00 million metric tons (1.00 × 106 metric tons)? (A metric ton is 1000 kg.)
Given: energy per mole of ice and mass of iceberg
Asked for: energy required to melt iceberg
Strategy:
- Calculate the number of moles of ice contained in 1 million metric tons (1.00 × 106 metric tons) of ice.
- Calculate the energy needed to melt the ice by multiplying the number of moles of ice in the iceberg by the amount of energy required to melt 1 mol of ice.
Solution:
A Because enthalpy is an extensive property, the amount of energy required to melt ice depends on the amount of ice present. We are given ΔH for the process—that is, the amount of energy needed to melt 1 mol (or 18.015 g) of ice—so we need to calculate the number of moles of ice in the iceberg and multiply that number by ΔH (+6.01 kJ/mol):
\[ \begin{align*} moles \; H_{2}O & = 1.00\times 10^{6} \; \cancel{\text{metric ton }} \ce{H2O} \left ( \dfrac{1000 \; \cancel{kg}}{1 \; \cancel{\text{metric ton}}} \right ) \left ( \dfrac{1000 \; \cancel{g}}{1 \; \cancel{kg}} \right ) \left ( \dfrac{1 \; mol \; H_{2}O}{18.015 \; \cancel{g \; H_{2}O}} \right ) \\[5pt] & = 5.55\times 10^{10} \; mol \,\ce{H2O} \end{align*} \]
B The energy needed to melt the iceberg is thus
\[ \left ( \dfrac{6.01 \; kJ}{\cancel{mol \; H_{2}O}} \right )\left ( 5.55 \times 10^{10} \; \cancel{mol \; H_{2}O} \right )= 3.34 \times 10^{11} \; kJ \nonumber \]
Because so much energy is needed to melt the iceberg, this plan would require a relatively inexpensive source of energy to be practical. To give you some idea of the scale of such an operation, the amounts of different energy sources equivalent to the amount of energy needed to melt the iceberg are shown below.
Possible sources of the approximately \(3.34 \times 10^{11}\, kJ\) needed to melt a \(1.00 \times 10^6\) metric ton iceberg
- Combustion of 3.8 × 103 ft3 of natural gas
- Combustion of 68,000 barrels of oil
- Combustion of 15,000 tons of coal
- \(1.1 \times 10^8\) kilowatt-hours of electricity
Alternatively, we can rely on ambient temperatures to slowly melt the iceberg. The main issue with this idea is the cost of dragging the iceberg to the desired place.
Exercise \(\PageIndex{1}\): Thermite Reaction
If 17.3 g of powdered aluminum are allowed to react with excess \(\ce{Fe2O3}\), how much heat is produced?
- Answer
-
273 kJ
The sign convention is the same for all enthalpy changes: negative if heat is released by the system and positive if heat is absorbed by the system.
Summary
For a chemical reaction, the enthalpy of reaction (\(ΔH_{rxn}\)) is the difference in enthalpy between products and reactants; the units of \(ΔH_{rxn}\) are kilojoules per mole. Reversing a chemical reaction reverses the sign of \(ΔH_{rxn}\).
Contributors
Modified by Joshua Halpern (Howard University)
- Modified by Tom Neils (Grand Rapids Community College)

