3.5 What about the Electrons? Part 2: Quantum Mechanics
- Page ID
- 218240
Skills to Develop
- To apply the results of quantum mechanics to chemistry.
The wavelike nature of subatomic particles such as the electron made it impossible to use the equations of classical physics to describe the motion of electrons in atoms. Scientists needed a new approach that took the wave behavior of the electron into account. In 1926, an Austrian physicist, Erwin Schrödinger (1887–1961; Nobel Prize in Physics, 1933), developed wave mechanics, a mathematical technique that describes the relationship between the motion of a particle that exhibits wavelike properties (such as an electron) and its allowed energies.
Erwin Schrödinger (1887–1961)
Schrödinger’s unconventional approach to atomic theory was typical of his unconventional approach to life. He was notorious for his intense dislike of memorizing data and learning from books. When Hitler came to power in Germany, Schrödinger escaped to Italy. He then worked at Princeton University in the United States but eventually moved to the Institute for Advanced Studies in Dublin, Ireland, where he remained until his retirement in 1955.
Although quantum mechanics uses sophisticated mathematics, you do not need to understand the mathematical details to follow our discussion of its general conclusions. We focus on the properties of the wavefunctions that are the solutions of Schrödinger’s equations.
Wavefunctions
A wavefunction (Ψ) is a mathematical function that relates the location of an electron at a given point in space (identified by x, y, and z coordinates) to the amplitude of its wave, which corresponds to its energy. Thus each wavefunction is associated with a particular energy E. The properties of wavefunctions derived from quantum mechanics are summarized here:
- A wavefunction uses three variables to describe the position of an electron. A fourth variable is usually required to fully describe the location of objects in motion. Three specify the position in space (as with the Cartesian coordinates x, y, and z), and one specifies the time at which the object is at the specified location. For example, if you were the captain of a ship trying to intercept an enemy submarine, you would need to know its latitude, longitude, and depth, as well as the time at which it was going to be at this position (Figure 6.5.1). For electrons, we can ignore the time dependence because we will be using standing waves, which by definition do not change with time, to describe the position of an electron.
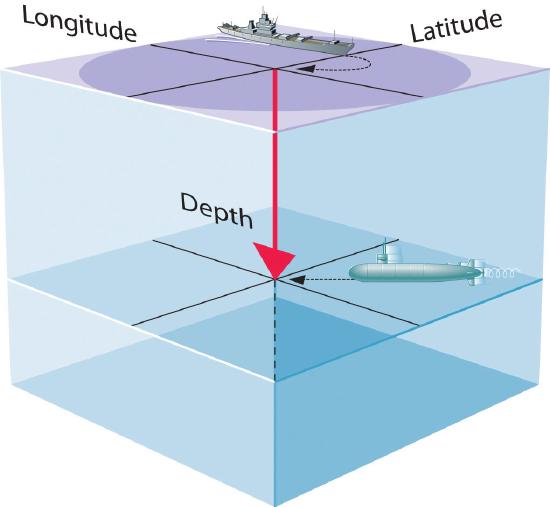
Figure \(\PageIndex{1}\): The Four Variables (Latitude, Longitude, Depth, and Time) required to precisely locate an object
- The square of the wavefunction at a given point is proportional to the probability of finding an electron at that point, which leads to a distribution of probabilities in space. The square of the wavefunction (\(\Psi^2\)) is proportional to the probability of finding an electron at a given point. We use probabilities because, according to Heisenberg’s uncertainty principle, we cannot precisely specify the position of an electron. The probability of finding an electron at any point in space depends on several factors, including the distance from the nucleus and, in many cases, the atomic equivalent of latitude and longitude. As one way of graphically representing the probability distribution, the probability of finding an electron is indicated by the density of colored dots, as shown for the ground state of the hydrogen atom in Figure \(\PageIndex{2}\).
- Each wavefunction is associated with a particular energy. As in Bohr’s model, the energy of an electron in an atom is quantized; it can have only certain allowed values. The major difference between Bohr’s model and Schrödinger’s approach is that Bohr had to impose the idea of quantization arbitrarily, whereas in Schrödinger’s approach, quantization is a natural consequence of describing an electron as a standing wave.
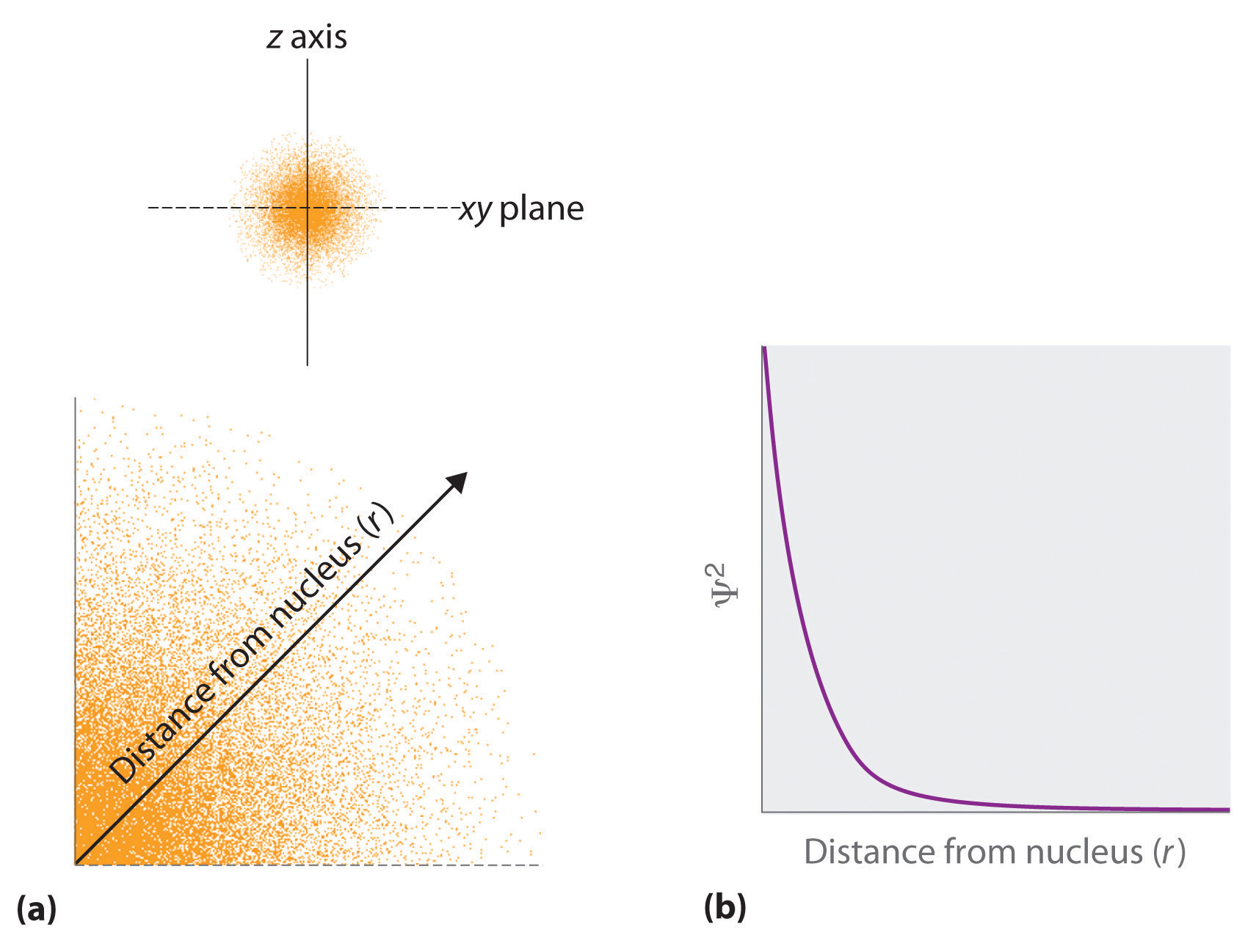
Figure \(\PageIndex{2}\): Probability of Finding the Electron in the Ground State of the Hydrogen Atom at Different Points in Space. (a) The density of the dots shows electron probability. (b) In this plot of Ψ2 versus r for the ground state of the hydrogen atom, the electron probability density is greatest at r = 0 (the nucleus) and falls off with increasing r. Because the line never actually reaches the horizontal axis, the probability of finding the electron at very large values of r is very small but not zero.
An orbital is the quantum mechanical refinement of Bohr’s orbit. In contrast to his concept of a simple circular orbit with a fixed radius, orbitals are mathematically derived regions of space with different probabilities of containing an electron.
Summary
There is a relationship between the locations of electrons in atoms and molecules and their energies that is described by quantum mechanics. Because of wave–particle duality, scientists must deal with the probability of an electron being at a particular point in space. To do so required the development of quantum mechanics, which uses wavefunctions (Ψ) to describe the mathematical relationship between the location of electrons in atoms and molecules and their energies. Wavefunctions have four important properties:
- the wavefunction uses three variables (Cartesian axes x, y, and z) to describe the position of an electron;
- the probability of finding an electron at a given point is proportional to the square of the wavefunction at that point, leading to a distribution of probabilities in space that is often portrayed as an electron density plot;
- describing electron distributions as standing waves leads naturally to the existence of sets of quantum numbers characteristic of each wavefunction; and
- each spatial distribution of the electron described by a wavefunction with a given set of quantum numbers has a particular energy.
- Each wavefunction with a given set of quantum numbers describes a particular spatial distribution of an electron in an atom, an atomic orbital.
- Because its average distance from the nucleus determines the energy of an electron, each atomic orbital with a given set of quantum numbers has a particular energy associated with it, the orbital energy.
- An atom or ion with the electron(s) in the lowest-energy orbital(s) is said to be in its ground state, whereas an atom or ion in which one or more electrons occupy higher-energy orbitals is said to be in an excited state.
- When an atom absorbs the correct amount of energy, an electron will be promoted to a higher energy orbital. This process is called atomic absorption, and it creates an excited-state atom.
- When an excited-state atom "relaxes", an electron in a higher energy orbital than it would normally occupy gives off energy as it returns to a lower energy orbital (not always to the ground state!). This process is called atomic emission, and it is generally accompanied by the emission of visible light.
Contributors
Modified by Joshua Halpern (Howard University)
- Modified by Tom Neils (Grand Rapids Community College)

