2.1.8: Strength of Covalent Bonds
- Last updated
- Save as PDF
- Page ID
- 287934
Learning Objectives
- The define Bond-dissociation energy (bond energy)
- To correlate bond strength with bond length
- To define and used average bond energies
In proposing his theory that octets can be completed by two atoms sharing electron pairs, Lewis provided scientists with the first description of covalent bonding. In this section, we expand on this and describe some of the properties of covalent bonds. The stability of a molecule is a function of the strength of the covalent bonds holding the atoms together.
The Relationship between Bond Order and Bond Energy
Triple bonds between like atoms are shorter than double bonds, and because more energy is required to completely break all three bonds than to completely break two, a triple bond is also stronger than a double bond. Similarly, double bonds between like atoms are stronger and shorter than single bonds. Bonds of the same order between different atoms show a wide range of bond energies, however. Table \(\PageIndex{1}\) lists the average values for some commonly encountered bonds. Although the values shown vary widely, we can observe four trends:
| Single Bonds | Multiple Bonds | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H–H | 432 | C–C | 346 | N–N | ≈167 | O–O | ≈142 | F–F | 155 | C=C | 602 |
| H–C | 411 | C–Si | 318 | N–O | 201 | O–F | 190 | F–Cl | 249 | C≡C | 835 |
| H–Si | 318 | C–N | 305 | N–F | 283 | O–Cl | 218 | F–Br | 249 | C=N | 615 |
| H–N | 386 | C–O | 358 | N–Cl | 313 | O–Br | 201 | F–I | 278 | C≡N | 887 |
| H–P | ≈322 | C–S | 272 | N–Br | 243 | O–I | 201 | Cl–Cl | 240 | C=O | 749 |
| H–O | 459 | C–F | 485 | P–P | 201 | S–S | 226 | Cl–Br | 216 | C≡O | 1072 |
| H–S | 363 | C–Cl | 327 | S–F | 284 | Cl–I | 208 | N=N | 418 | ||
| H–F | 565 | C–Br | 285 | S–Cl | 255 | Br–Br | 190 | N≡N | 942 | ||
| H–Cl | 428 | C–I | 213 | S–Br | 218 | Br–I | 175 | N=O | 607 | ||
| H–Br | 362 | Si–Si | 222 | I–I | 149 | O=O | 494 | ||||
| H–I | 295 | Si–O | 452 | S=O | 532 | ||||||
| Source: Data from J. E. Huheey, E. A. Keiter, and R. L. Keiter, Inorganic Chemistry, 4th ed. (1993). | |||||||||||
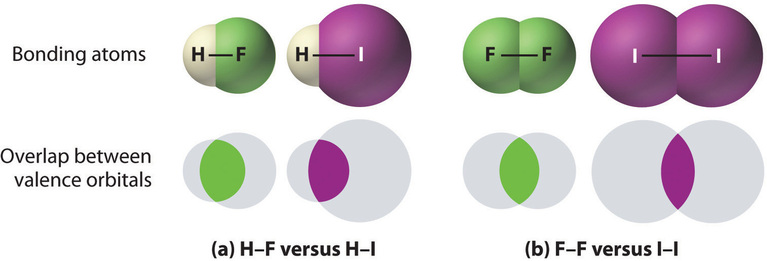
- Bonds between hydrogen and atoms in the same column of the periodic table decrease in strength as we go down the column. Thus an H–F bond is stronger than an H–I bond, H–C is stronger than H–Si, H–N is stronger than H–P, H–O is stronger than H–S, and so forth. The reason for this is that the region of space in which electrons are shared between two atoms becomes proportionally smaller as one of the atoms becomes larger (part (a) in Figure 8.11).
- Bonds between like atoms usually become weaker as we go down a column (important exceptions are noted later). For example, the C–C single bond is stronger than the Si–Si single bond, which is stronger than the Ge–Ge bond, and so forth. As two bonded atoms become larger, the region between them occupied by bonding electrons becomes proportionally smaller, as illustrated in part (b) in Figure 8.11. Noteworthy exceptions are single bonds between the period 2 atoms of groups 15, 16, and 17 (i.e., N, O, F), which are unusually weak compared with single bonds between their larger congeners. It is likely that the N–N, O–O, and F–F single bonds are weaker than might be expected due to strong repulsive interactions between lone pairs of electrons on adjacent atoms. The trend in bond energies for the halogens is therefore \[\ce{Cl–Cl > Br–Br > F–F > I–I} \nonumber \] Similar effects are also seen for the O–O versus S–S and for N–N versus P–P single bonds.
Bonds between hydrogen and atoms in a given column in the periodic table are weaker down the column; bonds between like atoms usually become weaker down a column.
- Because elements in periods 3 and 4 rarely form multiple bonds with themselves, their multiple bond energies are not accurately known. Nonetheless, they are presumed to be significantly weaker than multiple bonds between lighter atoms of the same families. Compounds containing an Si=Si double bond, for example, have only recently been prepared, whereas compounds containing C=C double bonds are one of the best-studied and most important classes of organic compounds.
- Multiple bonds between carbon, oxygen, or nitrogen and a period 3 element such as phosphorus or sulfur tend to be unusually strong. In fact, multiple bonds of this type dominate the chemistry of the period 3 elements of groups 15 and 16. Multiple bonds to phosphorus or sulfur occur as a result of d-orbital interactions, as we discussed for the SO42− ion in Section 8.6. In contrast, silicon in group 14 has little tendency to form discrete silicon–oxygen double bonds. Consequently, SiO2 has a three-dimensional network structure in which each silicon atom forms four Si–O single bonds, which makes the physical and chemical properties of SiO2 very different from those of CO2.
Bond strengths increase as bond order increases, while bond distances decrease.
The Relationship between Molecular Structure and Bond Energy
Bond energy is defined as the energy required to break a particular bond in a molecule in the gas phase. Its value depends on not only the identity of the bonded atoms but also their environment. Thus the bond energy of a C–H single bond is not the same in all organic compounds. For example, the energy required to break a C–H bond in methane varies by as much as 25% depending on how many other bonds in the molecule have already been broken (Table \(\PageIndex{2}\)); that is, the C–H bond energy depends on its molecular environment. Except for diatomic molecules, the bond energies listed in Table \(\PageIndex{1}\) are average values for all bonds of a given type in a range of molecules. Even so, they are not likely to differ from the actual value of a given bond by more than about 10%.
| Reaction | D (kJ/mol) |
|---|---|
| CH4(g) → CH3(g) + H(g) | 439 |
| CH3(g) → CH2(g) + H(g) | 462 |
| CH2(g) → CH(g) + H(g) | 424 |
| CH(g) → C(g) + H(g) | 338 |
We can estimate the enthalpy change for a chemical reaction by adding together the average energies of the bonds broken in the reactants and the average energies of the bonds formed in the products and then calculating the difference between the two. If the bonds formed in the products are stronger than those broken in the reactants, then energy will be released in the reaction (\(ΔH_{rxn} < 0\)):
\[ ΔH_{rxn} \approx \sum{\text{(bond energies of bonds broken)}}−\sum{\text{(bond energies of bonds formed)}} \label{\(\PageIndex{1}\)} \]
The ≈ sign is used because we are adding together average bond energies; hence this approach does not give exact values for ΔHrxn.
Let’s consider the reaction of 1 mol of n-heptane (C7H16) with oxygen gas to give carbon dioxide and water. This is one reaction that occurs during the combustion of gasoline:
\[\ce{CH3(CH2)5CH3(l) + 11 O2(g) \rightarrow 7 CO2(g) + 8 H2O(g)} \label{\(\PageIndex{2}\)} \]
In this reaction, 6 C–C bonds, 16 C–H bonds, and 11 O=O bonds are broken per mole of n-heptane, while 14 C=O bonds (two for each CO2) and 16 O–H bonds (two for each H2O) are formed. The energy changes can be tabulated as follows:
| Bonds Broken (kJ/mol) | Bonds Formed (kJ/mol) | ||
|---|---|---|---|
| 6 C–C | 346 × 6 = 2076 | 14 C=O | 799 × 14 = 11,186 |
| 16 C–H | 411 × 16 = 6576 | 16 O–H | 459 × 16 = 7344 |
| 11 O=O | 494 × 11 = 5434 | Total = 18,530 | |
| Total = 14,086 | |||
The bonds in the products are stronger than the bonds in the reactants by about 4444 kJ/mol. This means that \(ΔH_{rxn}\) is approximately −4444 kJ/mol, and the reaction is highly exothermic (which is not too surprising for a combustion reaction).
If we compare this approximation with the value obtained from measured \(ΔH_f^o\) values (\(ΔH_{rxn} = −481\;7 kJ/mol\)), we find a discrepancy of only about 8%, less than the 10% typically encountered. Chemists find this method useful for calculating approximate enthalpies of reaction for molecules whose actual \(ΔH^ο_f\) values are unknown. These approximations can be important for predicting whether a reaction is exothermic or endothermic—and to what degree.
Example \(\PageIndex{1}\): Explosives
The compound RDX (Research Development Explosive) is a more powerful explosive than dynamite and is used by the military. When detonated, it produces gaseous products and heat according to the following reaction. Use the approximate bond energies in Table \(\PageIndex{1}\) to estimate the \(ΔH_{rxn}\) per mole of RDX.

Given: chemical reaction, structure of reactant, and Table \(\PageIndex{1}\).
Asked for: \(ΔH_{rxn}\) per mole
Strategy:
- List the types of bonds broken in RDX, along with the bond energy required to break each type. Multiply the number of each type by the energy required to break one bond of that type and then add together the energies. Repeat this procedure for the bonds formed in the reaction.
- Use Equation \(\PageIndex{1}\) to calculate the amount of energy consumed or released in the reaction (ΔHrxn).
Solution:
We must add together the energies of the bonds in the reactants and compare that quantity with the sum of the energies of the bonds in the products. A nitro group (–NO2) can be viewed as having one N–O single bond and one N=O double bond, as follows:
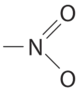
In fact, however, both N–O distances are usually the same because of the presence of two equivalent resonance structures.
A We can organize our data by constructing a table:
| Bonds Broken (kJ/mol) | Bonds Broken (kJ/mol) | ||
|---|---|---|---|
| 6 C–H | 411 × 6 = 2466 | 6 C=O | 799 × 6 = 4794 |
| 3 N–N | 167 × 3 = 501 | 6 O–H | 459 × 6 = 2754 |
| 3 N–O | 201 × 3 = 603 | Total = 10,374 | |
| 3 N=O | 607 × 3 = 1821 | ||
| 1.5 O=O | 494 × 1.5 = 741 | ||
| Total = 7962 | |||
B From Equation \(\PageIndex{1}\), we have
\[ \begin{align*} ΔH_{rxn} &\approx \sum{\text{(bond energies of bonds broken)}}−\sum{\text{(bond energies of bonds formed)}} \\[4pt] &= 7962 \; kJ/mol − 10,374 \; kJ/mol \\[4pt] &=−2412 \;kJ/mol \end{align*} \nonumber \]
Thus this reaction is also highly exothermic
Exercise \(\PageIndex{1}\): Freon
The molecule HCFC-142b is a hydrochlorofluorocarbon that is used in place of chlorofluorocarbons (CFCs) such as the Freons and can be prepared by adding HCl to 1,1-difluoroethylene:
Use tabulated bond energies to calculate \(ΔH_{rxn}\).
- Answer
-
−54 kJ/mol

Bond Dissociation Energy
Bond Dissociation Energy (also referred to as Bond energy) is the enthalpy change (\(\Delta H\), heat input) required to break a bond (in 1 mole of a gaseous substance)
What about when we have a compound which is not a diatomic molecule? Consider the dissociation of methane:
There are four equivalent C-H bonds, thus we can that the dissociation energy for a single C-H bond would be:
\[ \begin{align*} D(C-H) &= (1660/4)\, kJ/mol \\[4pt] &= 415 \,kJ/mol \end{align*} \nonumber \]
The bond energy for a given bond is influenced by the rest of the molecule. However, this is a relatively small effect (suggesting that bonding electrons are localized between the bonding atoms). Thus, the bond energy for most bonds varies little from the average bonding energy for that type of bond
Bond energy is always a positive value - it takes energy to break a covalent bond (conversely energy is released during bond formation)
| Bond | (kJ/mol) |
|---|---|
| C-F | 485 |
| C-Cl | 328 |
| C-Br | 276 |
| C-I | 240 |
| C-C | 348 |
| C-N | 293 |
| C-O | 358 |
| C-F | 485 |
| C-C | 348 |
| C=C | 614 |
| C=C | 839 |
The more stable a molecule (i.e. the stronger the bonds) the less likely the molecule is to undergo a chemical reaction.
Bond Energies and the Enthalpy of Reactions
If we know which bonds are broken and which bonds are made during a chemical reaction, we can estimate the enthalpy change of the reaction (\(\Delta H_{rxn}\)) even if we do not know the enthalpies of formation ((\(\Delta H_{f}^o\))for the reactants and products:
\[\Delta H = \sum \text{bond energies of broken bonds} - \sum \text{bond energies of formed bonds} \label{8.8.3} \]
Example \(\PageIndex{2}\): Chlorination of Methane
What is the enthalpy of reaction between 1 mol of chlorine and 1 mol methane?

Solution
We use Equation \ref{8.8.3}, which requires tabulating bonds broken and formed.
- Bonds broken: 1 mol of Cl-Cl bonds, 1 mol of C-H bonds
- Bonds formed: 1 mol of H-Cl bonds, 1 mol of C-Cl bonds
\[\begin{align*} \Delta H &= [D(Cl-Cl) + D(C-H)] - [D(H-Cl)+D(C-Cl)] \\[4pt] &= [242 kJ + 413 kJ] - [431 kJ + 328 kJ] \\[4pt] &= -104 \,kJ \end{align*} \nonumber \]
Thus, the reaction is exothermic (because the bonds in the products are stronger than the bonds in the reactants)
Example \(\PageIndex{3}\): Combustion of Ethane
What is the enthalpy of reaction for the combustion of 1 mol of ethane?

Solution
We use Equation \ref{8.8.3}, which requires tabulating bonds broken and formed.
- bonds broken: 6 moles C-H bonds, 1 mol C-C bonds, 7/2 moles of O=O bonds
- bonds formed: 4 moles C=O bonds, 6 moles O-H bonds
\[\begin{align*} \Delta {H} &= [(6 \times 413) + (348) + (\frac{7}{2} \times 495)] - [(4 \times 799) + (6 \times 463)] \\[4pt] &= 4558 - 5974 \\[4pt] &= -1416\; kJ \end{align*} \nonumber \]
Therefor the reaction is exothermic.
| Bond | Bond Energy (kJ/mol) | Bond Length (Å) |
|---|---|---|
| C-C | 348 | 1.54 |
| C=C | 614 | 1.34 |
| C=C | 839 | 1. |
As the number of bonds between two atoms increases, the bond grows shorter and stronger
Summary
Bond order is the number of electron pairs that hold two atoms together. Single bonds have a bond order of one, and multiple bonds with bond orders of two (a double bond) and three (a triple bond) are quite common. In closely related compounds with bonds between the same kinds of atoms, the bond with the highest bond order is both the shortest and the strongest. In bonds with the same bond order between different atoms, trends are observed that, with few exceptions, result in the strongest single bonds being formed between the smallest atoms. Tabulated values of average bond energies can be used to calculate the enthalpy change of many chemical reactions. If the bonds in the products are stronger than those in the reactants, the reaction is exothermic and vice versa.
The breakage and formation of bonds is similar to a relationship: you can either get married or divorced and it is more favorable to be married.
- Energy is always released to make bonds, which is why the enthalpy change for breaking bonds is always positive.
- Energy is always required to break bonds. Atoms are much happier when they are "married" and release energy because it is easier and more stable to be in a relationship (e.g., to generate octet electronic configurations). The enthalpy change is always negative because the system is releasing energy when forming bond.

