8.E: Solids, Liquids, and Gases (Exercises)
- Page ID
- 218347
8.1: Intermolecular Interactions
Concept Review Exercise
1. What types of intermolecular interactions can exist in compounds?
2. What is the difference between covalent network and covalent molecular compounds?
Answer
1. ionic bonding, network covalent, dispersion forces, dipole-dipole interactions, and hydrogen bonding.
2. Covalent network compounds contain atoms that are covalently bonded to other individual atoms in a giant 3-dimensional network. Covalent molecular compounds contain individual molecules that are attracted to one another through dispersion, dipole-dipole or hydrogen bonding.
Exercises
-
List the three common phases in the order you are likely to find them—from lowest temperature to highest temperature.
-
List the three common phases in the order they exist from lowest energy to highest energy.
-
List these intermolecular interactions from weakest to strongest: London forces, hydrogen bonding, and ionic interactions.
-
List these intermolecular interactions from weakest to strongest: covalent network bonding, dipole-dipole interactions, and dispersion forces.
-
What type of intermolecular interaction is predominate in each substance?
- water (H2O)
- sodium sulfate (Na2SO4)
- decane (C10H22)
-
What type of intermolecular interaction is predominate in each substance?
- diamond (C, crystal)
- helium (He)
- ammonia (NH3)
-
Explain how a molecule like carbon dioxide (CO2) can have polar covalent bonds but be nonpolar overall.
-
Sulfur dioxide (SO2) has a formula similar to that of carbon dioxide (see Exercise 7) but is a polar molecule overall. What can you conclude about the shape of the SO2 molecule?
-
What are some of the physical properties of substances that experience covalent network bonding?
-
What are some of the physical properties of substances that experience only dispersion forces?
Answers
-
solid, liquid, and gas
-
London forces, hydrogen bonding, and ionic interactions
-
- hydrogen bonding
- ionic interactions
- dispersion forces
-
The two covalent bonds are oriented in such a way that their dipoles cancel out.
9. very hard, high melting point
10. very soft, very low melting point
8.2: Solids and Liquids
Concept Review Exercise
-
How do the strengths of intermolecular interactions in solids and liquids differ?
Answer
-
Solids have stronger intermolecular interactions than liquids do.
Exercises
-
What are the general properties of solids?
-
What are the general properties of liquids
-
What are the general properties of gases?
-
What phase or phases have a definite volume? What phase or phases do not have a definite volume?
-
Name a common substance that forms a crystal in its solid state.
-
Name a common substance that forms an amorphous solid in its solid state.
-
Are substances with strong intermolecular interactions likely to be solids at higher or lower temperatures? Explain.
-
Are substances with weak intermolecular interactions likely to be liquids at higher or lower temperatures? Explain.
-
State two similarities between the solid and liquid states.
-
State two differences between the solid and liquid states.
-
If individual particles are moving around with respect to each other, a substance may be in either the _______ or ________ state but probably not in the _______ state.
-
If individual particles are in contact with each other, a substance may be in either the ______ or _______ state but probably not in the ______ state.
Answers
-
hard, specific volume and shape, high density, cannot be compressed
-
variable volume and shape, low density, compressible
-
sodium chloride (answers will vary)
-
At higher temperatures, their intermolecular interactions are strong enough to hold the particles in place.
-
high density; definite volume
11. liquid; gas; solid
12. solid; liquid; gas
8.3: Gases and Pressure
Concept Review Exercise
-
What is pressure, and what units do we use to express it?
Answer
-
Pressure is the force per unit area; its units can be pascals, torr, millimeters of mercury, or atmospheres.
Exercises
-
What is the kinetic theory of gases?
-
According to the kinetic theory of gases, the individual gas particles are (always, frequently, never) moving.
-
Why does a gas exert pressure?
-
Why does the kinetic theory of gases allow us to presume that all gases will show similar behavior?
-
Arrange the following pressure quantities in order from smallest to largest: 1 mmHg, 1 Pa, and 1 atm.
-
Which unit of pressure is larger—the torr or the atmosphere?
-
How many torr are there in 1.56 atm?
-
Convert 760 torr into pascals.
-
Blood pressures are expressed in millimeters of mercury. What would be the blood pressure in atmospheres if a patient’s systolic blood pressure is 120 mmHg and the diastolic blood pressure is 82 mmHg? (In medicine, such a blood pressure would be reported as “120/82,” spoken as “one hundred twenty over eighty-two.”)
-
In weather forecasting, barometric pressure is expressed in inches of mercury (in. Hg), where there are exactly 25.4 mmHg in every 1 in. Hg. What is the barometric pressure in millimeters of mercury if the barometric pressure is reported as 30.21 in. Hg?
Answers
-
Gases are composed of tiny particles that are separated by large distances. Gas particles are constantly moving, experiencing collisions with other gas particles and the walls of their container. The velocity of gas particles is related to the temperature of a gas. Gas particles do not experience any force of attraction or repulsion with each other.
-
A gas exerts pressure as its particles rebound off the walls of its container.
-
1 Pa, 1 mmHg, and 1 atm
-
1,190 torr
9. 0.158 atm; 0.108 atm
10. 767.3 mm Hg
8.4: Gas Laws
Concept Review Exercises
- What properties do the gas laws help us predict?
- What makes the ideal gas law different from the other gas laws?
Answers
- Gas laws relate four properties: pressure, volume, temperature, and number of moles.
- The ideal gas law does not require that the properties of a gas change.
Exercises
-
What conditions of a gas sample should remain constant for Boyle’s law to be used?
-
What conditions of a gas sample should remain constant for Charles’s law to be used?
-
Does the identity of a gas matter when using Boyle’s law? Why or why not?
-
Does the identity of a gas matter when using Charles’s law? Why or why not?
-
A sample of nitrogen gas is confined to a balloon that has a volume of 1.88 L and a pressure of 1.334 atm. What will be the volume of the balloon if the pressure is changed to 0.662 atm? Assume that the temperature and the amount of the gas remain constant.
-
A sample of helium gas in a piston has a volume of 86.4 mL under a pressure of 447 torr. What will be the volume of the helium if the pressure on the piston is increased to 1,240 torr? Assume that the temperature and the amount of the gas remain constant.
-
If a gas has an initial pressure of 24,650 Pa and an initial volume of 376 mL, what is the final volume if the pressure of the gas is changed to 775 torr? Assume that the amount and the temperature of the gas remain constant.
-
A gas sample has an initial volume of 0.9550 L and an initial pressure of 564.5 torr. What would the final pressure of the gas be if the volume is changed to 587.0 mL? Assume that the amount and the temperature of the gas remain constant.
-
A person draws a normal breath of about 1.00 L. If the initial temperature of the air is 18°C and the air warms to 37°C, what is the new volume of the air? Assume that the pressure and amount of the gas remain constant.
-
A person draws a normal breath of about 1.00 L. If the initial temperature of the air is −10°C and the air warms to 37°C, what is the new volume of the air? Assume that the pressure and the amount of the gas remain constant.
-
An air/gas vapor mix in an automobile cylinder has an initial temperature of 450 K and a volume of 12.7 cm3. The gas mix is heated to 565°C. If pressure and amount are held constant, what is the final volume of the gas in cubic centimeters?
-
Given the following conditions for a gas: Vi = 0.665 L, Ti = 23.6°C, Vf = 1.034 L. What is Tf in degrees Celsius and kelvins?
-
Assuming the amount remains the same, what must be the final volume of a gas that has an initial volume of 387 mL, an initial pressure of 456 torr, an initial temperature of 65.0°C, a final pressure of 1.00 atm, and a final temperature of 300 K?
-
When the nozzle of a spray can is depressed, 0.15 mL of gas expands to 0.44 mL, and its pressure drops from 788 torr to 1.00 atm. If the initial temperature of the gas is 22.0°C, what is the final temperature of the gas?
-
Use the ideal gas law to show that 1 mol of a gas at STP has a volume of about 22.4 L.
-
Use a standard conversion factor to determine a value of the ideal gas law constant R that has units of L•torr/mol•K.
-
How many moles of gas are there in a 27.6 L sample at 298 K and a pressure of 1.44 atm?
-
How many moles of gas are there in a 0.066 L sample at 298 K and a pressure of 0.154 atm?
-
A 0.334 mol sample of carbon dioxide gas is confined to a volume of 20.0 L and has a pressure of 0.555 atm. What is the temperature of the carbon dioxide in kelvins and degrees Celsius?
-
What must V be for a gas sample if n = 4.55 mol, P = 7.32 atm, and T = 285 K?
21. What is the pressure of 0.0456 mol of Ne gas contained in a 7.50 L volume at 29°C?
22. What is the pressure of 1.00 mol of Ar gas that has a volume of 843.0 mL and a temperature of −86.0°C?
23. A mixture of the gases \(N_2\), \(O_2\), and \(Ar\) has a total pressure of 760 mm Hg. If the partial pressure of \(N_2\) is 220 mm Hg and of \(O_2\) is 470 mm Hg, What is the partial pressure of \(Ar\)?
24. What percent of the gas above is Ar?
25. Apply Henry’s Law to the diagram below to explain:
why oxygen diffuses from the alveoli of the lungs into the blood and from the blood into the tissues of the body. why carbon dioxide diffuses from the tissues into the blood and from the blood into the alveoli and then finally out into the atmosphere.
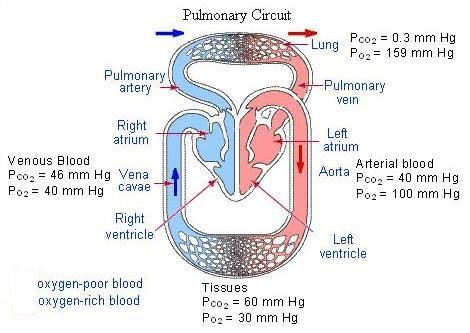
Answers
-
temperature and amount of the gas
6. 31.1 mL
7. 92.1 mL
8. 918.4 torr
9. 1.07 L
10. 1.18 L
11. 23.7 cm3
12. 461 K; 1880C
13. 206 mL
14. 835 K; 5620C
15. The ideal gas law confirms that 22.4 L equals 1 mol.
16. \(\dfrac{760\: torr}{1\: atm}\)
17. 1.63 mol
18. 4.2 x 10-4 mol
19. 405 K; 132°C
20. 14.5 L
21. 0.151 atm
22. 18.2 atm
23. 70 mm Hg
24. 9.2%
25. Gases diffuse from high concentration to low concentration (Henry's Law). The partial pressure of oxygen is high in the alveoli and low in the blood of the pulmonary capillaries. As a result, oxygen diffuses across the respiratory membrane from the alveoli into the blood. It's also higher partial pressure in the blood than in the tissues, hence it transfers to the tissues. On the other hand, carbon dioxide diffuses from the tissues (highest CO2 partial pressure) and across the respiratory membrane from the blood into the alveoli and out to the atmosphere.
Additional Exercises
-
How many grams of oxygen gas are needed to fill a 25.0 L container at 0.966 atm and 22°C?
-
A breath of air is about 1.00 L in volume. If the pressure is 1.00 atm and the temperature is 37°C, what mass of air is contained in each breath? Use an average molar mass of 28.8 g/mol for air.
-
The balanced chemical equation for the combustion of propane is as follows:
\[C_3H_{8(g)} + 5O_{2(g)} \rightarrow 3CO_{2(g)} + 4H_2O_{(ℓ)}\]
- If 100.0 g of propane are combusted, how many moles of oxygen gas are necessary for the reaction to occur?
- At STP, how many liters of oxygen gas would that be?
-
The equation for the formation of ammonia gas (NH3) is as follows:
\[N_{2(g)} + 3H_{2(g)} \rightarrow 2NH_{3(g)}\]
At 500°C and 1.00 atm, 10.0 L of N2 gas are reacted to make ammonia.
- If the pressures and temperatures of H2 and NH3 were the same as those of N2, what volume of H2 would be needed to react with N2, and what volume of NH3 gas would be produced?
- Compare your answers to the balanced chemical equation. Can you devise a “shortcut” method to answer Exercise 4a?
-
At 20°C, 1 g of liquid H2O has a volume of 1.002 mL. What volume will 1 g of water vapor occupy at 20°C if its pressure is 17.54 mmHg? By what factor has the water expanded in going from the liquid phase to the gas phase?
-
At 100°C, 1 g of liquid H2O has a volume of 1.043 mL. What volume will 1 g of steam occupy at 100°C if its pressure is 760.0 mmHg? By what factor has the water expanded in going from the liquid phase to the gas phase?
-
Predict whether NaCl or NaI will have the higher melting point. Explain. (Hint: consider the relative strengths of the intermolecular interactions of the two compounds.)
-
Predict whether CH4 or CH3OH will have the lower boiling point. Explain. (Hint: consider the relative strengths of the intermolecular interactions of the two compounds.)
-
A standard automobile tire has a volume of about 3.2 ft3 (where 1 ft3 equals 28.32 L). Tires are typically inflated to an absolute pressure of 45.0 pounds per square inch (psi), where 1 atm equals 14.7 psi. Using this information with the ideal gas law, determine the number of moles of air needed to fill a tire if the air temperature is 18.0°C.
-
Another gas law, Amontons’s law, relates pressure and temperature under conditions of constant amount and volume:
\(\mathrm{\dfrac{P_i}{T_i}=\dfrac{P_f}{T_f}}\)
If an automobile tire (see Exercise 9) is inflated to 45.0 psi at 18.0°C, what will be its pressure if the operating temperature (i.e., the temperature the tire reaches when the automobile is on the road) is 45.0°C? Assume that the volume and the amount of the gas remain constant.
Answers
-
31.9 g
3.
- 11.4 mol
- 255 L
-
57.75 L; an expansion of 57,600 times
-
NaCl; with smaller anions, NaCl likely experiences stronger ionic bonding.
9. 11.6 mol
10. 49.2 psi

