5.4: Atomic Orbitals and Magnetism

The MO picture we developed in Section 6.4 helps us rationalize the electrical conductivity of Na (3s¹), but what about Mg, which (as an atom in the gas phase) has a 3s² electronic configuration? The two valence electrons are spin-paired in atomic Mg, as they are in the helium atom (1s²). When the 3s orbitals of Mg combine to form a band, we would expect the band to be completely filled, since Mg has two electrons per orbital. By this reasoning, solid Mg should be an insulator. But Mg has all the properties of a metal: high electrical and thermal conductivity, metallic luster, malleability, etc. In this case the 3s and 3p bands are sufficiently broad (because of strong orbital overlap between Mg atoms) that they form a continuous band. This band, which contains a total of four orbitals (one 3s and three 3p) per atom, is only partially filled by the two valence electrons.

Another way to think about this is to consider the hybridization of the 3s and 3p electrons in Mg. Hybridization requires promotion from the 3s²3p⁰ ground state of an Mg atom to a 3s¹3p¹ excited state. The promotion energy (+264 kJ/mol) is more than offset by the bonding energy (-410 kJ/mol), the energy released when gaseous atoms in the excited state condense to form the metallic solid. The heat of vaporization, or the cohesive energy of a metal, is the difference between the bonding energy and the promotion energy. Experimentally, we can measure the vaporization energy (+146 kJ/mol) and the promotion energy and use them to calculate the bonding energy. From this we learn that each s or p electron is worth about 200 kJ/mol in bonding energy. The concepts of promotion energy and bonding energy are very useful in rationalizing periodic trends in the bond strengths and magnetic properties of metals, which are described below.

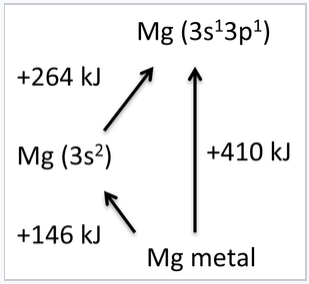
The cohesive energy of Mg metal is the difference between the bonding and promotion energies. The ground state of a gas phase Mg atom is [Ar]3s^2, but it can be promoted to the [Ar]3s^13p^1 state, which is 264 kJ/mol above the ground state. Mg uses two electrons per atom to make bonds, and the sublimation energy of the metal is 146 kJ/mol.

Filling of the 3d and 4s,4p bands

In the 3d series, we see magnetic behavior for elements and alloys between Cr and Ni. Past Ni, the elements (Cu, Zn, Ga,...) are no longer magnetic and they are very good electrical conductors, implying that their valence electrons are highly delocalized. We can understand this behavior by considering the overlap of 4s, 4p, and 3d orbitals, all of which are close in energy. The 4s and 4p have strong overlap and form a broad, continuous band. On the other hand, the 3d electrons are contracted and form a relatively narrow band. Progressing from the early 3d elements (Sc, Ti, V), we begin to fill the 3d orbitals, which are not yet so contracted that they cannot contribute to bonding. Thus, the valence electrons in Sc, Ti, and V are all spin-paired, except for a small number near the Fermi level that give rise to a weak Pauli paramagnetism. Moving across the 3d series to the magnetic elements (Fe, Co, Ni), the d-orbitals are now so contracted that their electrons unpair and we see cooperative ordering of spins (ferromagnetism and antiferromagnetism). Referring to the band diagram at the right, the 3d band is only partially filled and the Fermi level cuts through it. For Cu, Zn, and Ga, the 3d orbitals are even more contracted and the 3d band is thus more narrow, but now it is completely filled and the Fermi level is in the 4s,4p band. The strong orbital overlap in these bands results in spin pairing and a high degree of electron delocalization. Consequently, metals in this part of the periodic table (Cu, Ag) are diamagnetic and are among the best electrical conductors at room temperature. Finally, at Ge, the 4s,4p band is completely filled and the solid is a semiconductor.

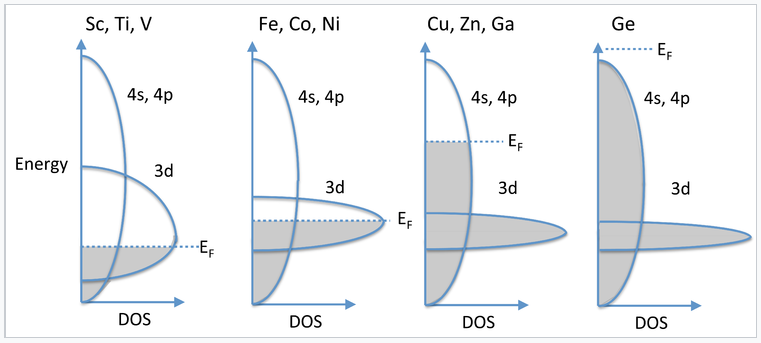
Progressive filling of the 3d and 4s,4p bands going across the periodic table from Sc to Ge.

Materials are classified as diamagnetic if they contain no unpaired electrons. Diamagnetic substances are very weakly repelled from an inhomogeneous magnetic field. Molecules or ions that have unpaired spins are paramagnetic and are attracted to a magnet, i.e., they move towards the high field region of an inhomogeneous field. This attractive force results from the alignment of spins with the field, but in the case of paramagnetism each molecule acts independently. In metals, alloys, oxides, and other solid state compounds, the unpaired spins interact strongly with each other and can order spontaneously, resulting in the cooperative magnetic phenomena described below.