1.2.3.4.1: Quantitative Measures of Hardness, Softness, and Acid-Base Interactions from a Hard Soft Acid-Base Principle perspective involve orbital energies and or apportioning acid-base bonding in terms of electrostatic and covalent factors

Pearson Absolute Hardness is a useful metric of hardness based on orbital energies

The recognition that hard acids and bases possess a large HOMO-LUMO gap suggests that the gap size itself might serve as a useful index of hardness. The basis for this idea may be found by considering Pearson’s definition of absolute hardness, η.¹ Pearson's absolute hardness, η, is half the second derivative of a species' energy with respect to changes in total number of electrons, \(N_{e^-}\).

\[\text{Pearson’s absolute hardness} = η = \dfrac{1}{2} \dfrac{d^2 E}{dN_{e^-}^2} \nonumber \]

\((in~~eV)\)

and, since acids' and bases’ hardness and softness are inversely related, Pearson’s absolute softness, σ, is just the inverse of hardness.

\[\text{Pearson’s softness} = \dfrac{1}{ η} \nonumber \]

Of these, Pearson’s absolute hardness is related to the Mulliken definition of electronegativity as the first derivative of a species' energy with respect to changes in total number of electrons.

\[\text{Mulliken electronegativity} = χ = \dfrac{d E}{dN_{e^-}} \nonumber \]

\((in~~eV)\)

Operationally, both the Pearson hardness and Mulliken electronegativity are approximated in terms of the energies associated with unit changes in the number of electrons – i.e., in terms of ionization energies and electronegativities. Specifically,

\[\text{Pearson’s absolute hardness} = η ≈ \dfrac{IE – EA}{2} \nonumber \]

\[\text{Mulliken electronegativity} = χ ≈ \dfrac{IE + EA}{2} \nonumber \]

where \(IE\) and \(EA\) are in \(eV\).

The connection between Pearson’s absolute hardness/softness and the HOMO-LUMO gap then follows from Koopman’s theorem, in which the ionization energy (IE) is just the opposite of the HOMO energy.

\[IE = -E_{HOMO} \nonumber \]

Similarly, the electron affinity (EA), defined as the opposite of the energy released on absorption of an electron, may be taken as an approximation of the LUMO energy.

\[E_{LUMO} ≈ -EA \nonumber \]

So Pearson’s absolute hardness is just half the HOMO-LUMO gap (band gap) size in electron volts:

\[\text{Pearson's absolute hardness} = η ≈ \dfrac{E_{LUMO} – E_{HOMO}}{2} \nonumber \]

where all values are given in \(eV\),

and the Mulliken electronegativity is just the average of the HOMO and LUMO energies (~Fermi energy):

\[Mulliken~electronegativity, χ ≈ -\dfrac{E_{LUMO} + E_{HOMO}}{2} \nonumber \]

\(where~all~values~are~given~in~eV\)

The relationships between the Pearson absolute hardness, Mulliken electronegativity, and HOMO and LUMO energies are depicted schematically for the group 1A monocations in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\). Relationships between Pearson absolute hardness, Mulliken electronegativity, and HOMO and LUMO energies for the group 1A monocations.

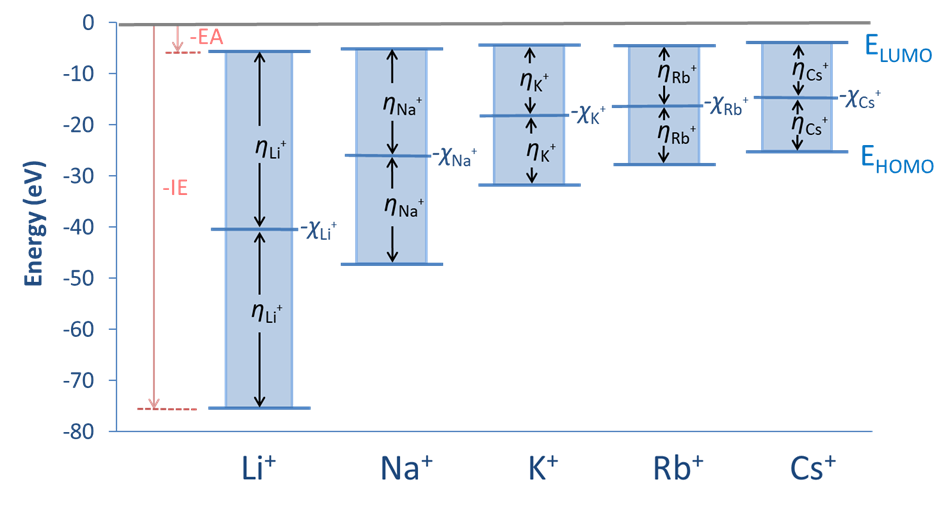
Values of the Pearson hardness and Mulliken electronegativity for several acids and bases are given in Table \(\PageIndex{1}\). The values in the table confirm the expected trends, showing an increase in hardness with size (down a group), with increasing charge, and as substituent electronegativity increases for a series of isolobal ions.

Table \(\PageIndex{1}\): Pearson Absolute Hardness and Related Parameters for Selected Acids and Bases.² Taken from Pearson, R. G., Absolute electronegativity and hardness: application to inorganic chemistry. Inorganic Chemistry 1988, 27 (4), 734-740.

Species	Ionization Energy, IE or I (eV)	Electron Affinity, EA or A (eV)	Mulliken Electronegativity, χ (eV)	Pearson Absolute Hardness, η (eV)
Selected Acids
Group 1A monocations
Li^+	75.64	5.39	40.52	35.12
Na^+	47.29	5.14	26.21	21.08
K^+	31.63	4.34	17.99	13.64
Rb^+	27.28	4.18	15.77	11.55
Cs^+	25.1	3.89	14.5	10.6
Group 11 monocations
Cu^+	20.29	7.73	14.01	6.28
Ag^+	21.49	7.58	14.53	6.96
Au^+	20.5	9.23	14.9	5.6
Isoelectronic Row 3 Metal Cations
Na^+	47.29	5.14	26.21	21.08
Mg^2^+	80.14	15.04	47.59	32.55
Al^3^+	119.99	28.45	74.22	45.77
Changes with Transition Metal Ion Charge
Fe^2^+	30.65	16.18	23.42	7.24
Fe^3^+	54.8	30.65	42.73	12.08
Co^2^+	33.50	17.06	25.28	8.22
Co^3^+	51.3	22.5	42.4	8.9
Boron trihalides
BF3	15.81	-3.5	6.2	9.7
BCl3	11.60	0.33	5.97	5.64
BBr3	10.51	0.82	5.67	4.85
CO2	13.8	-3.8	5.0	8.8
CS2	10.08	0.62	5.35	5.56
Selected Bases
Group 17 monoanions (taken to be identical to the free atom values; for arguments as to why this is reasonable see Pearson, R. G., Inorg. Chem. 1988, 27 (4), 734-740.)
F^-	17.42	3.40	10.41	7.01
Cl^-	13.01	3.62	8.31	4.70
Br^-	11.84	3.36	7.60	4.24
I^-	10.45	3.06	6.76	3.70
Group 15 hydrides
NH3	10.7	-5.6	2.6	8.2
PH3	10.0	-1.9	4.1	6.0
Trimethylpnictides
NMe3	7.8	-4.8	1.5	6.3
PMe3	8.6	-3.1	2.8	5.9
AsMe3	8.7	-2.7	3.0	5.7
Group 16 hydrides
H2O	12.6	-6.4	3.1	9.5
H2S	10.5	-2.1	4.2	6.2
Phosphorous trihalides
PF3	12.3	-1.0	5.7	6.7
PC13	10.2	0.8	5.5	4.7
PBr3	9.9	1.6	5.6	4.2

Drago-Wayland Acid-Base Parameters allow for estimation of the electrostatic and covalent contributions to the enthalpy of formation of a Lewis acid-base adduct.

Although Pearson hardness values are a useful metric of acids' and bases' hardness, they cannot easily be used to estimate the Lewis acid-base interaction energy. This is not the case for the EC model developed by Drago and Wayland.³ In the Drago and Wayland's EC Model, the enthalpy of formation of an acid-base adduct, AB,

\[A + B ⇌ AB ~~~~~~\Delta H_{AB~adduct} \nonumber \]

from the acid (A) and base (B) can be calculated as the sum of products of electrostatic (E) and covalent (C) factors that reflect the propensity of the acid and base to engage in strong electrostatic and covalent interactions with one another:

\[-\Delta H_{AB~adduct} = E_AE_B + C_AC_B \nonumber \]

where E_A and C_A are the electrostatic and covalent parameters for the acid and E_B and C_B the electrostatic and covalent parameters for the base given in units of kcal^½ mol^-½. E and C parameters for selected acids and bases are given in Table \(\PageIndex{2}\) .

Table \(\PageIndex{2}\): E and C Parameters for selected Lewis acids and bases according to the ECW model.^4,5 Taken from Vogel, G. C.; Drago, R. S., The ECW Model. Journal of Chemical Education 1996, 73 (8), 701 and Drago, R. S. A modern approach to acid-base chemistry. Journal of Chemical Education 1974, 51 (5), 300 (for BF₃).

Species	E (kcal^½ mol^-½)	C (kcal^½ mol^-½)	W (kcal mol^-1)	C/E
Acids
I2	0.5^†	2^†	0	4
ICl	2.92	1.66	0	0.57
H2O	1.31	0.78	0	0.59
SO2	0.51	1.56	0	3.1
HCCl3 (chloroform)	1.56	0.44	0	0.28
(CH3)3COH	1.07	0.69	0	0.65
(CF3)3COH	3.06	1.88	-0.87	0.61
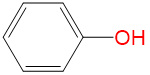	2.27	1.07	0	0.47
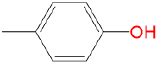	2.23	1.03	0	0.46
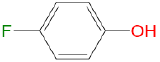	2.30	1.11	0	0.48
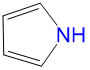	1.38	0.68	0	0.49
BF3	1.62	9.88		6.10
B(CH3)3	2.90	3.60	0	1.2
Al(CH3)3	8.66	3.68	0	0.43
Ga(C2H5)3	6.95	1.48	0	0.21
In(CH3)3	6.60	2.15	0	0.33
Zn[N(Si(CH3)3)]2	2.75	2.32	0	0.84
Cd[N(Si(CH3)3)]2	2.50	1.83	0	0.73
Bases
NH3	2.31	2.04		0.88
CH3NH2	2.16	3.13		1.4
(CH3)2NH	1.80	4.21		2.3
(CH3)3N	1.21	5.61		4.6
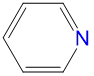	1.78	3.54		2.0
	1.81	3.73		2.0
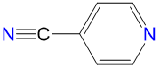	1.53	2.94		1.9
CH3CN	1.64	0.71		0.43
ClCH2CN	1.67	0.33		0.20
CH3C(O)CH3	1.74	1.26		0.72
(C2H5)2O	1.80	1.63		0.91
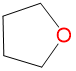	1.64	2.18		1.3
(EtOAc)	1.63	0.95		0.58
	2.35^†	1.31		0.56
(CH3)2S	0.25	3.75		15
(CH3CH2)2S	0.24	3.92^†		15
	0.26	4.07		16
(CH3)2Se	0.05	4.24		83
(CH3)2SO	2.4	1.47		0.61
(CH3)3P	0.25	5.81		24
(CH3O)3P	0.13	4.83		37
(C6H5)3PO	2.59	1.67		0.64
(C6H5)3PS	0.35	3.65		10
C6H6	0.70	0.45		0.64

^{† These values were fixed to parameterize the rest of the E and C parameters.}

Trends in the relative values of C and E for the acids and bases in Table \(\PageIndex{2}\)  are very roughly consistent with the trends in hardness and softness outlined earlier. However, the parameters suggest that some trends in hardness reflect changes in species' ability to engage in ionic interactions while others reflect changes in species' ability to engage in strong covalent interactions. For example, C_B for the dimethylchalcogenides increases steadily from 1.5 to 4.25 kcal^½ mol^-½ on going from Me₂O to Me₂Se while E_B decreases from 1.68 to 0.05 kcal^½ mol^-½, suggesting that electrostatic and covalent factors are both involved in a decrease in base hardness down group 16. However, in the case of phosphines and amines it appears that electrostatic factors are primarily responsible for the decrease in hardness down group 15. On going from Me₃N to Me₃P, C_B only increases slightly from 5.61 to 5.81 kcal^½ mol^-½ while E_B decreases from 1.21 to 0.25 kcal^½ mol^-½ - i.e., to 20% of the Me₃N value.

However, some species tend to have very high values for both E and C, reflecting their ability to engage in strong electrostatic and covalent interactions, while others have small values for both, reflecting their relative stability as free species in solution.

As can be seen by comparing the acids and bases listed in the absolute hardness table (Table \(\PageIndex{1}\)) and the EC parameters table (Table \(\PageIndex{2}\)). The EC model has primarily been applied to organic and main group organometallic acids and bases. However, a variety of extensions have been proposed that enable its wider applicability.

The simple EC model only includes electrostatic and covalent considerations and thus ignores steric, lattice energy, and other contributions to the interaction energy. Thus it is only useful for analyzing the interaction energies of sterically unhindered adducts in which solvation energy and other contributions to the overall interaction energy are insignificant. However, additional refinements of the model attempt to extend its usefulness by accomodating various factors, such as

• Steric strain. Specifically, Hancock and Martell⁶ introduced a D parameter to account for any additional steric strain introduced upon adduct formation,* giving

\[-\Delta H_{AB~adduct} = E_AE_B + C_AC_B - D_AD_B \nonumber \]

• Charge transfer upon adduct formation. As discussed in section 6.4.2, the formation of a Lewis acid-base complex results in a net transfer of electron density from the electron donor (base) to the acceptor (acid). Drago and Wong⁷ extended the EC model to include that charge transfer by adding what they called receptance factors that account for the acid's ability to receive electron density (R_A) and transference factors that account for the base's ability to donate electron density (T_B), giving

\[-\Delta H_{AB~adduct} = E_AE_B + C_AC_B + R_AT_B \nonumber \]

This extension of the EC model is called the electrostatic-covalent-transfer or ECT model. Notably, it has been applied successfully to adducts involving ions, for which the R_AT_B term can account for as much as 31% of the interaction energy.

• Any constant energy term, such as the energy needed to cleave a dimer in order to make the Lewis acid (e.g., Al₂Cl₆ → 2AlCl₃). Drago and Vogel⁴ extended the EC model to accommodate these constant energy terms, which they designated W. The resulting model is called the ECW model, for which

\[-∆H_{AB~adduct} = E_AE_B + C_AC_B + W \nonumber \]

where

\[W = W_A + W_B \nonumber \]

A simple application of EC and extended EC models is that they allow the enthalpy of adduct formation to be calculated. These enthalpy calculations based on the EC model are consistent with the superior interaction energy of hard-hard and soft-soft interactions compared to hard-soft ones. Consider, for example, the transfer of I₂ between BF₃ and InMe₃, H₃N-BF₃, and H₃N-InMe₃.

\[H_3N-BF_3 + InMe_3 ⇌ BF_3 + H_3N-InMe_3 \nonumber \]

Since H₃N is a hard base and BF₃ and InMe₃ are harder and softer acids, respectively, the equilibrium is expected to favor the reactant, H₃N-BF₃. Assuming the equilbrium is enthalpically driven, this qualitative analysis is consistent with the expected endothermic enthalpy of the reaction, as may be seen from the calculated enthalpies of adduct formation for both H₃N-BF₃ and H₃N-InMe₃.

For H₃N-BF₃:

\[-\Delta H_{H_3N-BF_3} = E_{BF_3}E_{NH_3} + C_{BF_3}C_{NH_3} \nonumber \]

\[-\Delta H_{H_3N-BF_3} = (1.62)(2.31) + (9.88)(2.04) \nonumber \]

\[-∆H_{H_3N-BF_3} = 3.74~kcal/mol + 20.1~kcal/mol = 23.8~kcal/mol \nonumber \]

\[∆H_{H_3N-BF_3} = -23.8~kcal/mol \nonumber \]

For H₃N-InMe₃:

\[-∆H_{H_3N-InMe_3} = E_{InMe_3}E_{NH_3} + C_{InMe_3}C_{NH_3} \nonumber \]

\[-∆H_{H_3N-InMe_3} = (6.6)(2.31) + (2.15)(2.04) \nonumber \]

\[-∆H_{H_3N-InMe_3} = 15.25~kcal/mol + 4.39~kcal/mol = 19.63~kcal/mol \nonumber \]

\[∆H_{H_3N-InMe_3} = -19.63~kcal/mol \nonumber \]

So H₃N-BF₃ is enthalpically favored by -4.2 kcal/mol [=-23.8 kcal/mol - (-19.63 kcal/mol) according to Hess' Law].

In addition to their utility for estimating enthalpies of Lewis acid-base complex formation, EC and related models serve as a useful tool for estimating the relative importance of ionic, covalent, and steric factors in complex formation. Specifically,

• The relative contributions of ionic and covalent factors can be calculated directly, as from the E and C terms. This can provide insight into why some complexes are more stable than others. Such calculations reveal that the hard-hard adduct H₃N-BF₃ is favored over the hard-soft adduct H₃N-InMe₃ because of the strong covalent interaction holding together H₃N-BF₃. The covalent term accounts for 84% of the energy of the H₃N-BF₃ interaction and is largely lost upon formation of H₃N-InMe₃, for which it contributes only 22% of the interaction energy. When the electrostatic term is accounted for, it can be seen that the formation of H₃N-InMe₃ from H₃N-BF₃ is disfavored, since it would result in a loss of 15.7 kcal/mol of covalent stabilization that would be incompletely compensated for by a gain of 11.5 kcal/mol of electrostatic stabilization.
• The role of other contributions to the bonding in a Lewis acid-base complex may be estimated from the discrepancy between the experimental and EC model calculated stabilization energies. This is because the EC parameters assume sigma bonding and so any deviation between the calculated and experimental enthalpies of complex formation can be attributed to non-sigma contributions.
  • This is done explicitly in extensions of the EC model. For instance, in the case of the Hancock and Martell, ECT, and ECW extensions of the EC model, the contributions of the steric, charge transfer, and constant energy factors (like dimer dissociation) are directly computed in the model.
  • Comparisons of the difference between the energies calculated using ordinary EC parameters and the observed enthalpies has also been used as an estimate of the
    • steric strain energy in strained adducts, which exhibit a less exothermic heat of adduct formation than expected
    • \(\pi\)-backbonding energy in adducts which are capable of such interactions and exhibit a more exothermic heat of formation than expected.^8-10
  • For examples see (a) Drago, R. S., The interpretation of reactivity in chemical and biological systems with the E and C model. Coordination Chemistry Reviews 1980, 33 (3), 251-277; (b) Drago, R. S.; Bilgrien, C. J., Inductive transfer and coordination of ligands in metal—metal bonded systems. Polyhedron 1988, 7 (16), 1453-1468; (c) Drago, R. S., The question of a synergistic metal-metal interaction leading to .pi.-back-bond stabilization in dirhodium tetrabutyrate adducts. Inorganic Chemistry 1982, 21 (4), 1697-1698.
• The role of electrostatic, covalent, and other contributions to the spectroscopic behavior of Lewis acid-base complexes can be assessed similarly using specialized versions of the ECW or ECT model that allow for calculation of changes in spectroscopic parameters upon adduct formation - e.g., OH stretching frequencies. Details are beyond the scope of this text but may be found in the original literature,¹¹ for example, Drago, R. S.; Vogel, G. C. JACS 1992, 114 (24), 9527-9532; Vogel, G. C.; Drago, R. S., J. Chem. Educ. 1996, 73 (8), 701; Drago, R. S.; Wong, N. M., J. Chem. Educ. 1996, 73 (2), 123.).

Pearson Softness Parameters have been proposed as a means of calculating the equilibrium constant for formation of a Lewis acid-base adduct, although they are more commonly used to estimate metal toxicity

Pearson also proposed a softness parameter that can be used to estimate the thermodynamics of Lewis acid-base complex formation, this time in the form of the equilibrium constant for

\[A + B \overset{K}{⇌} AB \nonumber \]

for which Pearson proposed

\[logK = S_AS_B + \sigma_A \sigma_B \nonumber \]

where S_A and S_B are acid and base parameters related to the strength of the acid-base interaction and \(\sigma_A\) and \(\sigma_B\) are acid and base parameters related to softness. This approach hasn't found as wide an acceptance in studies of chemical reactivity as the Drago-Wayland and absolute hardness parameters. However, because the toxicity of metal ions sometimes depends on their propensity to bind soft Lewis bases in living systems, the softness parameters which Pearson and Mawby subsequently proposed based on the relative energies of metal fluorine and metal iodine bonds¹² have been widely used as a tool for predicting metal ion toxicity.¹³

References

1. Pearson, R. G., Absolute electronegativity and absolute hardness of Lewis acids and bases. Journal of the American Chemical Society 1985, 107 (24), 6801-6806.

2. Pearson, R. G., Absolute electronegativity and hardness: application to inorganic chemistry. Inorganic Chemistry 1988, 27 (4), 734-740.

3. Drago, R. S.; Wayland, B. B., A Double-Scale Equation for Correlating Enthalpies of Lewis Acid-Base Interactions. Journal of the American Chemical Society 1965, 87 (16), 3571-3577.

4. Vogel, G. C.; Drago, R. S., The ECW Model. Journal of Chemical Education 1996, 73 (8), 701.

5. Drago, R. S. A modern approach to acid-base chemistry. Journal of Chemical Education 1974, 51 (5), 300

6. Hancock, R. D.; Martell, A. E., Hard and Soft Acid-Base Behavior in Aqueous Solution: Steric Effects Make Some Metal Ions Hard: A Quantitative Scale of Hardness-Softness for Acids and Bases. Journal of Chemical Education 1996, 73 (7), 654.

7. Drago, R. S.; Wong, N. M., The Role of Electron-Density Transfer and Electronegativity in Understanding Chemical Reactivity and Bonding. Journal of Chemical Education 1996, 73 (2), 123.

8. Drago, R. S., The interpretation of reactivity in chemical and biological systems with the E and C model. Coordination Chemistry Reviews 1980, 33 (3), 251-277.

9. Drago, R. S.; Bilgrien, C. J., Inductive transfer and coordination of ligands in metal—metal bonded systems. Polyhedron 1988, 7 (16), 1453-1468.

10. Drago, R. S., The question of a synergistic metal-metal interaction leading to .pi.-back-bond stabilization in dirhodium tetrabutyrate adducts. Inorganic Chemistry 1982, 21 (4), 1697-1698.

11. Drago, R. S.; Vogel, G. C., Interpretation of spectroscopic changes upon adduct formation and their use to determine electrostatic and covalent (E and C) parameters. Journal of the American Chemical Society 1992, 114 (24), 9527-9532.

12. Pearson, R. G.; Mawby, R. J. The Nature of Metal-Halogen Bonds in Gutmann, V. Halogen Chemistry, vol. 3. Academic Press: London, 1967, pp. 55-84.

13. Kinraide, T. B. Improved Scales for Metal Ion Softness and Toxicity Environmental Toxicology and Chemistry 2009, 28 (3), 525-533.

Notes

* More precisely, the D parameters account for the difference in steric strain in the adduct relative to a water adduct of the Lewis acid.