2.2.0: Nuclear Chemistry and Radioactive Decay
- Page ID
- 210628
Learning Objectives
- Describe nuclear structure in terms of protons, neutrons, and electrons
- Recognize the role of mass defect and binding energy for nuclei in atomic masses
- Explain trends in the relative stability of nuclei
- Identify common particles and energies involved in nuclear reactions
- Write and balance nuclear equations
- Recognize common modes of radioactive decay
- Describe kinetic parameters for decay processes, including half-life
- Describe common radiometric dating techniques
A Review of Isotopes and Introduction to Radioactivity
Video \(\PageIndex{1}\): A video review of isotopes (Unit 2), with a peek at radioactive isotopes.
Nuclear Chemistry - An Introduction
Nuclear chemistry is the study of reactions that involve changes in nuclear structure. The chapter on atoms, molecules, and ions introduced the basic idea of nuclear structure, that the nucleus of an atom is composed of protons and, with the exception of \(\ce{^1_1H}\), neutrons. Recall that the number of protons in the nucleus is called the atomic number (\(Z\)) of the element, and the sum of the number of protons and the number of neutrons is the mass number (\(A\)). Atoms with the same atomic number but different mass numbers are isotopes of the same element. When referring to a single type of nucleus, we often use the term nuclide and identify it by the notation:
\[\ce{^{A}_{Z}X} \label{Eq1}\]
where
- \(X\) is the symbol for the element,
- \(A\) is the mass number, and
- \(Z\) is the atomic number.
Often a nuclide is referenced by the name of the element followed by a hyphen and the mass number. For example, \(\ce{^{14}_6C}\) is called “carbon-14.”
Protons and neutrons, collectively called nucleons, are packed together tightly in a nucleus. With a radius of about 10−15 meters, a nucleus is quite small compared to the radius of the entire atom, which is about 10−10 meters. Nuclei are extremely dense compared to bulk matter, averaging \(1.8 \times 10^{14}\) grams per cubic centimeter. For example, water has a density of 1 gram per cubic centimeter, and iridium, one of the densest elements known, has a density of 22.6 g/cm3. If the earth’s density were equal to the average nuclear density, the earth’s radius would be only about 200 meters (earth’s actual radius is approximately \(6.4 \times 10^6\) meters, 30,000 times larger).
Recall our exploration of atomic size with this video:
Video \(\PageIndex{2}\): An exploration of atomic size. If this video looks familiar its because we also saw it back in Unit 2!
To hold positively charged protons together in the very small volume of a nucleus requires very strong attractive forces because the positively charged protons repel one another strongly at such short distances. The force of attraction that holds the nucleus together is the strong nuclear force. (The strong force is one of the four fundamental forces that are known to exist. The others are the electromagnetic force, the gravitational force, and the nuclear weak force.) This force acts between protons, between neutrons, and between protons and neutrons. It is very different from the electrostatic force that holds negatively charged electrons around a positively charged nucleus (the attraction between opposite charges). Over distances less than 10−15 meters and within the nucleus, the strong nuclear force is much stronger than electrostatic repulsions between protons; over larger distances and outside the nucleus, it is essentially nonexistent.
Nuclear Binding Energy
As a simple example of the energy associated with the strong nuclear force, consider the helium atom composed of two protons, two neutrons, and two electrons. The total mass of these six subatomic particles may be calculated as:
\[ \underset{\Large\text{protons}}{(2 \times 1.0073\; \text{amu})} + \underset{\Large\text{neutrons}}{(2 \times 1.0087\; \text{amu})} + \underset{\Large\text{electrons}}{(2 \times 0.00055\; \text{amu})}= 4.0331\; \text{amu }\label{Eq2}\]
However, mass spectrometric measurements reveal that the mass of an \(\ce{_2^4 He}\) atom is 4.0026 amu, less than the combined masses of its six constituent subatomic particles. This difference between the calculated and experimentally measured masses is known as the mass defect of the atom. In the case of helium, the mass defect indicates a “loss” in mass of 4.0331 amu – 4.0026 amu = 0.0305 amu. The loss in mass accompanying the formation of an atom from protons, neutrons, and electrons is due to the conversion of that mass into energy that is evolved as the atom forms. The nuclear binding energy is the energy produced when the atoms’ nucleons are bound together; this is also the energy needed to break a nucleus into its constituent protons and neutrons. In comparison to chemical bond energies, nuclear binding energies are vastly greater, as we will learn in this section. Consequently, the energy changes associated with nuclear reactions are vastly greater than are those for chemical reactions.
The conversion between mass and energy is most identifiably represented by the mass-energy equivalence equation as stated by Albert Einstein:
\[E=mc^2 \label{Eq3}\]
where E is energy, m is mass of the matter being converted, and c is the speed of light in a vacuum. This equation can be used to find the amount of energy that results when matter is converted into energy. Using this mass-energy equivalence equation, the nuclear binding energy of a nucleus may be calculated from its mass defect, a calculation beyond the scope of our course. A variety of units are commonly used for nuclear binding energies, including electron volts (eV), with 1 eV equaling the amount of energy necessary to the move the charge of an electron across an electric potential difference of 1 volt, making \(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\).
Because the energy changes for breaking and forming bonds are so small compared to the energy changes for breaking or forming nuclei, the changes in mass during all ordinary chemical reactions are virtually undetectable. As we will discuss later in our unit on thermochemistry, the most energetic chemical reactions exhibit enthalpies on the order of thousands of kJ/mol, which is equivalent to mass differences in the nanogram range (10–9 g). On the other hand, nuclear binding energies are typically on the order of billions of kJ/mol, corresponding to mass differences in the milligram range (10–3 g).
Nuclear Stability
A nucleus is stable if it cannot be transformed into another configuration without adding energy from the outside. Of the thousands of nuclides that exist, about 250 are stable. A plot of the number of neutrons versus the number of protons for stable nuclei reveals that the stable isotopes fall into a narrow band. This region is known as the band of stability (also called the belt, zone, or valley of stability). The straight line in Figure \(\PageIndex{1}\) represents nuclei that have a 1:1 ratio of protons to neutrons (n:p ratio). Note that the lighter stable nuclei, in general, have equal numbers of protons and neutrons. For example, nitrogen-14 has seven protons and seven neutrons. Heavier stable nuclei, however, have increasingly more neutrons than protons. For example: iron-56 has 30 neutrons and 26 protons, an n:p ratio of 1.15, whereas the stable nuclide lead-207 has 125 neutrons and 82 protons, an n:p ratio equal to 1.52. This is because larger nuclei have more proton-proton repulsions, and require larger numbers of neutrons to provide compensating strong forces to overcome these electrostatic repulsions and hold the nucleus together.
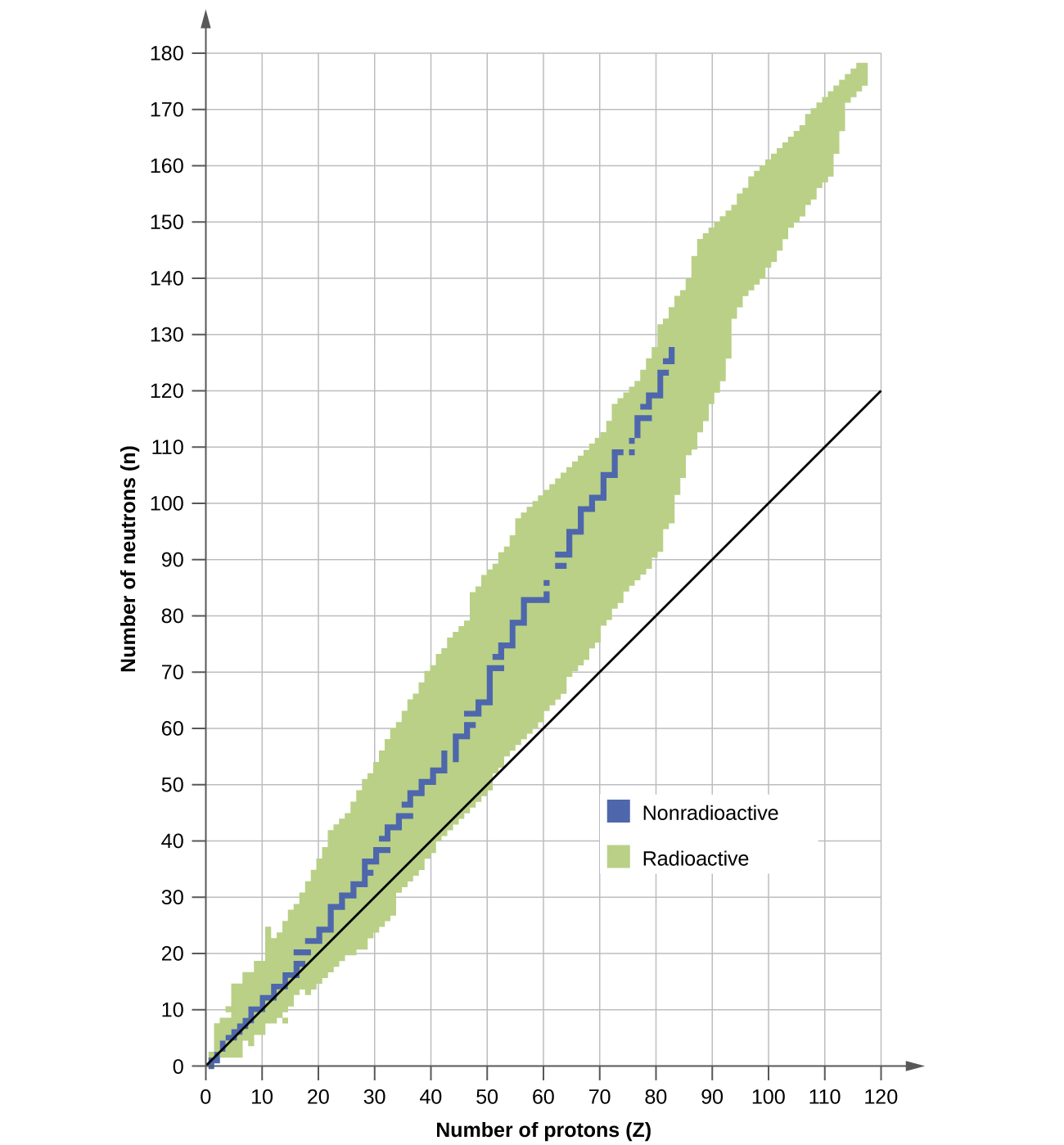
Figure \(\PageIndex{1}\): This plot shows the nuclides that are known to exist and those that are stable. The stable nuclides are indicated in blue, and the unstable nuclides are indicated in green. Note that all isotopes of elements with atomic numbers greater than 83 are unstable. The solid line is the line where n = Z.
The nuclei that are to the left or to the right of the band of stability are unstable and exhibit radioactivity. They change spontaneously (decay) into other nuclei that are either in, or closer to, the band of stability. These nuclear decay reactions convert one unstable isotope (or radioisotope) into another, more stable, isotope. We will discuss the nature and products of this radioactive decay in subsequent sections of this unit.
Several observations may be made regarding the relationship between the stability of a nucleus and its structure. Nuclei with even numbers of protons, neutrons, or both are more likely to be stable (Table \(\PageIndex{1}\)). Nuclei with certain numbers of nucleons, known as magic numbers, are stable against nuclear decay. These numbers of protons or neutrons (2, 8, 20, 28, 50, 82, and 126) make complete shells in the nucleus. These are similar in concept to the stable electron shells observed for the noble gases. Nuclei that have magic numbers of both protons and neutrons, such as \(\ce{^4_2He}\), \(\ce{^{16}_8O}\), \(\ce{^{40}_{20}Ca}\), and \(\ce{^{208}_{82}Pb}\) and are particularly stable. These trends in nuclear stability may be rationalized by considering a quantum mechanical model of nuclear energy states analogous to that used to describe electronic states, which we will discuss later in this course. The details of this model are beyond the scope of this course.
| Number of Stable Isotopes | Proton Number | Neutron Number |
|---|---|---|
| 157 | even | even |
| 53 | even | odd |
| 50 | odd | even |
| 5 | odd | odd |
The relative stability of a nucleus is correlated with its binding energy per nucleon, the total binding energy for the nucleus divided by the number or nucleons in the nucleus. For instance, the binding energy for a \(\ce{^4_2He}\) nucleus is therefore:
\[\mathrm{\dfrac{28.4\; MeV}{4\; nucleons}=7.10\; MeV/nucleon} \label{Eq3a}\]
The binding energy per nucleon of a nuclide on the curve shown in Figure \(\PageIndex{2}\)
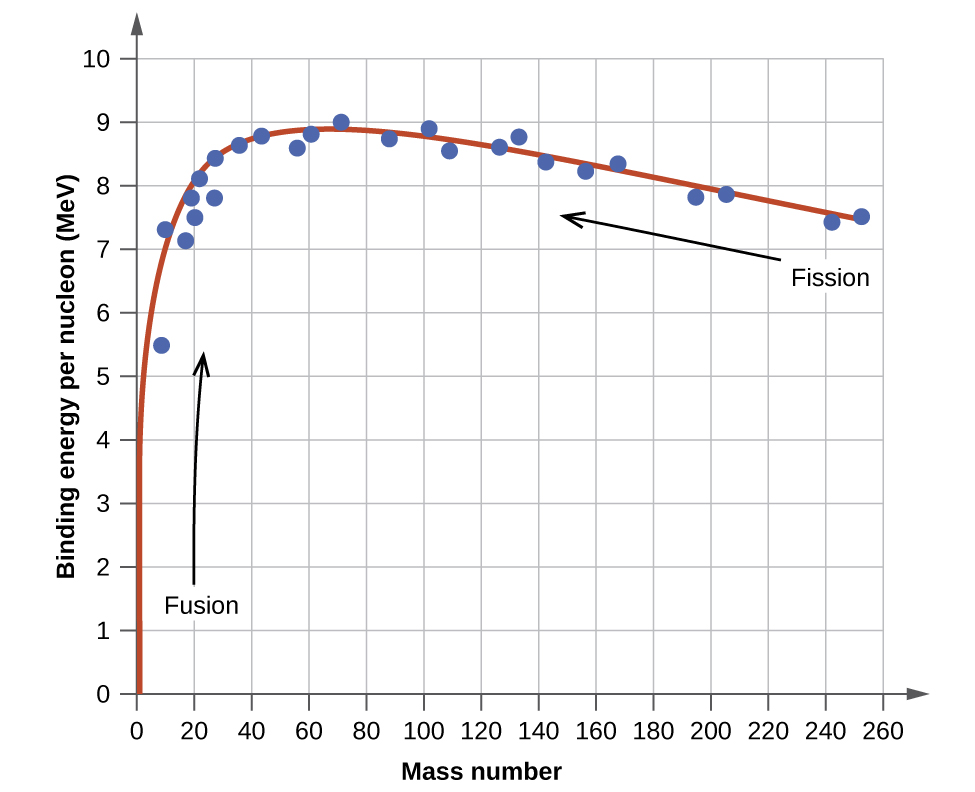
Figure \(\PageIndex{2}\): The binding energy per nucleon is largest for nuclides with mass number of approximately 56.
Changes of nuclei that result in changes in their atomic numbers, mass numbers, or energy states are nuclear reactions. To describe a nuclear reaction, we use an equation that identifies the nuclides involved in the reaction, their mass numbers and atomic numbers, and the other particles involved in the reaction.
Types of Particles in Nuclear Reactions
Video \(\PageIndex{3}\): A brief overview of the different types of radioactivity.
Many entities can be involved in nuclear reactions. The most common are protons, neutrons, alpha particles, beta particles, positrons, and gamma rays, as shown in Figure \(\PageIndex{3}\). Protons \( (\ce{^{1}_{1}p}\), also represented by the symbol \(\ce{^1_1H})\) and neutrons \( (\ce{^1_0n})\) are the constituents of atomic nuclei, and have been described previously. Alpha particles \( (\ce{^4_2He}\), also represented by the symbol \(\ce{^{4}_{2}\alpha})\) are high-energy helium nuclei. Beta particles \( (\ce{^{0}_{−1}\beta}\), also represented by the symbol \(\ce{^0_{-1}e})\) are high-energy electrons, and gamma rays are photons of very high-energy electromagnetic radiation. Positrons \( (\ce{^0_{+1}e}\), also represented by the symbol \(\ce{^0_{+1}β})\) are positively charged electrons (“anti-electrons”). The subscripts and superscripts are necessary for balancing nuclear equations, but are usually optional in other circumstances. For example, an alpha particle is a helium nucleus (He) with a charge of +2 and a mass number of 4, so it is symbolized \(\ce{^4_2He}\). This works because, in general, the ion charge is not important in the balancing of nuclear equations.

Figure \(\PageIndex{3}\): Although many species are encountered in nuclear reactions, this table summarizes the names, symbols, representations, and descriptions of the most common of these.
Note that positrons are exactly like electrons, except they have the opposite charge. They are the most common example of antimatter, particles with the same mass but the opposite state of another property (for example, charge) than ordinary matter. When antimatter encounters ordinary matter, both are annihilated and their mass is converted into energy in the form of gamma rays (γ)—and other much smaller subnuclear particles, which are beyond the scope of this chapter—according to the mass-energy equivalence equation \(E = mc^2\), seen in the preceding section. For example, when a positron and an electron collide, both are annihilated and two gamma ray photons are created:
\[\ce{^0_{−1}e + ^0_{+1}e } \rightarrow \gamma + \gamma \label{21.3.1}\]
Gamma rays compose short wavelength, high-energy electromagnetic radiation and are (much) more energetic than better-known X-rays. Gamma rays are produced when a nucleus undergoes a transition from a higher to a lower energy state, similar to how a photon is produced by an electronic transition from a higher to a lower energy level. Due to the much larger energy differences between nuclear energy shells, gamma rays emanating from a nucleus have energies that are typically millions of times larger than electromagnetic radiation emanating from electronic transitions.
Balancing Nuclear Reactions
A balanced chemical reaction equation reflects the fact that during a chemical reaction, bonds break and form, and atoms are rearranged, but the total numbers of atoms of each element are conserved and do not change. A balanced nuclear reaction equation indicates that there is a rearrangement during a nuclear reaction, but of subatomic particles rather than atoms. Nuclear reactions also follow conservation laws, and they are balanced in two ways:
- The sum of the mass numbers of the reactants equals the sum of the mass numbers of the products.
- The sum of the charges of the reactants equals the sum of the charges of the products.
If the atomic number and the mass number of all but one of the particles in a nuclear reaction are known, we can identify the particle by balancing the reaction. For instance, we could determine that \(\ce{^{17}_8O}\) is a product of the nuclear reaction of \(\ce{^{14}_7N}\) and \(\ce{^4_2He}\) if we knew that a proton, \(\ce{^1_1H}\), was one of the two products. Example \(\PageIndex{1}\) shows how we can identify a nuclide by balancing the nuclear reaction.
Example \(\PageIndex{1}\): Balancing Equations for Nuclear Reactions
The reaction of an α particle with magnesium-25 \( (\ce{^{25}_{12}Mg})\) produces a proton and a nuclide of another element. Identify the new nuclide produced.
Solution
The nuclear reaction can be written as:
\[\ce{^{25}_{12}Mg + ^4_2He \rightarrow ^1_1H + ^{A}_{Z}X}\]
where
- \(\ce A\) is the mass number and
- \(\ce Z\) is the atomic number of the new nuclide, \(\ce X\).
Because the sum of the mass numbers of the reactants must equal the sum of the mass numbers of the products:
\[\mathrm{25+4=A+1}\]
so
\[ \mathrm{A=28}\]
Similarly, the charges must balance, so:
\[\mathrm{12+2=Z+1}\]
so
\[\mathrm{Z=13}\]
Check the periodic table: The element with nuclear charge = +13 is aluminum. Thus, the product is \(\ce{^{28}_{13}Al}\).
Exercise \(\PageIndex{1}\)
The nuclide \(\ce{^{125}_{53}I}\) combines with an electron and produces a new nucleus and no other massive particles. What is the equation for this reaction?
- Answer
-
\[\ce{^{125}_{53}I + ^0_{−1}e \rightarrow ^{125}_{52}Te} \nonumber\]
Following are the equations of several nuclear reactions that have important roles in the history of nuclear chemistry:
- The first naturally occurring unstable element that was isolated, polonium, was discovered by the Polish scientist Marie Curie and her husband Pierre in 1898. It decays, emitting α particles: \[\ce{^{212}_{84}Po⟶ ^{208}_{82}Pb + ^4_2He}\]
- The first nuclide to be prepared by artificial means was an isotope of oxygen, 17O. It was made by Ernest Rutherford in 1919 by bombarding nitrogen atoms with α particles: \[\ce{^{14}_7N + ^4_2α⟶ ^{17}_8O + ^1_1H}\]
- James Chadwick discovered the neutron in 1932, as a previously unknown neutral particle produced along with 12C by the nuclear reaction between 9Be and 4He: \[\ce{^9_4Be + ^4_2He⟶ ^{12}_6C + ^1_0n}\]
- The first element to be prepared that does not occur naturally on the earth, technetium, was created by bombardment of molybdenum by deuterons (heavy hydrogen, \(\ce{^2_1H}\)), by Emilio Segre and Carlo Perrier in 1937: \[ \ce{^2_1H + ^{97}_{42}Mo⟶2^1_0n + ^{97}_{43}Tc}\]
- The first controlled nuclear chain reaction was carried out in a reactor at the University of Chicago in 1942. One of the many reactions involved was: \[ \ce{^{235}_{92}U + ^1_0n⟶ ^{87}_{35}Br + ^{146}_{57}La + 3^1_0n}\]
Following the somewhat serendipitous discovery of radioactivity by Becquerel, many prominent scientists began to investigate this new, intriguing phenomenon. Among them were Marie Curie (Video \(\PageIndex{4}\); the first woman to win a Nobel Prize, and the only person to win two Nobel Prizes in different sciences—chemistry and physics), who was the first to coin the term “radioactivity,” and Ernest Rutherford (of gold foil experiment fame), who investigated and named three of the most common types of radiation. During the beginning of the twentieth century, many radioactive substances were discovered, the properties of radiation were investigated and quantified, and a solid understanding of radiation and nuclear decay was developed.
Learn More about Marie Curie's Life & Work
Video \(\PageIndex{4}\): A brief overview of the life and work of Marie Curie.
The spontaneous change of an unstable nuclide into another is radioactive decay. The unstable nuclide is called the parent nuclide; the nuclide that results from the decay is known as the daughter nuclide. The daughter nuclide may be stable, or it may decay itself. The radiation produced during radioactive decay is such that the daughter nuclide lies closer to the band of stability than the parent nuclide, so the location of a nuclide relative to the band of stability can serve as a guide to the kind of decay it will undergo (Figure \(\PageIndex{4}\)).
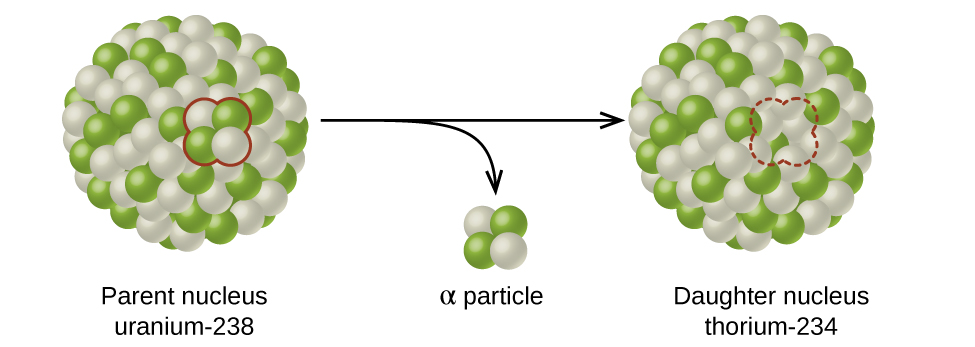
Figure \(\PageIndex{4}\): A nucleus of uranium-238 (the parent nuclide) undergoes α decay to form thorium-234 (the daughter nuclide). The alpha particle removes two protons (green) and two neutrons (gray) from the uranium-238 nucleus.
Although the radioactive decay of a nucleus is too small to see with the naked eye, we can indirectly view radioactive decay in an environment called a cloud chamber. Video \(\PageIndex{5}\) is an opportunity to learn about cloud chambers and to view an interesting Cloud Chamber Demonstration from the Jefferson Lab.
Video \(\PageIndex{5}\): How to Build a Cloud Chamber!
Types of Radioactive Decay
Ernest Rutherford’s experiments involving the interaction of radiation with a magnetic or electric field (Figure \(\PageIndex{5}\)) helped him determine that one type of radiation consisted of positively charged and relatively massive α particles; a second type was made up of negatively charged and much less massive β particles; and a third was uncharged electromagnetic waves, γ rays. We now know that α particles are high-energy helium nuclei, β particles are high-energy electrons, and γ radiation compose high-energy electromagnetic radiation. We classify different types of radioactive decay by the radiation produced.
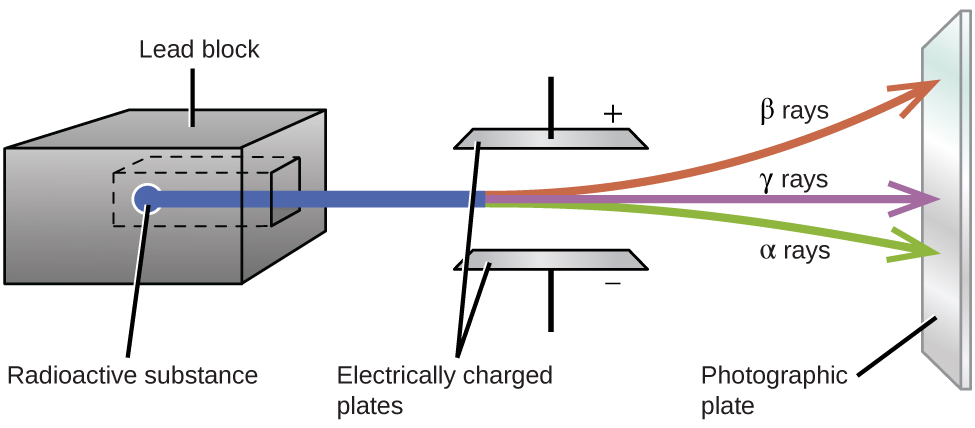
Figure \(\PageIndex{5}\): Alpha particles, which are attracted to the negative plate and deflected by a relatively small amount, must be positively charged and relatively massive. Beta particles, which are attracted to the positive plate and deflected a relatively large amount, must be negatively charged and relatively light. Gamma rays, which are unaffected by the electric field, must be uncharged.
Alpha (α) decay is the emission of an α particle from the nucleus. For example, polonium-210 undergoes α decay:
\[\ce{^{210}_{84}Po⟶ ^4_2He + ^{206}_{82}Pb} \hspace{40px}\ce{or}\hspace{40px} \ce{^{210}_{84}Po ⟶ ^4_2α + ^{206}_{82}Pb}\]
Alpha decay occurs primarily in heavy nuclei (A > 200, Z > 83). Because the loss of an α particle gives a daughter nuclide with a mass number four units smaller and an atomic number two units smaller than those of the parent nuclide, the daughter nuclide has a larger n:p ratio than the parent nuclide. If the parent nuclide undergoing α decay lies below the band of stability, the daughter nuclide will lie closer to the band.
Beta (β) decay is the emission of an electron from a nucleus. Iodine-131 is an example of a nuclide that undergoes β decay:
\[\ce{^{131}_{53}I ⟶ ^0_{-1}e + ^{131}_{54}X} \hspace{40px}\ce{or}\hspace{40px} \ce{^{131}_{53}I ⟶ ^0_{-1}β + ^{131}_{54}Xe}\]
Beta decay, which can be thought of as the conversion of a neutron into a proton and a β particle, is observed in nuclides with a large n:p ratio. The beta particle (electron) emitted is from the atomic nucleus and is not one of the electrons surrounding the nucleus. Such nuclei lie above the band of stability. Emission of an electron does not change the mass number of the nuclide but does increase the number of its protons and decrease the number of its neutrons. Consequently, the n:p ratio is decreased, and the daughter nuclide lies closer to the band of stability than did the parent nuclide.
Gamma emission (γ emission) is observed when a nuclide is formed in an excited state and then decays to its ground state with the emission of a γ ray, a quantum of high-energy electromagnetic radiation. The presence of a nucleus in an excited state is often indicated by an asterisk (*). Cobalt-60 emits γ radiation and is used in many applications including cancer treatment:
\[\mathrm{^{60}_{27}Co^* ⟶\, ^0_0γ +\, ^{60}_{27}Co}\]
There is no change in mass number or atomic number during the emission of a γ ray unless the γ emission accompanies one of the other modes of decay.
Positron emission (β+ decay) is the emission of a positron from the nucleus. Oxygen-15 is an example of a nuclide that undergoes positron emission:
\[\ce{^{15}_8O ⟶ ^0_{+1}e + ^{15}_7N} \hspace{40px}\ce{or}\hspace{40px} \ce{^{15}_8O ⟶ ^0_{+1}β + ^{15}_7N}\]
Positron emission is observed for nuclides in which the n:p ratio is low. These nuclides lie below the band of stability. Positron decay is the conversion of a proton into a neutron with the emission of a positron. The n:p ratio increases, and the daughter nuclide lies closer to the band of stability than did the parent nuclide.
Electron capture occurs when one of the inner electrons in an atom is captured by the atom’s nucleus. For example, potassium-40 undergoes electron capture:
\[\ce{^{40}_{19}K + ^0_{-1}e ⟶ ^{40}_{18}Ar}\]
Electron capture occurs when an inner shell electron combines with a proton and is converted into a neutron. The loss of an inner shell electron leaves a vacancy that will be filled by one of the outer electrons. As the outer electron drops into the vacancy, it will emit energy. In most cases, the energy emitted will be in the form of an X-ray. Like positron emission, electron capture occurs for “proton-rich” nuclei that lie below the band of stability. Electron capture has the same effect on the nucleus as does positron emission: The atomic number is decreased by one and the mass number does not change. This increases the n:p ratio, and the daughter nuclide lies closer to the band of stability than did the parent nuclide. Whether electron capture or positron emission occurs is difficult to predict. The choice is primarily due to kinetic factors, with the one requiring the smaller activation energy being the one more likely to occur. Figure \(\PageIndex{3}\) summarizes these types of decay, along with their equations and changes in atomic and mass numbers.
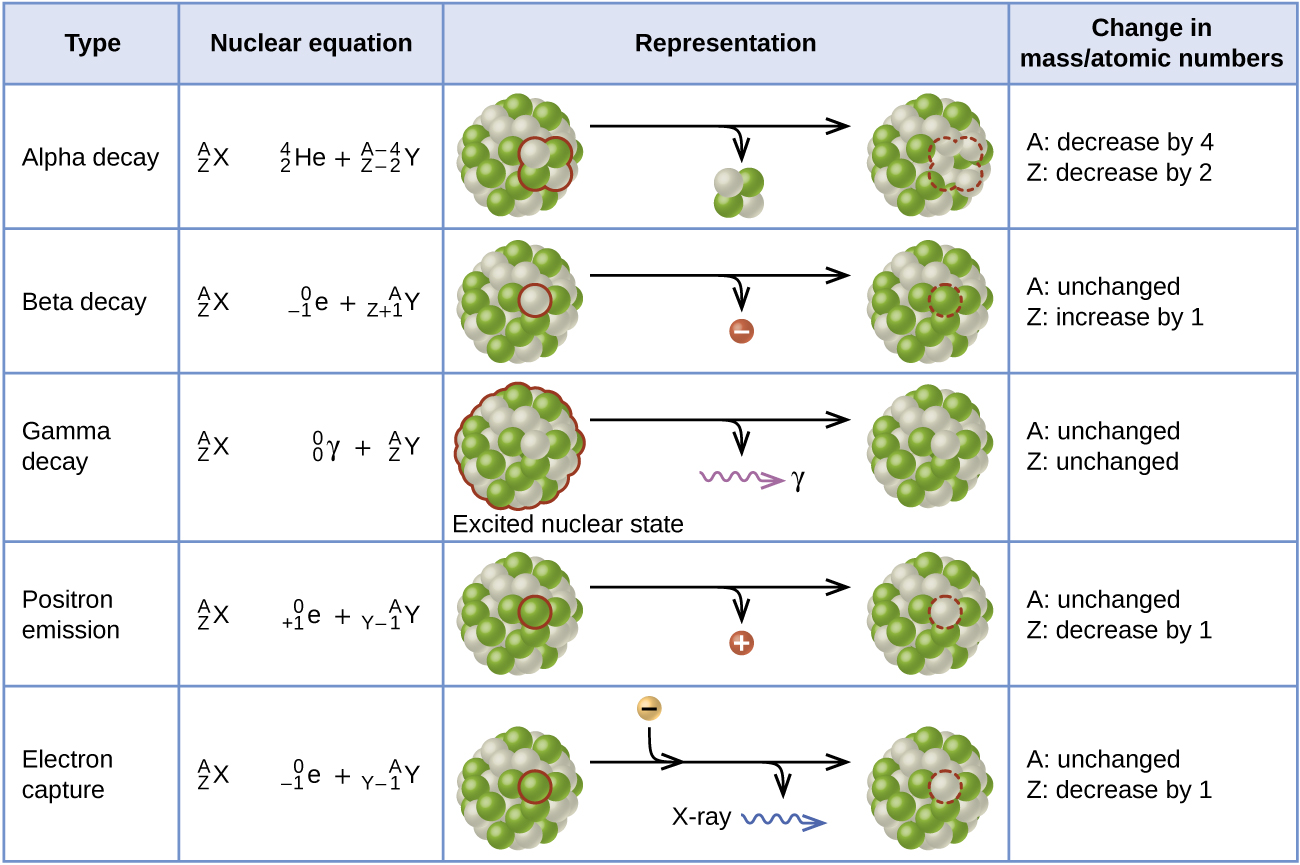
Figure \(\PageIndex{6}\): This table summarizes the type, nuclear equation, representation, and any changes in the mass or atomic numbers for various types of decay.
PET Scan
Positron emission tomography (PET) scans use radiation to diagnose and track health conditions and monitor medical treatments by revealing how parts of a patient’s body function (Figure \(\PageIndex{7}\)). To perform a PET scan, a positron-emitting radioisotope is produced in a cyclotron and then attached to a substance that is used by the part of the body being investigated. This “tagged” compound, or radiotracer, is then put into the patient (injected via IV or breathed in as a gas), and how it is used by the tissue reveals how that organ or other area of the body functions.
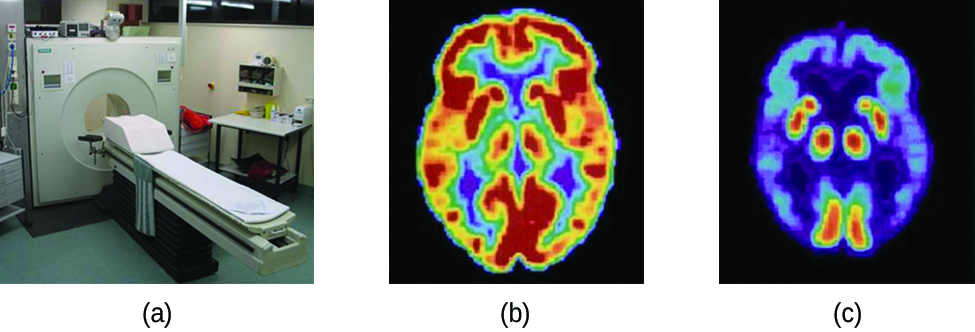
Figure \(\PageIndex{7}\): A PET scanner (a) uses radiation to provide an image of how part of a patient’s body functions. The scans it produces can be used to image a healthy brain (b) or can be used for diagnosing medical conditions such as Alzheimer’s disease (c). (credit a: modification of work by Jens Maus)</
For example, F-18 is produced by proton bombardment of 18O \( (\ce{^{18}_8O + ^1_1p⟶ ^{18}_9F + ^1_0n})\) and incorporated into a glucose analog called fludeoxyglucose (FDG). How FDG is used by the body provides critical diagnostic information; for example, since cancers use glucose differently than normal tissues, FDG can reveal cancers. The 18F emits positrons that interact with nearby electrons, producing a burst of gamma radiation. This energy is detected by the scanner and converted into a detailed, three-dimensional, color image that shows how that part of the patient’s body functions. Different levels of gamma radiation produce different amounts of brightness and colors in the image, which can then be interpreted by a radiologist to reveal what is going on. PET scans can detect heart damage and heart disease, help diagnose Alzheimer’s disease, indicate the part of a brain that is affected by epilepsy, reveal cancer, show what stage it is, and how much it has spread, and whether treatments are effective. Unlike magnetic resonance imaging and X-rays, which only show how something looks, the big advantage of PET scans is that they show how something functions. PET scans are now usually performed in conjunction with a computed tomography scan.
Radioactive Decay Series
The naturally occurring radioactive isotopes of the heaviest elements fall into chains of successive disintegrations, or decays, and all the species in one chain constitute a radioactive family, or radioactive decay series. Three of these series include most of the naturally radioactive elements of the periodic table. They are the uranium series, the actinide series, and the thorium series. The neptunium series is a fourth series, which is no longer significant on the earth because of the short half-lives of the species involved. Each series is characterized by a parent (first member) that has a long half-life and a series of daughter nuclides that ultimately lead to a stable end-product (Figure \(\PageIndex{8}\))—that is, a nuclide on the band of stability (Figure \(\PageIndex{1}\)). In all three series, the end-product is a stable isotope of lead. The neptunium series, previously thought to terminate with bismuth-209, terminates with thallium-205.
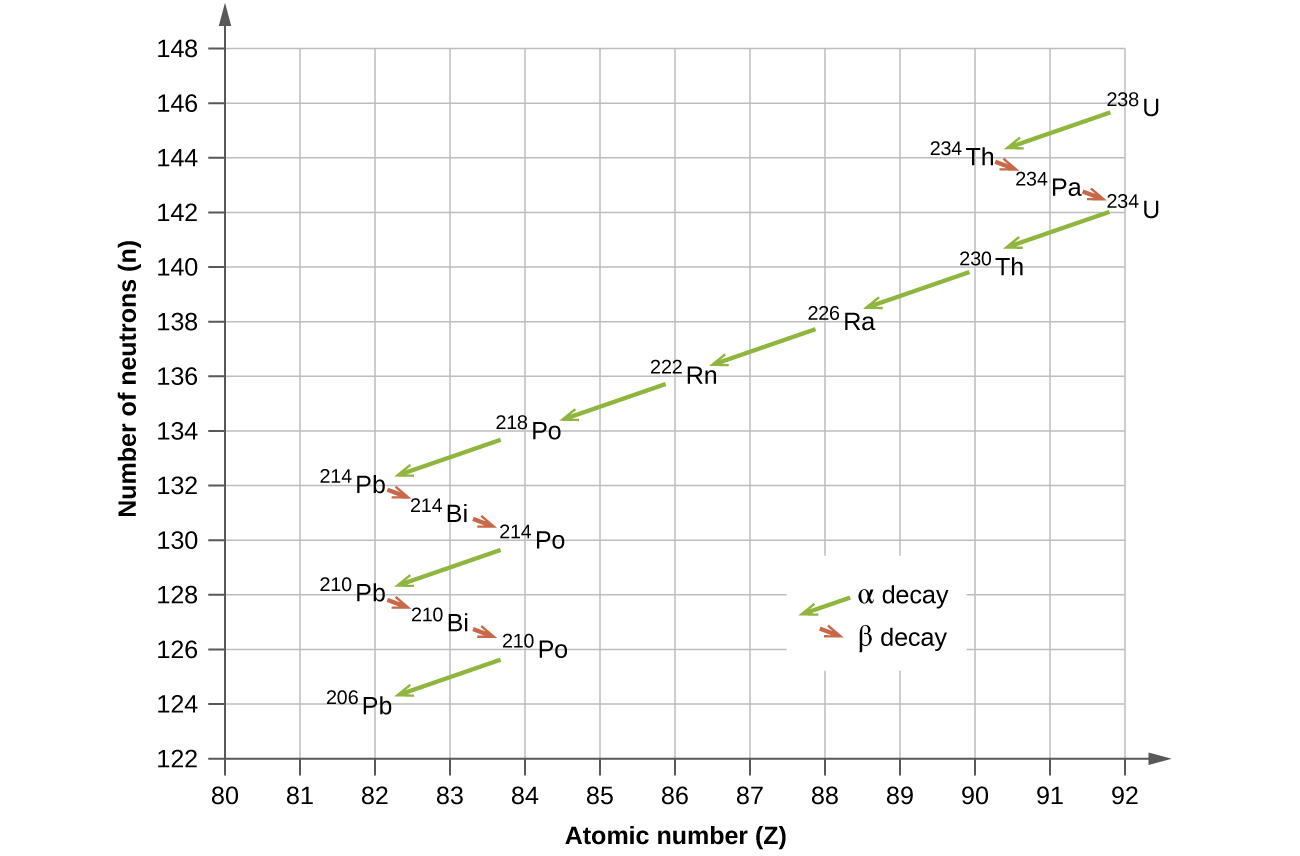
Figure \(\PageIndex{8}\): Uranium-238 undergoes a radioactive decay series consisting of 14 separate steps before producing stable lead-206. This series consists of eight α decays and six β decays.
Radioactive Half-Lives
Radioactive decay follows first-order kinetics. Since first-order reactions have already been covered in detail in the kinetics chapter, we will now apply those concepts to nuclear decay reactions. Each radioactive nuclide has a characteristic, constant half-life (t1/2), the time required for half of the atoms in a sample to decay. An isotope’s half-life allows us to determine how long a sample of a useful isotope will be available, and how long a sample of an undesirable or dangerous isotope must be stored before it decays to a low-enough radiation level that is no longer a problem.
For example, cobalt-60, an isotope that emits gamma rays used to treat cancer, has a half-life of 5.27 years (Figure \(\PageIndex{6}\)). In a given cobalt-60 source, since half of the \(\ce{^{60}_{27}Co}\) nuclei decay every 5.27 years, both the amount of material and the intensity of the radiation emitted is cut in half every 5.27 years. (Note that for a given substance, the intensity of radiation that it produces is directly proportional to the rate of decay of the substance and the amount of the substance.) This is as expected for a process following first-order kinetics. Thus, a cobalt-60 source that is used for cancer treatment must be replaced regularly to continue to be effective.
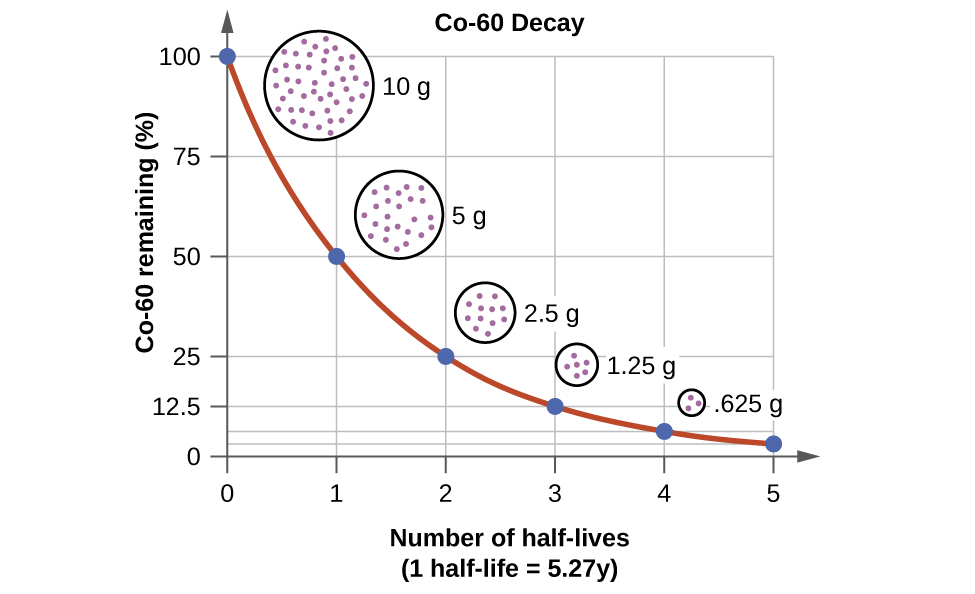
Figure \(\PageIndex{9}\): For cobalt-60, which has a half-life of 5.27 years, 50% remains after 5.27 years (one half-life), 25% remains after 10.54 years (two half-lives), 12.5% remains after 15.81 years (three half-lives), and so on.
Since nuclear decay follows first-order kinetics, we can adapt the mathematical relationships used for first-order chemical reactions. We generally substitute the number of nuclei, N, for the concentration. If the rate is stated in nuclear decays per second, we refer to it as the activity of the radioactive sample. The rate for radioactive decay is:
\[\text{decay rate} = \lambda N\]
with \(\lambda\) is the decay constant for the particular radioisotope.
The decay constant, \(\lambda\), which is the same as a rate constant discussed in the kinetics chapter. It is possible to express the decay constant in terms of the half-life, t1/2:
\[λ=\dfrac{\ln 2}{t_{1/2}}=\dfrac{0.693}{t_{1/2}} \hspace{40px}\ce{or}\hspace{40px} t_{1/2}=\dfrac{\ln 2}{λ}=\dfrac{0.693}{λ}\]
The first-order equations relating amount, N, and time are:
\[N_t=N_0e^{−kt} \hspace{40px}\ce{or}\hspace{40px} t=−\dfrac{1}{λ}\ln\left(\dfrac{N_t}{N_0}\right)\]
where N0 is the initial number of nuclei or moles of the isotope, and Nt is the number of nuclei/moles remaining at time t. We will not concern ourselves with the calculation of half-life in this course.
Because each nuclide has a specific number of nucleons, a particular balance of repulsion and attraction, and its own degree of stability, the half-lives of radioactive nuclides vary widely. For example: the half-life of \(\ce{^{209}_{83}Bi}\) is 1.9 × 1019 years; \(\ce{^{239}_{94}Ra}\) is 24,000 years; \(\ce{^{222}_{86}Rn}\) is 3.82 days; and element-111 (Rg for roentgenium) is 1.5 × 10–3 seconds. The half-lives of a number of radioactive isotopes important to medicine are shown in Table \(\PageIndex{1}\), and others are listed in Appendix N1.
| Type | Decay Mode | Half-Life | Uses |
|---|---|---|---|
| F-18 | β+ decay | 110. minutes | PET scans |
| Co-60 | β decay, γ decay | 5.27 years | cancer treatment |
| Tc-99m1 | γ decay | 8.01 hours | scans of brain, lung, heart, bone |
| I-131 | β decay | 8.02 days | thyroid scans and treatment |
| Tl-201 | electron capture | 73 hours | heart and arteries scans; cardiac stress tests |
| The “m” in Tc-99m stands for “metastable,” indicating that this is an unstable, high-energy state of Tc-99. Metastable isotopes emit \(γ\) radiation to rid themselves of excess energy and become (more) stable. | |||
Radiometric Dating
Several radioisotopes have half-lives and other properties that make them useful for purposes of “dating” the origin of objects such as archaeological artifacts, formerly living organisms, or geological formations. This process is radiometric dating and has been responsible for many breakthrough scientific discoveries about the geological history of the earth, the evolution of life, and the history of human civilization. We will explore some of the most common types of radioactive dating and how the particular isotopes work for each type.
Radioactive Dating Using Carbon-14
The radioactivity of carbon-14 provides a method for dating objects that were a part of a living organism. This method of radiometric dating, which is also called radiocarbon dating or carbon-14 dating, is accurate for dating carbon-containing substances that are up to about 30,000 years old, and can provide reasonably accurate dates up to a maximum of about 50,000 years old.
Naturally occurring carbon consists of three isotopes: \(\ce{^{12}_6C}\), which constitutes about 99% of the carbon on earth; \(\ce{^{13}_6C}\), about 1% of the total; and trace amounts of \(\ce{^{14}_6C}\). Carbon-14 forms in the upper atmosphere by the reaction of nitrogen atoms with neutrons from cosmic rays in space:
\[\ce{^{14}_7N + ^1_0n⟶ ^{14}_6C + ^1_1H}\]
All isotopes of carbon react with oxygen to produce CO2 molecules. The ratio of \(\ce{^{14}_6CO2}\) to \(\ce{^{12}_6CO2}\) depends on the ratio of \(\ce{^{14}_6CO}\) to \(\ce{^{12}_6CO}\) in the atmosphere. The natural abundance of \(\ce{^{14}_6CO}\) in the atmosphere is approximately 1 part per trillion; until recently, this has generally been constant over time, as seen is gas samples found trapped in ice. The incorporation of \(\ce{^{14}_6C ^{14}_6CO2}\) and \(\ce{^{12}_6CO2}\) into plants is a regular part of the photosynthesis process, which means that the \(\ce{^{14}_6C: ^{12}_6C}\) ratio found in a living plant is the same as the \(\ce{^{14}_6C: ^{12}_6C}\) ratio in the atmosphere. But when the plant dies, it no longer traps carbon through photosynthesis. Because \(\ce{^{12}_6C}\) is a stable isotope and does not undergo radioactive decay, its concentration in the plant does not change. However, carbon-14 decays by β emission with a half-life of 5730 years:
\[\ce{^{14}_6C⟶ ^{14}_7N + ^0_{-1}e}\]
Thus, the \(\ce{^{14}_6C: ^{12}_6C}\) ratio gradually decreases after the plant dies. The decrease in the ratio with time provides a measure of the time that has elapsed since the death of the plant (or other organism that ate the plant). Figure \(\PageIndex{10}\) visually depicts this process.

Figure \(\PageIndex{10}\): Along with stable carbon-12, radioactive carbon-14 is taken in by plants and animals, and remains at a constant level within them while they are alive. After death, the C-14 decays and the C-14:C-12 ratio in the remains decreases. Comparing this ratio to the C-14:C-12 ratio in living organisms allows us to determine how long ago the organism lived (and died).
For example, with the half-life of \(\ce{^{14}_6C}\) being 5730 years, if the \(\ce{^{14}_6C : ^{12}_6C}\) ratio in a wooden object found in an archaeological dig is half what it is in a living tree, this indicates that the wooden object is 5730 years old. Highly accurate determinations of \(\ce{^{14}_6C : ^{12}_6C}\) ratios can be obtained from very small samples (as little as a milligram) by the use of a mass spectrometer.
There have been some significant, well-documented changes to the \(\ce{^{14}_6C : ^{12}_6C}\) ratio. The accuracy of a straightforward application of this technique depends on the \(\ce{^{14}_6C : ^{12}_6C}\) ratio in a living plant being the same now as it was in an earlier era, but this is not always valid. Due to the increasing accumulation of CO2 molecules (largely \(\ce{^{12}_6CO2}\)) in the atmosphere caused by combustion of fossil fuels (in which essentially all of the \(\ce{^{14}_6C}\) has decayed), the ratio of \(\ce{^{14}_6C : ^{12}_6C}\) in the atmosphere may be changing. This manmade increase in \(\ce{^{12}_6CO2}\) in the atmosphere causes the \(\ce{^{14}_6C : ^{12}_6C}\) ratio to decrease, and this in turn affects the ratio in currently living organisms on the earth. Fortunately, however, we can use other data, such as tree dating via examination of annual growth rings, to calculate correction factors. With these correction factors, accurate dates can be determined. In general, radioactive dating only works for about 10 half-lives; therefore, the limit for carbon-14 dating is about 57,000 years.
Radioactive Dating Using Nuclides Other than Carbon-14
Radioactive dating can also use other radioactive nuclides with longer half-lives to date older events. For example, uranium-238 (which decays in a series of steps into lead-206) can be used for establishing the age of rocks (and the approximate age of the oldest rocks on earth). Since U-238 has a half-life of 4.5 billion years, it takes that amount of time for half of the original U-238 to decay into Pb-206. In a sample of rock that does not contain appreciable amounts of Pb-208, the most abundant isotope of lead, we can assume that lead was not present when the rock was formed. Therefore, by measuring and analyzing the ratio of U-238:Pb-206, we can determine the age of the rock. This assumes that all of the lead-206 present came from the decay of uranium-238. If there is additional lead-206 present, which is indicated by the presence of other lead isotopes in the sample, it is necessary to make an adjustment. Potassium-argon dating uses a similar method. K-40 decays by positron emission and electron capture to form Ar-40 with a half-life of 1.25 billion years. If a rock sample is crushed and the amount of Ar-40 gas that escapes is measured, determination of the Ar-40:K-40 ratio yields the age of the rock. Other methods, such as rubidium-strontium dating (Rb-87 decays into Sr-87 with a half-life of 48.8 billion years), operate on the same principle. To estimate the lower limit for the earth’s age, scientists determine the age of various rocks and minerals, making the assumption that the earth is older than the oldest rocks and minerals in its crust. As of 2014, the oldest known rocks on earth are the Jack Hills zircons from Australia, found by uranium-lead dating to be almost 4.4 billion years old.
Summary
Video \(\PageIndex{6}\): A video summary of some of the nuclear chemistry you just learned about.
An atomic nucleus consists of protons and neutrons, collectively called nucleons. Although protons repel each other, the nucleus is held tightly together by a short-range, but very strong, force called the strong nuclear force. A nucleus has less mass than the total mass of its constituent nucleons. This “missing” mass is the mass defect, which has been converted into the binding energy that holds the nucleus together according to Einstein’s mass-energy equivalence equation, E = mc2. Of the many nuclides that exist, only a small number are stable. Nuclides with even numbers of protons or neutrons, or those with magic numbers of nucleons, are especially likely to be stable. These stable nuclides occupy a narrow band of stability on a graph of number of protons versus number of neutrons. The binding energy per nucleon is largest for the elements with mass numbers near 56; these are the most stable nuclei.
Nuclei can undergo reactions that change their number of protons, number of neutrons, or energy state. Many different particles can be involved in nuclear reactions. The most common are protons, neutrons, positrons (which are positively charged electrons), alpha (α) particles (which are high-energy helium nuclei), beta (β) particles (which are high-energy electrons), and gamma (γ) rays (which compose high-energy electromagnetic radiation). As with chemical reactions, nuclear reactions are always balanced. When a nuclear reaction occurs, the total mass (number) and the total charge remain unchanged.
Nuclei that have unstable n:p ratios undergo spontaneous radioactive decay. The most common types of radioactivity are α decay, β decay, γ emission, positron emission, and electron capture. Nuclear reactions also often involve γ rays, and some nuclei decay by electron capture. Each of these modes of decay leads to the formation of a new nucleus with a more stable n:p ratio. Some substances undergo radioactive decay series, proceeding through multiple decays before ending in a stable isotope. All nuclear decay processes follow first-order kinetics, and each radioisotope has its own characteristic half-life, the time that is required for half of its atoms to decay. Because of the large differences in stability among nuclides, there is a very wide range of half-lives of radioactive substances. Many of these substances have found useful applications in medical diagnosis and treatment, determining the age of archaeological and geological objects, and more.
Key Equations
- E = mc2
- decay rate = λN
- \(t_{1/2}=\dfrac{\ln 2}{λ}=\dfrac{0.693}{λ}\)
Glossary
- alpha (α) decay
- loss of an alpha particle during radioactive decay
- alpha particle
- (α or \(\ce{^4_2He}\) or \(\ce{^4_2α}\)) high-energy helium nucleus; a helium atom that has lost two electrons and contains two protons and two neutrons
- antimatter
- particles with the same mass but opposite properties (such as charge) of ordinary particles
- band of stability
- (also, belt of stability, zone of stability, or valley of stability) region of graph of number of protons versus number of neutrons containing stable (nonradioactive) nuclides
- beta (β) decay
- breakdown of a neutron into a proton, which remains in the nucleus, and an electron, which is emitted as a beta particle
- beta particle
- (\(β\) or \(\ce{^0_{-1}e}\) or \(\ce{^0_{-1}β}\)) high-energy electron
- binding energy per nucleon
- total binding energy for the nucleus divided by the number of nucleons in the nucleus
- daughter nuclide
- nuclide produced by the radioactive decay of another nuclide; may be stable or may decay further
- electron capture
- combination of a core electron with a proton to yield a neutron within the nucleus
- electron volt (eV)
- measurement unit of nuclear binding energies, with 1 eV equaling the amount energy due to the moving an electron across an electric potential difference of 1 volt
- gamma (γ) emission
- decay of an excited-state nuclide accompanied by emission of a gamma ray
- gamma ray
- (γ or \(\ce{^0_0γ}\)) short wavelength, high-energy electromagnetic radiation that exhibits wave-particle duality
- half-life (t1/2)
- time required for half of the atoms in a radioactive sample to decay
- magic number
- nuclei with specific numbers of nucleons that are within the band of stability
- mass defect
- difference between the mass of an atom and the summed mass of its constituent subatomic particles (or the mass “lost” when nucleons are brought together to form a nucleus)
- mass-energy equivalence equation
- Albert Einstein’s relationship showing that mass and energy are equivalent
- nuclear binding energy
- energy lost when an atom’s nucleons are bound together (or the energy needed to break a nucleus into its constituent protons and neutrons)
- nuclear chemistry
- study of the structure of atomic nuclei and processes that change nuclear structure
- nuclear reaction
- change to a nucleus resulting in changes in the atomic number, mass number, or energy state
- nucleon
- collective term for protons and neutrons in a nucleus
- nuclide
- nucleus of a particular isotope
- parent nuclide
- unstable nuclide that changes spontaneously into another (daughter) nuclide
- positron (\(\ce{^0_{+1}β}\) or \(\ce{^0_{+1}e}\))
- antiparticle to the electron; it has identical properties to an electron, except for having the opposite (positive) charge
- positron emission
- (also, β+ decay) conversion of a proton into a neutron, which remains in the nucleus, and a positron, which is emitted
- radioactive decay
- spontaneous decay of an unstable nuclide into another nuclide
- radioactive decay series
- chains of successive disintegrations (radioactive decays) that ultimately lead to a stable end-product
- radioactivity
- phenomenon exhibited by an unstable nucleon that spontaneously undergoes change into a nucleon that is more stable; an unstable nucleon is said to be radioactive
- radiocarbon dating
- highly accurate means of dating objects 30,000–50,000 years old that were derived from once-living matter; achieved by calculating the ratio of \(\ce{^{14}_6C : ^{12}_6C}\) in the object vs. the ratio of \(\ce{^{14}_6C : ^{12}_6C}\) in the present-day atmosphere
- radioisotope
- isotope that is unstable and undergoes conversion into a different, more stable isotope
- radiometric dating
- use of radioisotopes and their properties to date the formation of objects such as archeological artifacts, formerly living organisms, or geological formations
- strong nuclear force
- force of attraction between nucleons that holds a nucleus together
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Adelaide Clark, Oregon Institute of Technology
- Crash Course Chemistry: Crash Course is a division of Complexly and videos are free to stream for educational purposes.
- TED-Ed’s commitment to creating lessons worth sharing is an extension of TED’s mission of spreading great ideas. Within TED-Ed’s growing library of TED-Ed animations, you will find carefully curated educational videos, many of which represent collaborations between talented educators and animators nominated through the TED-Ed website.
- Fuse School, Open Educational Resource free of charge, under a Creative Commons License: Attribution-NonCommercial CC BY-NC (View License Deed: https://creativecommons.org/licenses/by-nc/4.0/)

