5.4: Isomerism
- Last updated
- Save as PDF
- Page ID
- 344592
This section will be about isomerism in coordination compounds. You may know isomerism already from your organic chemistry classes. Here, we will apply isomerism to coordination chemistry. Some forms of isomerism in organic and coordination chemistry are the same, but there are some forms of isomerism that only occur in coordination chemistry.
Let us first briefly review the definition of isomerism: Isomerism is when two or more compounds have identical empirical formulas but different structures.
Definition: Isomerism
When two or more compounds have identical empirical formulas but different structures they are called isomers.
We distinguish between two basic types of isomerisms: Constitutional isomerism and stereoisomerism. What is the difference? In constitutional isomerism the bonds are not between the same atoms.
Definition: Constitutional Isomers
In constitutional isomers the bonds are not between the same atoms.
In stereoisomerism, the bonds are between the same atoms, but ligands are at different coordination sites.
Definition: Stereoisomers
In stereoisomers, the bonds are between same atoms, but the ligands are at different coordination sites.
Forms of Constitutional Isomerism
Hydrate Isomerism
First, let us look more closely at hydrate isomerism. In hydrate isomerism, in one isomer a water ligand is in the first coordination sphere, and in the other isomer it is in the second coordination sphere. A water molecule in the second coordination sphere is only defined for the solid state, but not in solution. This is because in solution the water molecule would become part of the solvent. Here are a few examples for hydrate isomers.
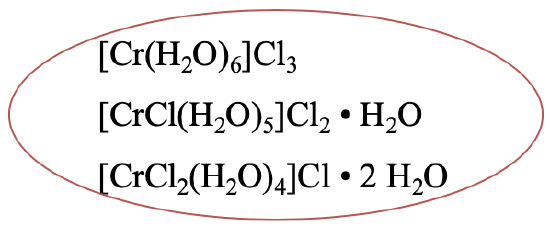
In the complex [Cr(H2O)6]Cl3 there are six aqua ligands in the first coordination sphere (Fig. 5.4.1). In one hydrate isomer, there are only five water molecules in the first coordination sphere, the sixth one is in the second coordination sphere. One chloride anion has moved from the second to the first coordination sphere. There is a third hydrate isomer which has four aqua ligands in the first coordination sphere and two water molecules in the second coordination sphere. Two chloro ligands are now in the first coordination sphere, and one in the second coordination sphere. More hydrate isomers would be possible theoretically, but for some reason nature does not make them.
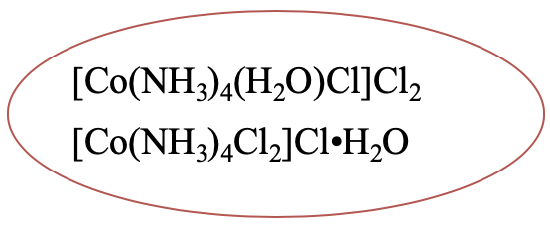
Another example is [Co(NH3)4(H2O)Cl]Cl2. It has a hydrate isomer in which one aqua ligand has moved to the second coordination sphere, and one chloride anion has moved from the second to the first coordination sphere (Fig. 5.4.2).
Ionization Isomerism
A second form of isomerism is the ionization isomerism. In this case an ion moves from the first to the second coordination sphere and/or vice versa.
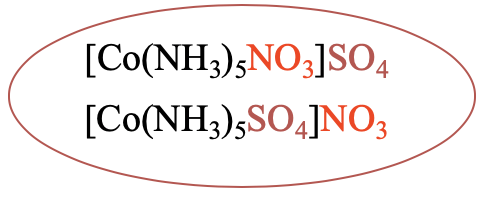
For example, in the compound [Co(NH3)5NO3]SO4 there is a nitrate ion in the first coordination sphere, and a sulfate ion in the second coordination sphere (Fig. 5.4.3). There is an ionization isomer to this compound, in which the sulfate ion is now in the first coordination sphere, and the nitrate is in the second coordination sphere.
Coordination Isomerism
Another form of constitutional isomerism is coordination isomerism. In this isomerism, ligands are bound to different metal ions. Naturally, this implies that this form of isomerism can only exist if at least one isomer has two distinguishable metal ions.
For example, the compound Pt(NH3)2Cl2 has two different coordination isomers. At first glance, they do not seem to be isomers at all. However, we can verify that they have the same empirical formula than the first compound (Fig. 5.4.4).
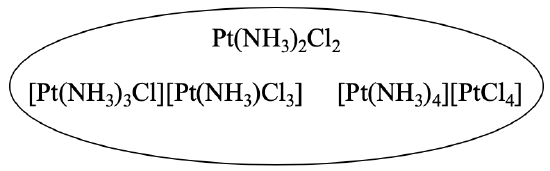
[Pt(NH3)3Cl][Pt(NH3)Cl3] has two Pt atoms, four NH3 units and four Cl atoms. That makes Pt2(NH3)4Cl4. This formula can be divided by 2 to to give Pt(NH3)2Cl2. We can now easily see that the two compounds are isomers. The third isomer also has two Pt atoms, four NH3 units, and four chloro atoms, so it must be an isomer as well.
Why are they coordination isomers? This is because in the first complex all ligands are bound to the same metal atom, whereas in the other two the ligands are bound to different metal atoms. In these compounds, one Pt atom belongs to a complex cation, and the other one to a complex anion. In the second isomer, three ammine ligands and one chloro ligand are bound to the first Pt atom, and one ammine and three chloro ligands are bound to the second Pt atom. In the third isomer, four ammine ligands are bound to the first platinum atom, and four chloro ligands belong to the second platinum atom.
Coordination isomerism is also possible for metal ions of different elements.
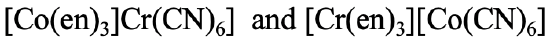
In the example shown (Fig. 5.4.5), the first isomer has ethylenediamine bound to Co and cyanide bound to Cr, whereas in the second isomer ethylenediamine is bound to Cr and the cyano ligand is bound to Co.

Further, in coordination isomers metal ions can be in different oxidation states. We can see that in the two depicted isomers there are complex cations, and complex anions with Pt in in different oxidation states (Fig. 5.4.6). In the first isomer Pt(II) makes the complex cation having four ammine ligands attached to it. Pt(IV) is part of the complex anion being surrounded by six chloro ligands. In the second isomer Pt(IV) forms the complex cation having four ammine and two chloro ligands in the first coordination sphere, and Pt(II) forms the complex anion having four chloro ligands.
Linkage isomerism
Linkage isomerism, also called ambidentate isomerism, is an isomerism that can be observed for ligands that have more than one reactive end. In two linkage isomers, the ligands will bind with different ends to the metal. Which end is reactive depends on the effective HOMO-LUMO interactions. Soft donor atoms tend to bind to soft metals, and hard donor atoms tend to bind to hard metals. Also the solvent can play a big role.
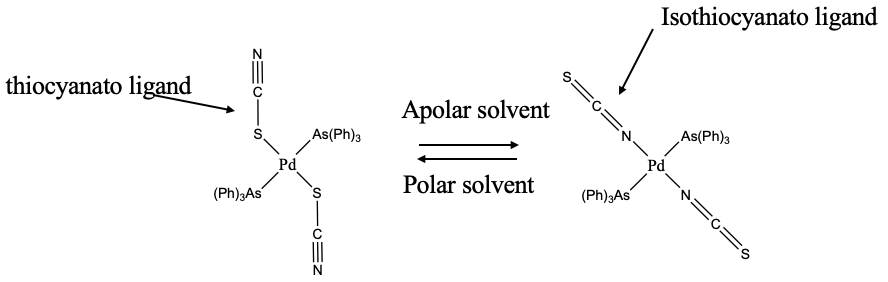
An example of an ambidentate ligand is the thiocyanate anion (Fig. 5.4.7). It can bind either with the sulfur or with the nitrogen end to a metal ion. When it binds with the S-end it is called the thiocyanato-ligand, when it binds with the N-end it is called the isothiocyanato ligand. Which atom binds to the metal can depend on the solvent. In the example shown, thiocyanate binds with S to Pd in polar solvents, but with N in apolar solvents. We could try to rationalize why. A possibility is that in polar solvents the more electronegative N atom can engage in hydrogen bonding which is not possible in apolar solvents. Steric arguments could also play a role. You can see that the triphenyl arsine ligands are fairly bulky. When the ligand binds with the nitrogen, then it binds in linear fashion avoiding steric interference with one of the arsine ligands. So it may be that in apolar solvents steric interactions dominate the behavior, while in polar solvents solvent-ligand interactions are in control.
It is even possible that two, same ambidentate ligands bind with opposite ends to the metal in one and the same molecule.
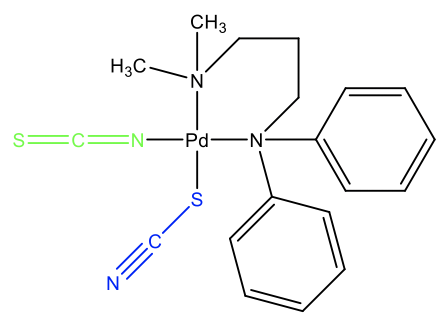
An example is the complex shown (Fig. 5.4.8). In this molecule, there is a thiocyanato and an isocyanato ligand binding to Pd. What arguments would we have to explain this ambidentate isomerism? Think about it for a moment. We can see that the two methyl groups are far less bulky than the two phenyl groups. When thiocyanate binds with the S-atom, then it can bend away from the two bulky phenyl groups. The second thiocyanate anion binds with the N atom because there is no significant interference between the methyl groups and the linear isothiocyanate ligand. This behavior indicates that thermodynamically, the Pd-N interaction is stronger, but only a little bit stronger because other factors such as steric interference can easily reverse the behavior.
Thio- and isothiocyanato ligands are not the only examples of ambidentate ligands.
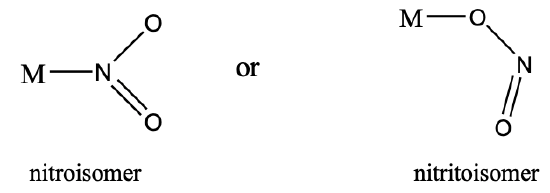
Another example is the nitrite anion. It can either bind with the N- end or the O-end to a metal. In the first case it is called a nitroisomer, in the latter it is called a nitrito isomer (Fig. 5.4.9). Nitritoisomers are usually more stable.
Stereoisomers (Configuration Isomers)
Now let us discuss the second major type of isomerism: Stereisomerism. As mentioned previously, in stereoisomerism the bonds are between the same atoms, but the positions at which the ligands bind, the coordination sites, are different. There are two basic types of stereoisomerism: diastereomerism, and enantiomerism (Fig. 5.4.10).
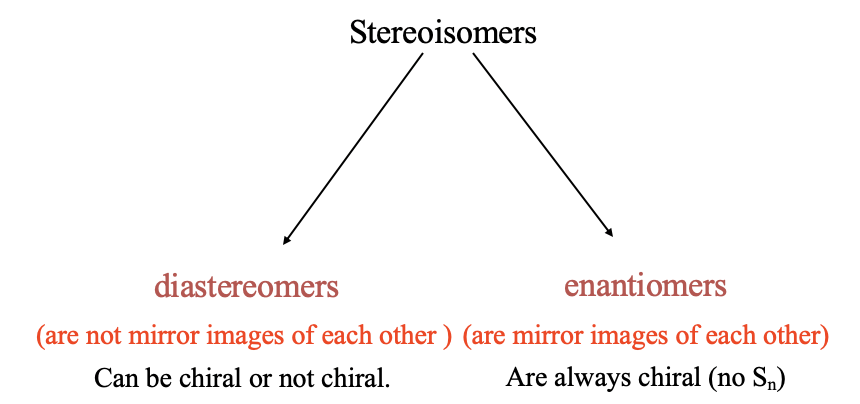
In diastereomerism, the diastereomers are not mirror images to each other.
Definition: Diastereomers
Diastereomers are stereoisomers that are not mirror images of each other. They can be chiral or not chiral.
In enantiomerism, the enantiomers are mirror images to each others. Enantiomers are always chiral molecules.
Definition: Enantiomers
Stereoisomers that are mirror images of each other. They are always chiral.
Diastereomers can be chiral, but do not have to be chiral. Remember, a molecule is chiral when it does not have an improper rotational axis.
Example - Diastereomers and Enantiomers
Let us take an example from organic chemistry to illustrate the difference between enantiomerism and diastereomerism.
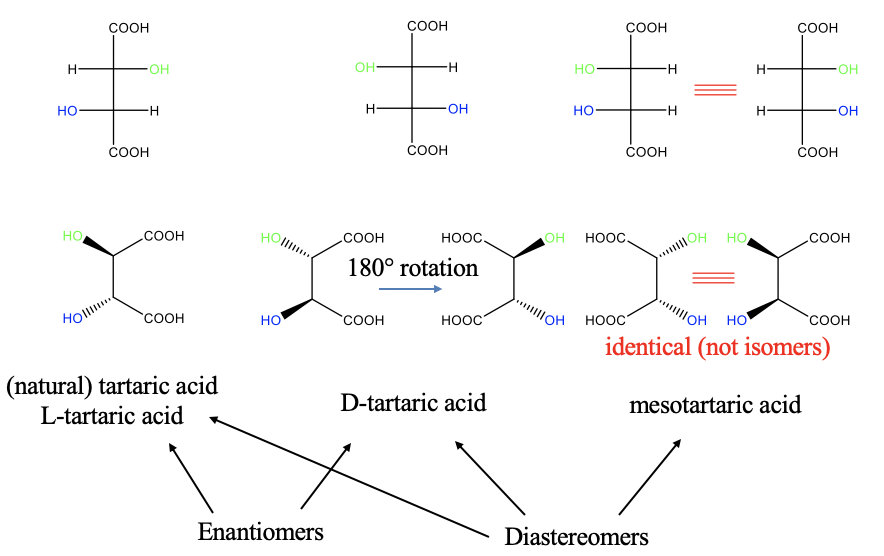
Above (on the top left of Fig. 5.4.11) you see the Fischer projection an isomer of a compound called tartaric acid, it is called L-tartraric acid. The first OH group from the top points to the left, and the second one points to the right. This is the natural form of tartaric acid. The real structure of L-tartaric acid is depicted below (bottom left). You can see the the OH group that points to the right in the Fischer projection points toward us, while the other one, that points to the left in the Fischer projection, points away from us.
In the D-tartaric acid isomer, the first OH group in the Fischer projection points to the left, and the second one points to the right. For the real structure this means that the first OH-group points away from us, and the second one points toward us. These two isomers are mirror images to each other, and thus they are enantiomers. You may not immediately see in the real structure that the two are mirror images, but you can see it when you rotate the molecule around the C-C bond axis so that the carboxylic acid groups point to the the left (Fig. 5.4.11). Can you see it now?
There is a third isomer which is the so-called mesotartraric acid. We can draw its Fischer projection with both OH groups pointing to the right side (Fig. 5.4.11). In the real structure now both hydroxo groups point to the front. Is this molecule a mirror image of one of the two previous molecules? No, it is not! Therefore, it is a diasteromer relative to the other two. At first glance it seems that we can draw another molecule which is the mirror image of the mesotatraric acid. It would have two hydroxo groups pointing to the left in the Fischer projection, and two hydroxo groups pointing away from us in the real structure. However, the two molecules can be rotated so that they superimpose, and therefore they are not isomers, but identical molecules.
Cis-Trans Isomerism
Let us now discuss some common forms of stereoisomerism. The cis-trans isomerism is one very common stereoisomerism. It occurs when two, same ligands are in adjacent or opposite positions. For example, in a square planar complex two ligands can be adjacent or in opposite positions. When in adjacent position, the bond angle is 90° and we have a cis-isomer, when in opposite position, the bond angle is 180° and we have a trans-isomer.
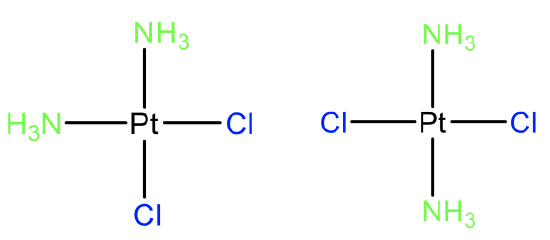
The probably most well known example of a cis-isomer in coordination chemistry is cis-platinum which is an anti-cancer drug (Fig. 5.4.12). Its trans-isomers does not have these pharmaceutical properties showing that cis-trans isomerism can have a profound impact on the properties of a molecule. Overall cis-trans isomerism in Pt(II) complexes have been most intensely studied, but cis-trans isomerism is also known for other d8 metal ions in square planar complexes. We can also ask if cis- and trans isomers are diastereomers or enantiomers. Let us look at the example of cis- and trans-platinum to answer this question. Clearly, these two isomers are not mirror images to each other, so they must be diasteromers. Generally, cis- and trans- isomers are diastereomers.
Cis-trans isomerism extends beyond square planar complexes, and is also known for other shapes, for example, the trigonal bipyramidal shape, and the octahedral shape. In the cis-isomer of an octahedral complex two ligands occupy positions on the same face of the octahedron, whereas in the trans-isomer they occupy opposite position of the octahedron.
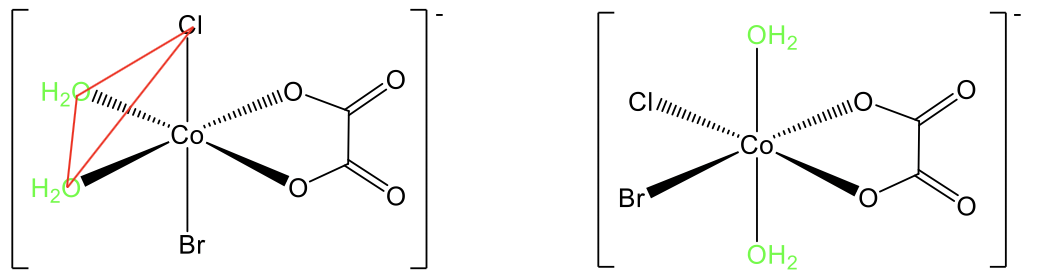
For example, in the complex diaquabromochlorooxalato cobalt(1-) there are cis and trans isomers known (Fig. 5.4.13). In the trans-isomer the two aqua-ligands stand in opposite position, and there is a 180° angle between them. In the cis-isomer they are in adjacent position, and the angle is 90°. We can see that the two ligands are on the same triangular face of the octahedron, shown in red.
Are there rules that can help us to decide if a cis- or a trans- complex will form? As you might suspect, the largest ligands usually go in trans-position due to steric repulsion arguments. Bidentate ligands usually form the cis-isomer because bidentate ligands are usually designed to make five- or six-membered rings with the metal ion. Are cis-trans isomers chiral? If the ligands are simple, then they are usually not, but if they are more complicated, then they can be. In this context it needs to be said that ideal structures are rarely observed. For example, a square planar complex is rarely an ideal square plane e.g. because the bond angles may be somewhat distorted from the 90° angle due to the fact that the ligands have unequal steric requirements. A slight distortion actually can remove one or many symmetry elements, leading to chirality, however, such small deviations are usually ignored.
Fac-mer Isomerism
Another common type of stereoisomerism in coordination chemistry is fac-mer isomerism. Fac stands for facial and mer stands for meridional. In a fac-isomer the same ligands are on a common face of a polyhedral complex, in the mer isomer they are on a plane that bisects the polyhedron. This kind of isomerism is very common for octahedral complexes, but not restricted to those.

For example the complex triammine trichloro cobalt(III) has a fac- and a mer-isomer. You can see that in the fac-isomer the identical ligands are on two opposite triangular faces of the octahedron. In the mer-isomers they lie on two planes that bisect the octahedron. We can again ask if they are diastereomers or enantiomers? The answer is: They are not mirror images to each other, so they are not enantiomers, but diastereomers.
Fac-mer Isomerism with Tridentate Ligands
Fac-mer isomerism is also common for octahedral complexes with tridentate ligands, for example the ligand diethylenetriamine (Fig. 5.4.15).
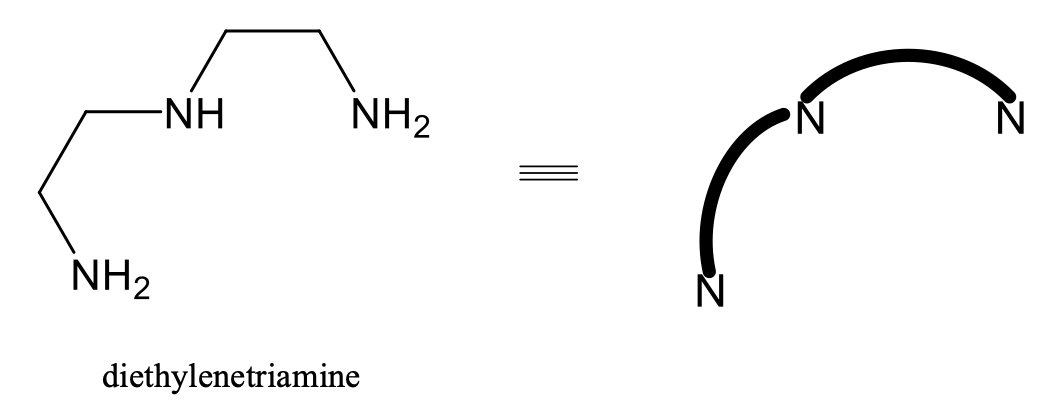
In this ligand two NH2 groups and one NH group are interconnected by two ethylene units. For clarity reasons, in complexes with this ligand, often only the N donor atom of the NH2 and NH groups is depicted, and the ethylene diammine units are simplified as bent lines interconnecting the N-atoms. We will use this simplification in the following (Fig. 5.4.16).
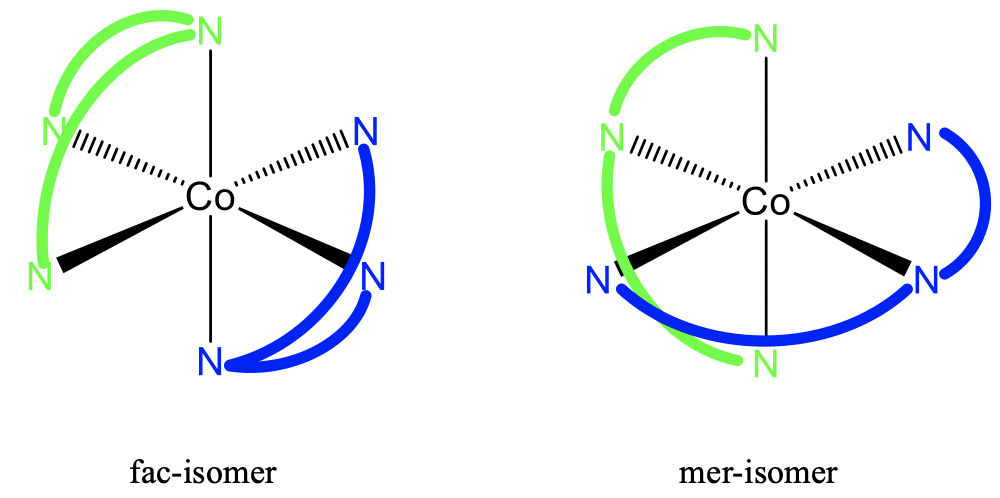
Here is an example of bis(diethylenetriamine) cobalt complexes that are fac-mer isomers (Fig. 5.4.16). One ethylenediamine ligand is shown in green, the other one is shown in blue. You can see that the left isomer is the fac-isomer with all three donor atoms of a ligand placed on the same face of the octahedron. On the right side is the mer-isomer, with all donor atoms of the same ligand placed on planes that bisect the octahedron. Also in this case the two isomers are not mirror images and are diasteromers to each other.
Triethylenetetramine Complexes
There is isomerism similar to fac-mer isomerism in octahedral complexes with the tetradentate ligand triethylenetetramine (Fig. 5.4.17).
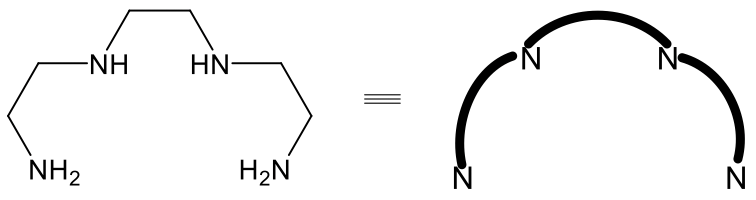
In this ligand, two NH and two NH2 groups are bridged by four ethylene groups. We can again depict the ligand in a simplified way by just showing the N donor atoms, and by simplification of the ethylene groups as bent lines.
One possibility to realize an octahedral complex with triethylenetetraamine ligands is to orient all three rings in the same plane, we can also say we have an octahedral complex with three coplanar rings. This is shown below (Fig.5.4.18).
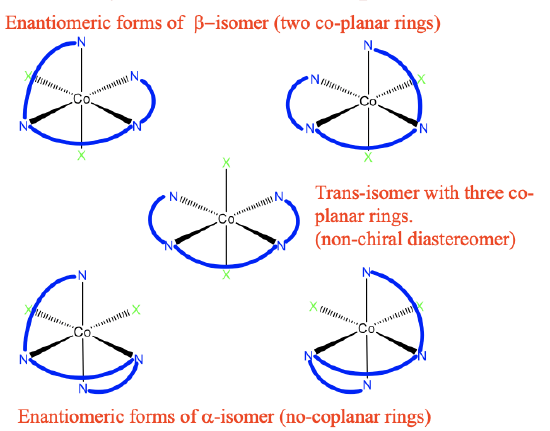
The three ethylenediamine units make three five-membered rings which are co-planar to each other. The N-atoms occupy overall four vertices of the octahedron. There are two other generic ligands X located at to opposite vertices of the octahedron. Therefore, this isomer is called the trans-isomer.
We can ask if this molecule is chiral? The answer is no, because there is a mirror plane which is co-planar with the three five-membered rings. In addition to this trans-isomer, there are also two cis-isomers, one is called the α-isomer, the other one is called the β-isomer. In the β-isomer, there are now only two co-planar rings, the third one is now out of plane. The two ligands X are in cis-position relative to each other. Is the trans-isomer a diastereomer or enantiomer to the β -isomer? They are clearly not mirror images to each other, therefore they must be diasteromers. Is this β-isomer chiral? Yes, it is! There is no improper rotational axis. Therefore, an enantiomer must exist, and this enantiomer must be a mirror image of the β-form. Here it is! Naturally, it must also have two co-planar rings, and two ligands X in cis-position. It is therefore also considered a β-isomer.
Now let us discuss the α-isomerism. In an α-isomer no two ligands are co-planar any more. This isomer is a diasteromer to the trans- and the β-form because the isomers are not mirror images. Also the α-isomer is chiral. Therefore, there must be another α-isomer which is the mirror image to the first α-isomer. It is shown in the bottom right of Figure 5.4.18.
Nomenclature for Propeller Complexes
Complexes with two or more non-coplanar rings that are non-adjacent are always chiral and are called “propeller complexes”. There is a special nomenclature for propeller complexes that we will briefly discuss in the following.
Let us first understand why these complexes are propeller complexes? They are called like that because the non-coplanar rings are oriented relative to each other similarly to propeller blades. A propeller must have at least two blades, but can also have more than that. We distinguish between so-called left handed propellers and right-handed propellers. A left-handed propeller has the property to move away from you in a medium like air or water when rotated counter-clockwise.
Definition: Left-Handed Propeller
Counterclockwise rotation moves a left-handed propeller away
A right handed propeller moves away from you when rotated clock-wise.
Definition: Right-Handed Propeller
Clockwise rotation moves a right-handed propeller away
The tip of one blade of a left-handed propeller describes a left-handed helix as it moves away, the tip of a blade of a right-handed propeller describes are right-handed helix as it moves away.
Determining the Handedness of "Propeller Compexes"
How can we determine the handedness of a propeller molecule? Let us determine it using the example of the tris(oxalato) ferrate(III) anion. Fig. 5.4.19.
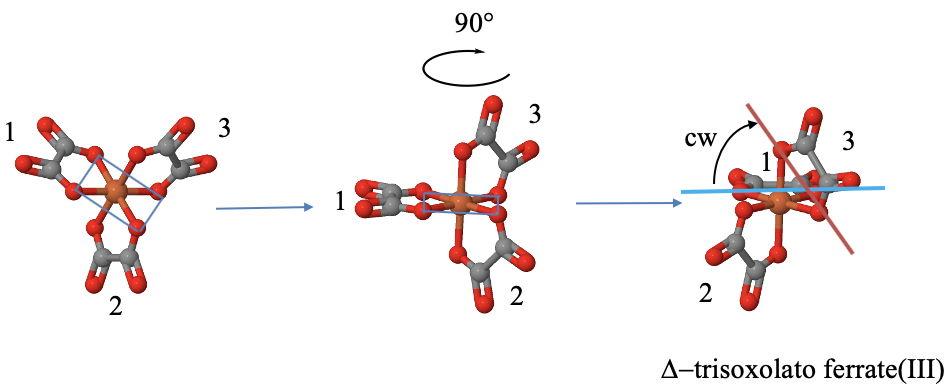
It is a three-bladed propeller molecule because it has three five-membered rings between the three oxolato ligands and the iron center. Each ring is considered a blade. None of the rings are co-planar and none of them are adjacent, meaning that the rings do not share a donor atom.
In order to determine the handedness, we can first rotate the molecule so that one of the rings is oriented horizontally and points to the back. Unless we have a three-dimensional model, we need to do this in our mind. Once that is accomplished we can draw a horizontal line between the two donor atoms of that ring. Next we can draw a line between two donor atoms of another ring. If necessary, we extend the line so that the line crosses the horizontal line. Next, we determine the smallest angle between the two lines, and rotate the non-horizontal line until it becomes horizontal. We can do this just in our mind. If we need to rotate anti-clockwise, the propeller is considered left-handed, we call it a \(\Lambda\) -isomer. If we need to rotate clock-wise, the the propeller is right-handed, we call it \(\Delta\)-isomer.
Determining Handedness for Propeller Molecules Requiring More Than One Label
In some cases coordination compounds have multiple non-adjacent, non-coplanar ring combinations, and the handedness must be determined for each combination. Examples are octahedral EDTA complexes.

In those complexes there are overall five different rings which we can label R1 to R5. You can see the different rings in different colors (Fig. 5.4.20) For clarity we have abbreviated the linkers between the donor atoms by bent lines in different colors. Each color represents a different linker making a different ring.
We realize that ring R3 is shared with all other rings, therefore it is adjacent to all other rings and does not need to be considered. R1 is adjacent to R2, and R3, but not adjacent and not co-planar with R4 and R5. Therefore we need to consider the R1-R4 and R1-R5 combinations. Further, R2 is coplanar with R3 and R4, and adjacent to R3, but is not coplanar and not adjacent to R5. Therefore, we need to consider the R2-R5 combination as well. R4 and R5 are adjacent, so we do not need to consider this combination. We have found all combinations we need.
We now need to rotate the complex so that one relevant ring is oriented horizontally and points to the back. We can for example choose the ring R4. Luckily, is already correctly oriented. Next, we can connect the donor atoms of the ring R4 to produce a horizontal line. Now let us draw a line between the donor atoms of the ring R1. We see that we need to rotate the horizontal line counter-clockwise to make it parallel to this line, thus the R1-R4 ring combination is a \(\Lambda\)-configuration.
We can next determine the R1-R5 handedness by first reorienting the molecule so that R5 points to the back. R1 could also be chosen. However, R5 is part of two relevant ring combinations, and so we can kill two bird with one stone if we choose R5. We can move ring R5 to the back by rotating 90° counter-clockwise around the blue axis shown in Fig. 5.4.20. In goes through an O atom, the cobalt atom, and an N atom. This axis stands perpendicular to the square indicated by dotted lines. The square has four donor atoms on the four vertices, and these donor atoms move 90° counter-clockwise as the rotation is carried out. The orientation of the rings follow the movement of the donor atoms. The O-donor atom of the ring R5 moves so that R5 is now horizontal, and points to the back. Next we can interconnect the donor atoms of R5, and the donor atoms of R1 by lines. We can see that the horizontal line must be rotated clockwise so that it becomes parallel with the other one. Therefore, the R1-R5 configuration is a \(\Delta\)-configuration.
For the determination of the combination R2-R5 the complex does not need to be reoriented again. We can directly draw a line through the donor atoms of R2, and determine the direction of rotation. This time we need to rotate counter-clockwise again, meaning the R2-R5 combination is in \(\Lambda\)-configuration.
Overall, we have a ΛΔΛ-(ethylenediamine tetracetato)cobaltate(III). Note that the order of designation is arbitrary, we could have named the molecule a ΛΛΔ-complex or a ΔΛΛ-complex also.
Exercise
Let us practice this by one more example.
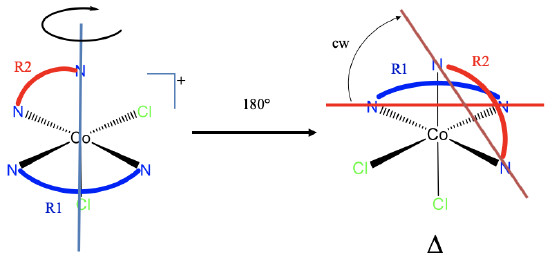
What is the handedness of the complex shown? First of all: Does it meet the criteria for a propeller complex? The answer is yes. There are two rings, R1 and R2, and they are both not coplanar, and non-adjacent.
To determine handedness we need to first move the molecule so that one ring is oriented horizontally and points to the back. We could choose any of them, but it seems easier to rotate the ring R1 that points to the front and is oriented horizontally by 180° around an axis that is defined by one N and on Cl atom (shown in blue in Fig. 5.4.21)), and is oriented vertically. This rotation moves one of the donor atoms of the other ring by 180°, which defines the new orientation of the ring. Now we can draw a horizontal line through the donor atom of ring 1, and a line through the donor atoms of ring R2. We can see that we must rotate clock-wise, and the propeller complex is right-handed.
Ring Conformations
In addition to isomerism, also conformerism has an influence on the structure of a coordination compound. There may be two or more conformers possible for a particular isomer. As an example, let us consider a ring between a metal ion and an ethylenediamine ligand (Fig. 5.4.22).
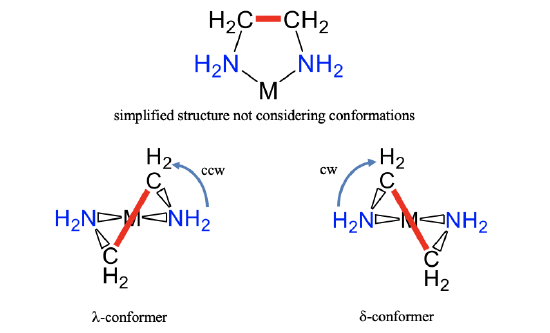
In contrast to simplified depictions often used, it is not planar, because of the sp3-hybridization of the carbon and nitrogen atoms. There are two different conformations possible that differ in the orientation of the C-C bond within the ring. They are shown above (Fig. 5.4.22). In the conformation shown left we must rotate a thought horizontal line going through the two nitrogen donor atoms counterclockwise so that it becomes parallel to the C-C bond. For the other conformer, we need to rotate the thought horizontal line clockwise. We call the first conformer the \(\lambda\)-conformer, and the second one the \(\delta\)-conformer. In this case we use lower case letters to indicate conformerism and not isomerism.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


