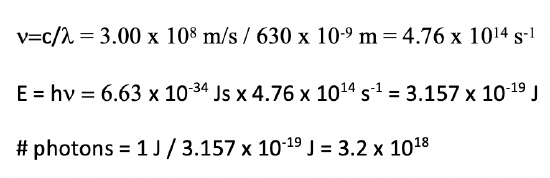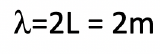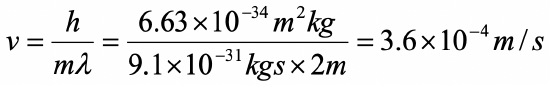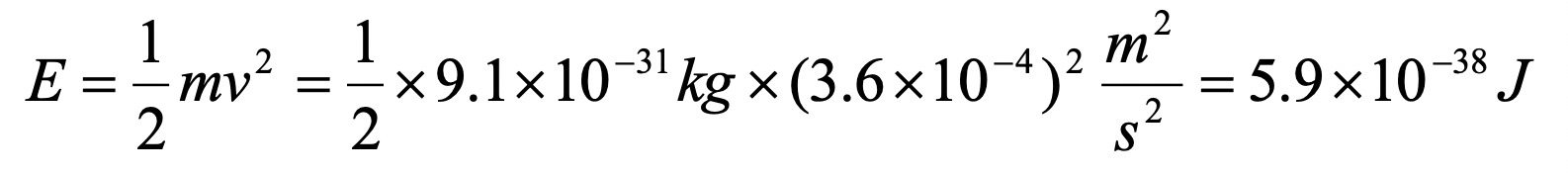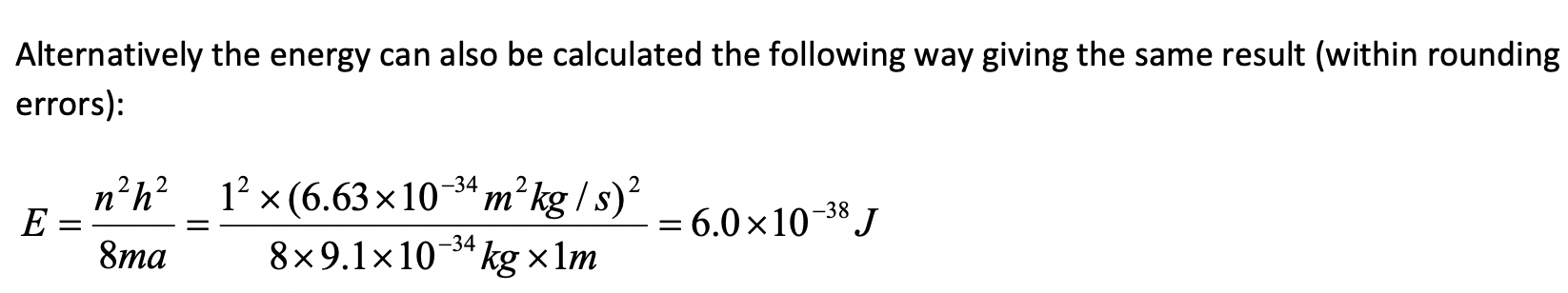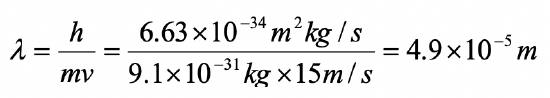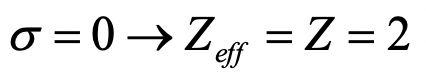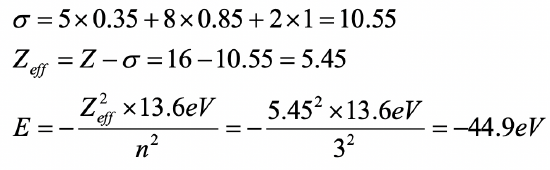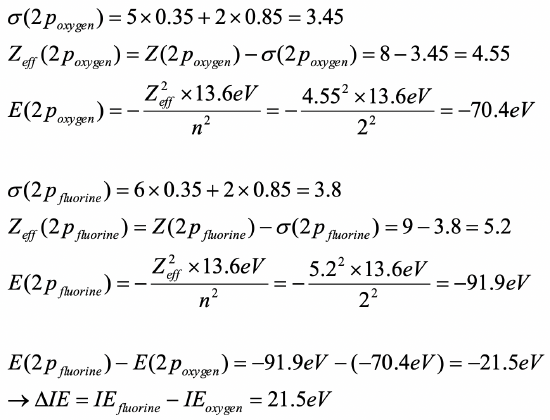Section 1
Exercise 1
Cobalt forms two sulfides, CoS and Co2 S3. Predict the ratio of the masses of sulfur that combine with a fixed mass of cobalt to form CoS and Co2S3
- Answer
-
In Co2S3 there are 1.5 S atoms per Co atom
In CoS there is 1 S atom per Co atom
Mass ratio of S in the two compounds is 1:1.5 = 2:3
Exercise 2
What is true about the Rutherford atom model?
- It explains why atoms do not send out electromagnetic radiation permanently
- It explains why alpha particles get scattered by atoms
- It explains the atomic spectrum of the hydrogen atom
- It explains the wave-particle dualism
- Answer
-
b) It explains why alpha particles get scattered by atoms
Exercise 3
The Bohr radius (the radius of the electron orbit for the H atom in its ground state) is 5.29 x 10-11 m. Calculate the radius of an electron in the third shell of the H atom according to the Bohr atom model.
- Answer
-
r3 = 32 x 5.29 x 10-11 m = 47.61 x 10-11 m.
Section 2
Exercise 1
The electron in an H atom undergoes an electronic transition from the 3rd to the 2nd shell. What frequency does the light that is emitted have? The energy of the electron in the first shell is -2.18 x 10-18 J.
- Answer
-
Energy of electron in the 3rd shell: E3 = -2.18 x 10-18 J / 32 = -0.24 x 10-18 J
Energy of electron in the 2nd shell: E2 = -2.18 x 10-18 J / 22 = -0.545 x 10-18 J
Energy difference between the two electrons: E3-E2 = 0.305 x 10-18 J
Frequency of emitted light: n=(E3-E2)/h = 0.305 x 10-18 J/ 6.63 x 10-34 Js = 4.60 x 1014 s-
Exercise 2
What is the mass of a photon with a wavelength of 400 nm that travels though space?
- Answer
-
λ = h/mc --> m = h/λc = 6.63 x 10-34Js / (400 x 10-9 m x 3.00 x 108 m/s) = 5.525 x 10-36 kg.
Exercise 3
Two objects are moving at the same speed. Which (if any) of the following statements are true?
- The DeBroglie wavelength of the heavier object is longer than that of the lighter one.
- If one object has twice as much mass as the other, its wavelength is one-half of the other
- Doubling the speed of one of the objects will have the same effect on its wavelength as doubling its mass.
- Answer
-
a) If one object has twice as much mass as the other, its wavelength is one-half of the other
b) Doubling the speed of one of the objects will have the same effect on its wavelength as doubling its mass
Exercise 4
The power of a red laser with a wavelength of 630 nm) is 1.00 Watt (1.00 Js). How many photons per second does the laser emit?
- Answer
-
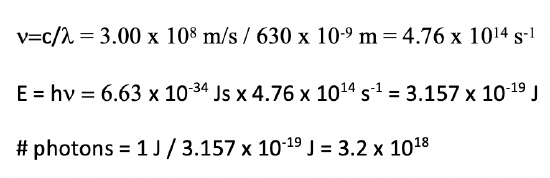
Exercise 5
Which of the following waves would you consider to be standing matter wave?
- The vibration of a drum.
- Sound traveling through open air.
- A tsunami.
- None of the above.
- Answer
-
a) The vibration of a drum.
Exercise 6
Assume an electron travels in a one-dimensional box (as discussed in class) of the length of 1 m. Look up relevant constants in the internet or a suitable textbook.
- What is the wavelength of the associated standing matter wave in the ground state?
- What is the velocity of the electron in the ground state?
- What is the energy of the electron in the ground state?
- Answer
-
a) 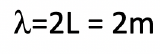
b) 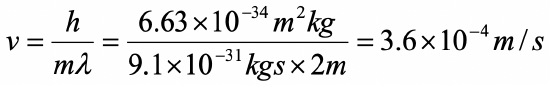
c) 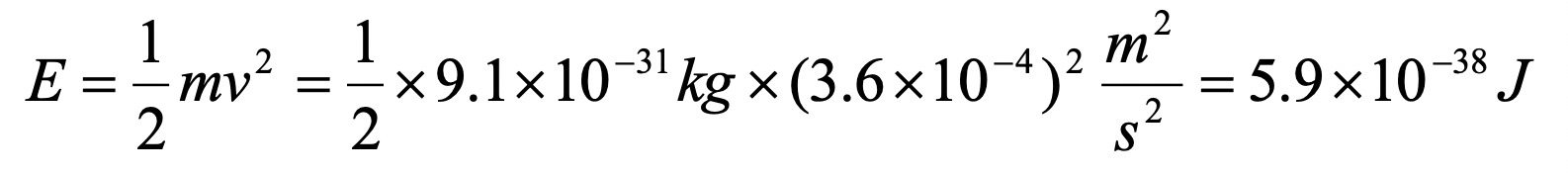
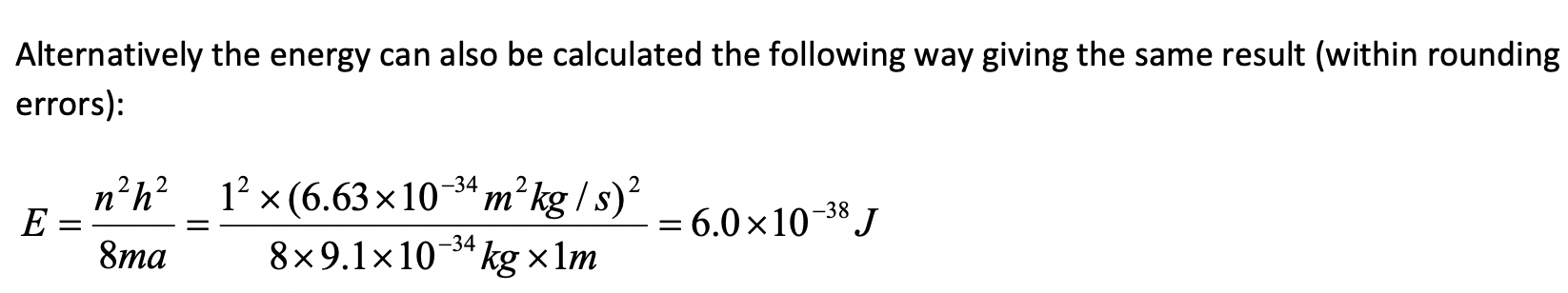
Exercise 7
An electron in the first excited state travels with a velocity of 15 m/s within a one-dimensional box. What is the length of the box?
- Answer
-
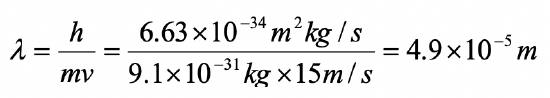
In the first excited state n =2. For n = the length of the box is equal to the wavelength. Therefore the length of the box is 4.9 x 10-5 m.
Exercise 8
What are orbitals (more than one answer can be correct)?
- Wave functions that describe the electrons as three-dimensional standing matter waves in an atom.
- Spaces inside an atom in which the electron travels as a classical particle.
- Solutions of the Schrödinger equation for the hydrogen atom.
- Answer
-
a) Wave functions that describe the electrons as three-dimensional standing matter waves in an atom.
c) Solutions of the Schrödinger equation for the hydrogen atom.
Exercise 9
Which quantum numbers l are allowed when the quantum number n is 4?
- Answer
-
l can be 3,2,1,0
Exercise 10
Which quantum numbers m are allowed when the quantum number l is 3?
- Answer
-
-3,-2,-1,0,+1,+2,+3
Exercise 11
What is true about the following wave function?
\[\Psi=\frac{1}{\sqrt{2 \pi}} \quad \frac{\sqrt{6}}{2} \cos \theta \quad \frac{4}{81 \sqrt{6} a_0 3 / 2}\left[6-\frac{r}{a_0}\right] \frac{r}{a_0} e^{-r / 3 a_0} \nonumber\]
- Its does not have angular nodes
- Its does not have spherical nodes
- Its amplitude is 0 at the nucleus
- The wave function represents an s orbital
- Answer
-
c) Its amplitude is 0 at the nucleus
Exercise 12
The angular part of the wavefunction of an orbital has the following form:
\[\Theta \Phi(x, y, z)=\frac{1}{4} \sqrt{\frac{15}{\pi}} \frac{\left(x^2-y^2\right)}{r^2} \nonumber\]
Which planes are the planar nodes in this orbital?
- Answer
-
The wavefunction is 0 for x=y and x=-y. So it is two planes that bisect the x and the y axis.
Exercise 13
Order the following orbitals with respect to their penetration abilities:
4s, 4p, 4d, 4f
- Answer
-
4s > 4p > 4d > 4f
Exercise 14
What is the effective nuclear charge on an electron in an He+ ion?
- Answer
-
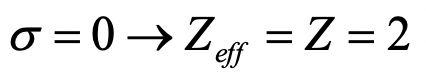
Exercise 15
Calculate the orbital energy of a 3p electron in a sulfur atom using the Slater rules.
- Answer
-
(1s2) (2s2 2p6) (3s2 3p4)
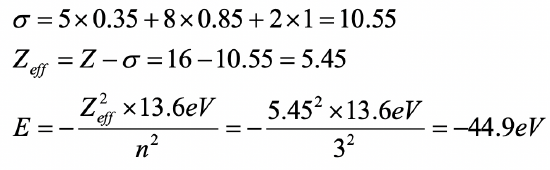
Exercise 16
Calculate the orbital energy of a 3d electron in a palladium atom using the Slater rules.
- Answer
-
(1s2) (2s2 2p6) (3s2 3p6)(3d10)(4s24p6)(4d8)(5s2)

Exercise 17
Calculate how much higher the first ionization energy of an oxygen atom is compared to a fluorine atom. Use the Slater rules to answer the question.
- Answer
-
O: (1s2 ) (2s2 2p4)
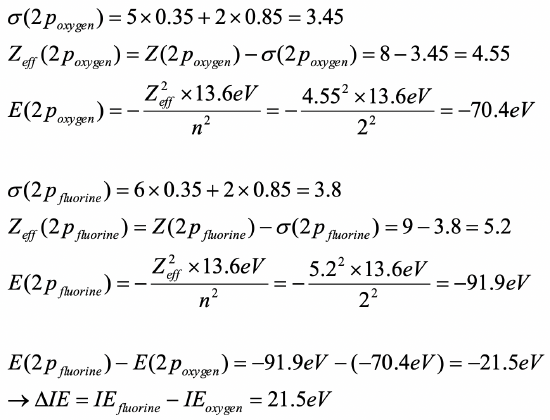
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.