2.5: Isotopes and Atomic Mass
- Last updated
- Save as PDF
- Page ID
- 208939
Learning Outcomes
- Define atomic and mass numbers.
- Determine the number of protons, neutrons, and electrons in an atom.
- Identify the charge and relative mass of subatomic particles.
- Label the location of subatomic particles in the atom.
- Define isotope.
- Write the isotopic symbol of an atom.
- Explain the concept of average atomic mass.
Atoms are the fundamental building blocks of all matter and are composed of protons, neutrons, and electrons. Because atoms are electrically neutral, the number of positively charged protons must be equal to the number of negatively charged electrons. Since neutrons do not affect the charge, the number of neutrons is not dependent on the number of protons and will vary even among atoms of the same element.
Atomic Number
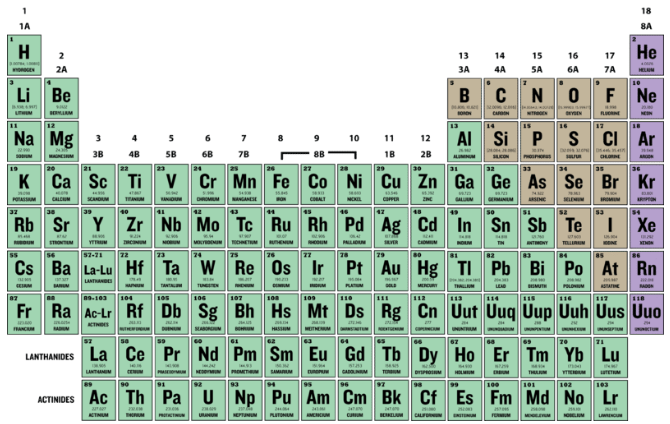
The atomic number (Z) of an element is the number of protons in the nucleus of each atom of that element. An atom can be classified as a particular element based solely on its atomic number. For example, any atom with an atomic number of 8 (its nucleus contains 8 protons) is an oxygen atom, and any atom with a different number of protons would be a different element. The periodic table (see figure below) displays all of the known elements and is arranged in order of increasing atomic number. In this table, an element's atomic number is indicated above the elemental symbol. Hydrogen, at the upper left of the table, has an atomic number of 1. Every hydrogen atom has one proton in its nucleus. Next on the table is helium, whose atoms have two protons in the nucleus. Lithium atoms have three protons, beryllium atoms have four, and so on.
Since atoms are neutral, the number of electrons in an atom is equal to the number of protons. Hydrogen atoms all have one electron occupying the space outside of the nucleus. Helium, with two protons, will have two electrons.
Mass Number
Experimental data showed that the vast majority of the mass of an atom is concentrated in its nucleus, which is composed of protons and neutrons. The mass number is defined as the total number of protons and neutrons in an atom. Consider the table below, which shows data from the first six elements of the periodic table.
| Name | Symbol | Atomic Number | Protons | Neutrons | Electrons | Mass Number |
|---|---|---|---|---|---|---|
| hydrogen | \(\ce{H}\) | 1 | 1 | 0 | 1 | 1 |
| helium | \(\ce{He}\) | 2 | 2 | 2 | 2 | 4 |
| lithium | \(\ce{Li}\) | 3 | 3 | 4 | 3 | 7 |
| beryllium | \(\ce{Be}\) | 4 | 4 | 5 | 4 | 9 |
| boron | \(\ce{B}\) | 5 | 5 | 6 | 5 | 11 |
| carbon | \(\ce{C}\) | 6 | 6 | 6 | 6 | 12 |
View animations showing the atomic structure of the first 11 elements on the periodic table at http://web.visionlearning.com/custom...imations.shtml
Consider the element helium. Its atomic number is 2, so it has two protons in its nucleus. Its nucleus also contains two neutrons. Since \(2 + 2 = 4\), we know that the mass number of the helium atom is 4. Finally, the helium atom also contains two electrons, since the number of electrons must equal the number of protons. This example may lead you to believe that atoms have the same number of protons and neutrons, but a further examination of the table above will show that this is not the case. Lithium, for example, has three protons and four neutrons, giving it a mass number of 7.
Knowing the mass number and the atomic number of an atom allows you to determine the number of neutrons present in that atom by subtraction.
\[\text{Number of neutrons} = \text{mass number} - \text{atomic number}\]
Atoms of the element chromium \(\left( \ce{Cr} \right)\) have an atomic number of 24 and a mass number of 52. How many neutrons are in the nucleus of a chromium atom? To determine this, you would subtract as shown:
\[52 - 24 = 28 \: \text{neutrons in a chromium atom}\]
The composition of any atom can be illustrated with a shorthand notation using the atomic number and the mass number. Both are written before the chemical symbol, with the mass number written as a superscript and the atomic number written as a subscript. The chromium atom discussed above would be written as:
\[\ce{^{52}_{24}Cr}\]
Another way to refer to a specific atom is to write the mass number of the atom after the name, separated by a hyphen. The above atom would be written as chromium-52, with the mass number written after the name. The atomic number does not have to be included because all atoms of chromium have the same number of protons but can vary in the atomic mass.
Isotopes
As stated earlier, not all atoms of a given element are identical. Specifically, the number of neutrons in the nucleus can vary for many elements. As an example, naturally occurring carbon exists in three forms, which are illustrated in the figure below.

Each carbon atom has the same number of protons (6), which is equal to its atomic number. Each carbon atom also contains six electrons, allowing the atom to remain electrically neutral. However, the number of neutrons varies from six to eight. Isotopes are atoms that have the same atomic number but different mass numbers due to a change in the number of neutrons. The three isotopes of carbon can be referred to as carbon-12 \(\left( \ce{^{12}_6C} \right)\), carbon-13 \(\left( \ce{^{13}_6C} \right)\), and carbon-14 \(\left( \ce{^{14}_6C} \right)\). Naturally occurring samples of most elements are mixtures of isotopes. Carbon has only three natural isotopes, but some heavier elements have many more. Tin has ten stable isotopes, which is the most of any known element. The nucleus of a given carbon atom will be one of the three possible isotopes discussed above.
While the presence of isotopes affects the mass of an atom, it does not affect its chemical reactivity. Chemical behavior is governed by the number of electrons and the number of protons. Carbon-13 behaves chemically in exactly the same way as the more plentiful carbon-12.
Size of Atoms
The graphite in your pencil is composed of the element carbon, a nonmetal. Imagine taking a small piece of carbon and grinding it until it is a fine dust. Each speck of carbon would still have all of the physical and chemical properties of carbon. Now imagine that you could somehow keep dividing the speck of carbon into smaller and smaller pieces. Eventually, you would reach a point where your carbon sample is as small as it could possibly be. This final particle is called an atom.
Atoms, as you probably know, are extremely small. In fact, the graphite in an ordinary pencil contains about \(5 \times 10^{20}\) atoms of carbon. This is an almost incomprehensibly large number. The population of the entire Earth is about \(7 \times 10^9\) people, meaning that there are about \(7 \times 10^{10}\) times as many carbon atoms in your pencil as there are people on Earth! For this to be true, atoms must be extremely small. We can only see atoms with a modern instrument called a scanning tunneling microscope. (www.nobelprize.org/educationa...opes/scanning/)
Atomic Mass
The masses of individual atoms are very, very small. However, using a modern device called a mass spectrometer, it is possible to measure such miniscule masses. An atom of oxygen-16, for example, has a mass of \(2.66 \times 10^{-23} \: \text{g}\). While comparisons of masses measured in grams would have some usefulness, it is far more practical to have a system that will allow us to more easily compare relative atomic masses. Scientists decided on using the carbon-12 nuclide as the reference standard by which all other masses would be compared. By definition, one atom of carbon-12 is assigned a mass of exactly 12 atomic mass units \(\left( \text{amu} \right)\). An atomic mass unit is defined as a mass equal to one twelfth of an atom of carbon-12. The mass of any isotope of any element is expressed in relation to the carbon-12 standard. For example, one atom of helium-4 has a mass of \(4.0026 \: \text{amu}\). An atom of sulfur-32 has a mass of \(31.972 \: \text{amu}\).
The carbon-12 atom has six protons and six neutrons in its nucleus for a mass number of 12. Since the nucleus accounts for nearly all of the mass of the atom, a single proton or single neutron has a mass of approximately \(1 \: \text{amu}\). However, as seen by the helium and sulfur examples, the masses of individual atoms are not quite whole numbers. This is because an atom's mass is affected very slightly by the interactions of the various particles within the nucleus and also includes the small mass added by each electron.
As stated in the section on isotopes, most elements occur naturally as a mixture of two or more isotopes. Listed below (see table below) are the naturally occurring isotopes of several elements along with the percent natural abundance of each.
| Element | Isotope (Symbol) | Percent Natural Abundance | Atomic mass \(\left( \text{amu} \right)\) | Average atomic mass \(\left( \text{amu} \right)\) |
|---|---|---|---|---|
| Hydrogen | \(\ce{^1_1H}\) | 99.985 | 1.0078 | 1.0079 |
| \(\ce{^2_1H}\) | 0.015 | 2.0141 | ||
| \(\ce{^3_1H}\) | negligible | 3.0160 | ||
| Carbon | \(\ce{^{12}_6C}\) | 98.89 | 12.000 | 12.011 |
| \(\ce{^{13}_6C}\) | 1.11 | 13.003 | ||
| \(\ce{^{14}_6C}\) | trace | 14.003 | ||
| Oxygen | \(\ce{^{16}_8O}\) | 99.759 | 15.995 | 15.999 |
| \(\ce{^{17}_8O}\) | 0.037 | 16.995 | ||
| \(\ce{^{18}_8O}\) | 0.204 | 17.999 | ||
| Chlorine | \(\ce{^{35}_{17}Cl}\) | 75.77 | 34.969 | 35.453 |
| \(\ce{^{37}_{17}Cl}\) | 24.23 | 36.966 | ||
| Copper | \(\ce{^{63}_{29}Cu}\) | 69.17 | 62.930 | 63.546 |
| \(\ce{^{65}_{29}Cu}\) | 30.83 | 64.928 |
For some elements, one particular isotope is much more abundant than any other isotopes. For example, naturally occurring hydrogen is nearly all hydrogen-1, and naturally occurring oxygen is nearly all oxygen-16. For many other elements, however, more than one isotope may exist in substantial quantities. Chlorine (atomic number 17) is yellowish-green toxic gas. About three quarters of all chlorine atoms have 18 neutrons, giving those atoms a mass number of 35. About one quarter of all chlorine atoms have 20 neutrons, giving those atoms a mass number of 37. Were you to simply calculate the arithmetic average of the precise atomic masses, you would get approximately 36.
\[\frac{34.969 + 36.966}{2} = 35.968\]
As you can see, the average atomic mass given in the last column of the table above is significantly lower. Why? The reason is that we need to take into account the natural abundance percentages of each isotope in order to calculate what is called the weighted average. The atomic mass of an element is the weighted average of the atomic masses of the naturally occurring isotopes of that element. The average atomic masses are the values we see on the periodic table.
\[0.7577 \left( 34.969 \right) + 0.2423 \left( 36.966 \right) = 35.453\]
The weighted average is determined by multiplying the percent of natural abundance by the actual mass of the isotope. This is repeated until there is a term for each isotope. For chlorine, there are only two naturally occurring isotopes so there are only two terms.
Supplemental Resources
- Elements and Atoms: http://www.youtube.com/watch?v=IFKnq9QM6_A
- Introduction to the Atom: http://www.youtube.com/watch?v=1xSQIwWGT8M
- Atomic History - A Brief Discovery: http://www.pbs.org/wgbh/nova/diamond...dehistory.html
- All About Atoms: http://education.jlab.org/atomtour/index.html
- Build and Atom: http://phet.colorado.edu/en/simulation/build-an-atom
- Molecular Workbench - Atomic Structure: http://workbench.concord.org/databas...vities/47.html
- See Inside a Diamond: http://www.pbs.org/wgbh/nova/diamond/insidewave.html
- Isotopes and Atomic Mass: http://phet.colorado.edu/en/simulati...nd-atomic-mass
- Atomic Structure: freezeray.com/flashFiles/atomcStructure.htm
- Atom Builder: freezeray.com/flashFiles/atomBuilder.htm
- Tennis Ball Isotopes: http://www.youtube.com/watch?v=oLnuXpf4hsA
- Element Math Game: http://education.jlab.org/elementmath/index.html
- Atoms and Matter Crossword Puzzle: http://education.jlab.org/sciencecro.../atoms_01.html
- Atomic Number Review #1: www.sciencegeek.net/Chemistry...micNumbers.htm
- Atomic Number Review #2: www.sciencegeek.net/Chemistry...t1Numbers2.htm
- Atomic Structure: www.sciencegeek.net/Chemistry...omicStructure/
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)


