6.1: Nuclear Magnetic Resonance Spectroscopy
- Page ID
- 227578
Objectives
After completing this section, you should be able to
- discuss the principles of NMR spectroscopy.
- identify the two magnetic nuclei that are most important to an organic chemist.
Key Terms
Make certain that you can define, and use in context, the key term below.
- resonance
Study Notes
Notice that the word “resonance” has a different meaning when we are discussing nuclear magnetic resonance spectroscopy than it does when discussing molecular structures.
Introduction
Some types of atomic nuclei act as though they spin on their axis similar to the Earth. Since they are positively charged they generate an electromagnetic field just as the Earth does. So, in effect, they will act as tiny bar magnetics. Not all nuclei act this way, but fortunately both 1H and 13C do have nuclear spins and will respond to this technique.

NMR Spectrometer
In the absence of an external magnetic field the direction of the spin of the nuclei will be randomly oriented (see figure below left). However, when a sample of these nuclei is place in an external magnetic field, the nuclear spins will adopt specific orientations much as a compass needle responses to the Earth’s magnetic field and aligns with it. Two possible orientations are possible, with the external field (i.e. parallel to and in the same direction as the external field) or against the field (i.e. antiparallel to the external field). Nuclei in line with the magnetic field have a slightly lower energy than those aligned against the magnetic field (��E). The difference in energy depends on the. intensity of the applied magnetic field Bo.
See figure below right.
Figure 1: (Left) Random nuclear spin without an external magnetic field. (Right)Ordered nuclear spin in an external magnetic field
If the ordered nuclei are now subjected to EM radiation of the proper frequency the nuclei aligned with the field will absorb energy and "spin-flip" to align themselves against the field, a higher energy state. When this spin-flip occurs the nuclei are said to be in "resonance" with the field, hence the name for the technique, Nuclear Magentic Resonance or NMR.
The amount of energy, and hence the exact frequency of EM radiation required for resonance to occur is dependent on both the strength of the magnetic field applied and the type of the nuclei being studied, but it is always located in the radio wave region of the electromagnetic spectrum. As the strength of the magnetic field increases the energy difference between the two spin states increases and a higher frequency (more energy) EM radiation needs to be applied to achieve a spin-flip (see image below).
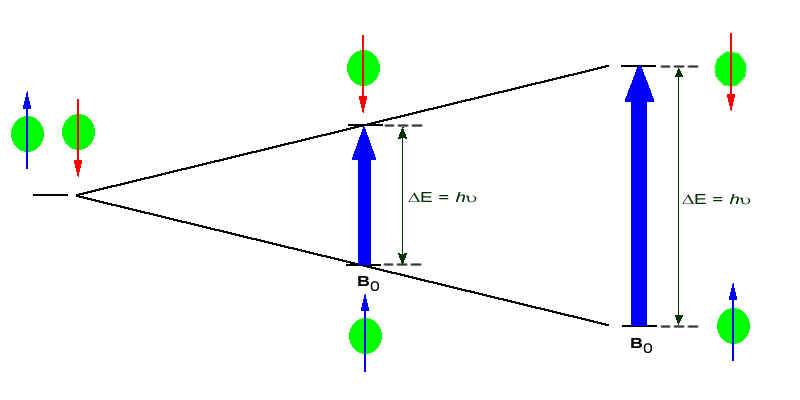
Superconducting magnets can be used to produce very strong magnetic field, on the order of 21 tesla (T). Lower field strengths can also be used, in the range of 4 - 7 T. At these levels the energy required to bring the nuclei into resonance is in the MHz range and corresponds to radio wavelength energies, i.e. at a field strength of 4.7 T 200 MHz bring 1H nuclei into resonance and 50 MHz bring 13C into resonance. This is considerably less energy then is required for IR spectroscopy, ~10-4 kJ/mol versus ~5 - ~50 kJ/mol.
1H and 13C are not unique in their ability to undergo NMR. All nuclei with an odd number of protons (1H, 2H, 14N, 19F, 31P ...) or nuclei with an odd number of neutrons (i.e. 13C) show the magnetic properties required for NMR. Only nuclei with even number of both protons and neutrons (12C and 16O) do not have the required magnetic properties.
Exercise
13.1 Nuclear Magnetic Resonance Spectroscopy
13.1 Exercises
Questions
Q13.1.1
If in a field strength of 4.7 T, H1 requires 200 MHz of energy to maintain resonance. If atom X requires 150 MHz, calculate the amount of energy required to spin flip atom X’s nucleus. Is this amount greater than the energy required for hydrogen?
Q13.1.2
Calculate the energy required to spin flip at 400 MHz. Does changing the frequency to 500 MHz decrease or increase the energy required? What about 300 MHz.
Solutions
S13.1.1
E = hυ
E = (6.62 × 10−34)(150 MHz)
E = 9.93 × 10−26 J
The energy is equal to 9.93x10-26 J. This value is smaller than the energy required for hydrogen (1.324 × 10−25 J).
S13.1.2
E = hυ
E = (6.62 × 10−34)(400 MHz)
E = 2.648 × 10−25 J
The energy would increase if the frequency would increase to 500 MHz, and decrease if the frequency would decrease to 300 MHz.
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)

