Homework 4

Last updated
Save as PDF

Page ID: 204077

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Q1

Answer True/False for the following questions regarding Hückel Theory. If false, explain why.

Only p electrons are considered
Each molecular orbital is made up of a linear combination of atomic orbitals
The overlap integrals for orbitals on adjacent atoms are given the value \(\beta\).
All Coulomb integrals (\(H_{ii}\) are given the value \(\alpha\)
The Coulomb integral, \(\alpha\), and the resonance integral, \(\beta\), are positive energy quantities.
The value of the resonance integral for adjacent carbon atoms is zero.
The value of the resonance integral for non-adjacent carbon atoms is \(\beta\).
In finding the molecular orbitals, the secular determinant must be zero for a non-trivial solution.

Q2

Derive Equation 10.5.11 from the Schrödinger equation and LCAO approximation for ethylene.

Q3

Consider the cyclopentadienyl radical anion with \( | i \rangle \) representing the \(|p_z \rangle \) on the n^th carbon

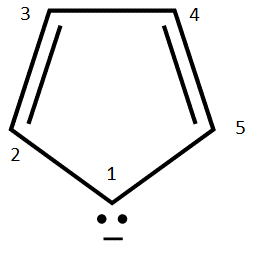
=aromatic7.png

Considering the five \(\pi\) wavefunctions constructed within the Hückel approximation:

\( | \pi_1 \rangle = +0.45 | 1 \rangle +0.45 | 2 \rangle + +0.45 | 3 \rangle +0.45 | 4 \rangle +0.45 |5 \rangle \)
\( | \pi_2 \rangle = -0.51 | 1 \rangle + 0.63 | 2 \rangle -0.51 | 3 \rangle + 0.20 | 4 \rangle + 0.20 | 5 \rangle \)
\( | \pi_3 \rangle = -0.37 | 1 \rangle + 0.37 | 3 \rangle + 0.60 | 4 \rangle + 0.60 | 5 \rangle \)
\( | \pi_4 \rangle = -0.21 | 1 \rangle - 0.63 | 2 \rangle -0.20 | 3 \rangle + 0.51 | 4 \rangle + 0.51 | 5 \rangle \)
\( | \pi_5 \rangle = +.6 | 1 \rangle -0.60 | 3 \rangle + 0.37 | 4 \rangle + 0.37 | 5 \rangle \)

Write down the matrix form for the Hamiltonian in a basis set of p orbitals on each carbon (1–5 above) within the Hückel approximation. Use the usual a and b abbreviations for the integrals in the problem.
Choose one of the wavefunctions and show that is normalized (within ± 0.1).
Choose two of the wavefunctions and show that they are orthogonal (within ± 0.1).
Use the matrix written down in part (a) to calculate the unique three energies using these eigenfunctions

Q4

The allyl cation \(CH_2=CH-CH^+\) has a delocalized \(\pi\) network that can be described by Huckel method. Derive the MO energy levels for this species and place the electrons in the levels appropriate for the ground state. Using the butadiene MO’s as an example, sketch what you would expect the \(\pi\) MOs to look like. Classify each orbital as bonding, antibonding or nonbonding. What is the delocalization energy for the allyl cation (compare to the 1.5 times the ethylene total energy)?