8.E: Gravimetric Methods (Exercises)
- Page ID
- 198754
1. Starting with the equilibrium constant expressions for reaction 8.1, and reactions 8.3–8.5, verify that equation 8.7 is correct.
2. Equation 8.7 explains how the solubility of AgCl varies as a function of the equilibrium concentration of Cl–. Derive a similar equation that describes the solubility of AgCl as a function of the equilibrium concentration of Ag+. Graph the resulting solubility function and compare it to that shown in Figure 8.1.
3. Construct a solubility diagram for Zn(OH)2 that takes into account the following soluble zinc-hydroxide complexes: Zn(OH)+, Zn(OH)3–, and Zn(OH)42–. What is the optimum pH for quantitatively precipitating Zn(OH)2? For your solubility diagram, plot log(S) on the y-axis and pH on the x-axis. See the appendices for relevant equilibrium constants.
4. Starting with equation 8.10, verify that equation 8.11 is correct.
5. For each of the following precipitates, use a ladder diagram to identify the pH range where the precipitates has its lowest solubility? See the appendices for relevant equilibrium constants.
a. CaC2O4 b. PbCrO4 c. BaSO4 d. SrCO3 e. ZnS
6. Mixing solutions of 1.5 M KNO3 and 1.5 M HClO4 produces a white precipitate of KClO4. If permanganate ions are present, an inclusion of KMnO4 is possible. Impure precipitates of KClO4 are purple if an inclusion of KMnO4 is present. Shown below are descriptions of two experiments in which KClO4 is precipitated in the presence of MnO4–. Explain why the experiments lead to the different results shown in Figure 8.15.
Experiment 1. Place 1 mL of 1.5 M KNO3 in a test tube, add 3 drops of 0.1 M KMnO4, and swirl to mix. Add 1 mL of 1.5 M HClO4 dropwise, agitating the solution between drops. Destroy the excess KMnO4 by adding 0.1 M NaHSO3 dropwise. The resulting precipitate of KClO4 has an intense purple color.
Experiment 2. Place 1 mL of 1.5 M HClO4 in a test tube, add 3 drops of 0.1 M KMnO4, and swirl to mix. Add 1 mL of 1.5 M KNO3 dropwise, agitating the solution between drops. Destroy the excess KMnO4 by adding 0.1 M NaHSO3 dropwise. The resulting precipitate of KClO4 has a pale purple in color.

Figure 8.15 Results for the experiments in Problem 8.6. (a) Experiment 1; (b) Experiment 2.
7. Mixing solutions of Ba(SCN)2 and MgSO4 produces a precipitate of BaSO4. Shown below are the descriptions and results for three experiments using different concentrations of Ba(SCN)2 and MgSO4. Explain why these experiments produce different results.
Experiment 1. When equal volumes of 3.5 M Ba(SCN)2 and 3.5 M MgSO4 are mixed, a gelatinous precipitate immediately forms.
Experiment 2. When equal volumes of 1.5 M Ba(SCN)2 and 1.5 M MgSO4 are mixed, a curdy precipitate immediately forms. Individual particles of BaSO4 can be seen as points under a magnification of 1500×(a particle size less than 0.2 μm).
Experiment 3. When equal volumes of 0.5 mM Ba(SCN)2 and 0.5 mM MgSO4 are mixed, the complete precipitation of BaSO4 requires 2–3 h. Individual crystals of BaSO4 obtain lengths of approximately 5 μm.
8. Aluminum is determined gravimetrically by precipitating Al(OH)3 and isolating Al2O3. A sample containing approximately 0.1 grams of Al is dissolved in 200 mL of H2O, and 5 grams of NH4Cl and a few drops of methyl red indicator are added (methyl red is red at pH levels below 4 and yellow at pH levels above 6). The solution is heated to boiling and 1:1 NH3 is added dropwise till the indicator turns yellow, precipitating Al(OH)3. The precipitate is held at the solution’s boiling point for several minutes before filtering and rinsing with a hot solution of 2% w/v NH4NO3. The precipitate is then ignited at 1000–1100oC, forming Al2O3.
(a) Cite two ways in which this procedure encourages the formation of larger particles of precipitate.
(b) The ignition step must be carried out carefully to ensure the quantitative conversion of Al(OH)3 to Al2O3. What is the effect of an incomplete conversion on the %w/w Al?
(c) What is the purpose of adding NH4Cl and methyl red indicator?
(d) An alternative procedure involves isolating and weighing the precipitate as the 8-hydroxyquinolate, Al(C9H6ON)3. Why might this be a more advantageous form of Al for a gravimetric analysis? Are there any disadvantages?
9. Calcium is determined gravimetrically by precipitating CaC2O4•H2O and isolating CaCO3. After dissolving a sample in 10 mL of water and 15 mL of 6 M HCl, the resulting solution is heated to boiling and a warm solution of excess ammonium oxalate is added. The solution is maintained at 80oC and 6 M NH3 is added dropwise, with stirring, until the solution is faintly alkaline. The resulting precipitate and solution are removed from the heat and allowed to stand for at least one hour. After testing the solution for completeness of precipitation, the sample is filtered, rinsed with 0.1% w/v ammonium oxalate, and dried at 100–120oC for 1 hour. The precipitate is transferred to a muffle furnace where it is converted to CaCO3 by drying at 500 ± 25oC until constant weight.
(a) Why is the precipitate of CaC2O4•H2O converted to CaCO3?
(b) In the final step, if the sample is heated at too high of a temperature some CaCO3 may be converted to CaO. What effect would this have on the reported %w/w Ca?
(c) Why is the precipitant, (NH4)2C2O4, added to a hot, acidic solution instead of a cold, alkaline solution?
10. Iron is determined gravimetrically by precipitating as Fe(OH)3 and igniting to Fe2O3. After dissolving a sample in 50 mL of H2O and 10 mL of 6 M HCl, any Fe2+ is converted Fe3+ by oxidizing with 1–2 mL of concentrated HNO3. The sample is heated to remove the oxides of nitrogen and the solution is diluted to 200 mL. After bringing the solution to a boil, Fe(OH)3 is precipitated by slowly adding 1:1 NH3 until the odor of NH3 is detected. The solution is boiled for an additional minute and the precipitate is allowed to settler. The precipitate is then filtered and rinsed with several portions of hot 1% w/v NH4NO3 until no Cl– is found in the wash water. Finally, the precipitate is ignited to constant weight at 500–550oC and weighed as Fe2O3.
(a) If ignition is not carried out under oxidizing conditions (plenty of O2 present), the final product may contain Fe3O4. What effect would this have on the reported %w/w Fe?
(b) The precipitate is washed with a dilute solution of NH4NO3. Why is NH4NO3 added to the wash water?
(c) Why does the procedure call for adding NH3 until the odor of ammonia is detected?
(d) Describe how you might test the filtrate for Cl–.
11. Sinha and Shome described a gravimetric method for molybdenum in which it is precipitated as MoO2(C13H10NO2)2 using n-benzoylphenylhydroxylamine, C13H11NO2, as a precipitant.12 The precipitate is weighed after igniting to MoO3. As part of their study, the authors determined the optimum conditions for the analysis. Samples containing 0.0770 g of Mo were taken through the procedure while varying the temperature, the amount of precipitant added, and the pH of the solution. The solution volume was held constant at 300 mL for all experiments. A summary of their results are shown in the following table.
| Temperature (oC) | Mass(g) of precipitant |
Volume(mL) of 10 M HCl |
Mass (g) of MoO3 |
|
30 |
0.20 |
0.9 |
0.0675 |
|
30 |
0.30 |
0.9 |
0.1014 |
|
30 |
0.35 |
0.9 |
0.1140 |
|
30 |
0.42 |
0.9 |
0.1155 |
|
30 |
0.42 |
0.3 |
0.1150 |
|
30 |
0.42 |
18.0 |
0.1152 |
|
30 |
0.42 |
48.0 |
0.1160 |
|
30 |
0.42 |
75.0 |
0.1159 |
|
50 |
0.42 |
0.9 |
0.1156 |
|
75 |
0.42 |
0.9 |
0.1158 |
|
80 |
0.42 |
0.9 |
0.1129 |
Considering these results, discuss the optimum conditions for determining Mo by this method. Express your results for the precipitant as the minimum %w/v in excess, needed to ensure a quantitative precipitation.
12. A sample of an impure iron ore is approximately 55% w/w Fe. The amount of Fe in the sample is to be determined gravimetrically by isolating it as Fe2O3. What mass of sample do you need to ensure that you isolate at least 1 g of Fe2O3?
13. The concentration of arsenic in an insecticide is determined gravimetrically by precipitating MgNH4AsO4 and isolating Mg2As2O7. Determine the %w/w As2O3 in a 1.627-g sample of insecticide if it yields 106.5 mg of Mg2As2O7.
14. After preparing a sample of alum, K2SO4•Al2(SO4)3•24H2O, a student determined its purity by dissolving a 1.2391-g sample and precipitating the aluminum as Al(OH)3. After filtering, rinsing, and igniting, 0.1357 g of Al2O3 is obtained. What is the purity of the alum preparation?
15. To determine the amount of iron in a dietary supplement, a random sample of 15 tablets weighing a total of 20.505 g was ground into a fine powder. A 3.116-g sample was dissolved and treated to precipitate the iron as Fe(OH)3. The precipitate was collected, rinsed, and ignited to a constant weight as Fe2O3, yielding 0.355 g. Report the iron content of the dietary supplement as g FeSO4•7H2O per tablet.
16. A 1.4639-g sample of limestone was analyzed for Fe, Ca, and Mg. The iron was determined as Fe2O3 yielding 0.0357 g. Calcium was isolated as CaSO4, yielding a precipitate of 1.4058 g, and Mg was isolated as 0.0672 g of Mg2As2O7. Report the amount of Fe, Ca, and Mg in the limestone sample as %w/w Fe2O3, %w/w CaO, and %w/w MgO.
17. The number of ethoxy groups (CH3CH2O–) in an organic compound is determined by the following two reactions.
\[\mathrm{R(CH_2CH_3)}_x+x\mathrm{HI}\rightarrow \mathrm{R(OH)}_x + x\mathrm{CH_3CH_2I}\]
\[\mathrm{CH_3CH_2I+Ag^++H_2O\rightarrow AgI}(s)+\mathrm{CH_3CH_2OH}\]
A 36.92-mg sample of an organic compound with an approximate molecular weight of 176 was treated in this fashion, yielding 0.1478 g of AgI. How many ethoxy groups are there in each molecule of the compound?
18. A 516.7-mg sample containing a mixture of K2SO4 and (NH4)2SO4 was dissolved in water and treated with BaCl2, precipitating the SO42– as BaSO4. The resulting precipitate was isolated by filtration, rinsed free of impurities, and dried to a constant weight, yielding 863.5 mg of BaSO4. What is the %w/w K2SO4 in the sample?
19. The amount of iron and manganese in an alloy can be determined by precipitating the metals with 8-hydroxyquinoline, C9H7NO. After weighing the mixed precipitate, the precipitate is dissolved and the amount of 8-hydroxyquinoline determined by another method. In a typical analysis a 127.3-mg sample of an alloy containing iron, manganese, and other metals was dissolved in acid and treated with appropriate masking agents to prevent an interference from other metals. The iron and manganese were precipitated and isolated as Fe(C9H6NO)3 and Mn(C9H6NO)2, yielding a total mass of 867.8 mg. The amount of 8-hydroxyquinolate in the mixed precipitate was determined to be 5.276 mmol. Calculate the %w/w Fe and %w/w Mn in the alloy.
20. A 0.8612-g sample of a mixture of NaBr, NaI, and NaNO3 was analyzed by adding AgNO3 and precipitating a 1.0186-g mixture of AgBr and AgI. The precipitate was then heated in a stream of Cl2, converting it to 0.7125 g of AgCl. Calculate the %w/w NaNO3 in the sample.
20. The earliest determinations of elemental atomic weights were accomplished gravimetrically. In determining the atomic weight of manganese, a carefully purified sample of MnBr2 weighing 7.16539 g was dissolved and the Br– precipitated as AgBr, yielding 12.53112 g. What is the atomic weight for Mn if the atomic weights for Ag and Br are taken to be 107.868 and 79.904, respectively?
22. While working as a laboratory assistant you prepared 0.4 M solutions of AgNO3, Pb(NO3)2, BaCl2, KI and Na2SO4. Unfortunately, you became distracted and forgot to label the solutions before leaving the laboratory. Realizing your error, you label the solutions A–E and perform all possible binary mixings of the five solutions, obtaining the results shown in Figure 8.16 (key: NP means no precipitate formed, W means a white precipitate formed, and Y means a yellow precipitate formed). Identify solutions A–E.
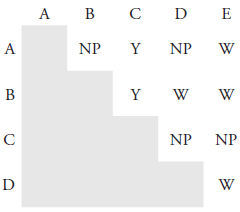
Figure 8.16 Results of the binary mixing of solutions A–E for Problem 8.22.
23. A solid sample has approximately equal amounts of two or more of the following soluble salts: AgNO3, ZnCl2, K2CO3, MgSO4, Ba(C2H3O2)2, and NH4NO3. A sample of the solid, sufficient to give at least 0.04 moles of any single salt, was added to 100 mL of water, yielding a white precipitate and a clear solution. The precipitate was collected and rinsed with water. When a portion of the precipitate was placed in dilute HNO3 it completely dissolved, leaving a colorless solution. A second portion of the precipitate was placed in dilute HCl, yielding a precipitate and a clear solution. Finally, the filtrate from the original precipitate was treated with excess NH3, yielding a white precipitate. Identify the salts that must be present in the sample, the salts that must be absent and the salts for which there is insufficient information to make this determination.13
24. Two methods have been proposed for the analysis of sulfur in impure samples of pyrite, FeS2. Sulfur can be determined in a direct analysis by oxidizing it to SO42– and precipitating it as BaSO4. An indirect analysis is possible if the iron is precipitated as Fe(OH)3 and isolated as Fe2O3. Which of these methods will provide a more sensitive determination for sulfur? What other factors should you consider in choosing between these methods?
25. A sample of impure pyrite known to be approximately 90–95% w/w FeS2 is to be analyzed by oxidizing the sulfur to SO42– and precipitating it as BaSO4. How many grams of the sample must you take to form at least 1 g of BaSO4?
26. A series of samples containing any possible combination of KCl, NaCl, and NH4Cl is to be analyzed by adding AgNO3 and precipitating AgCl. What is the minimum volume of 5% w/v AgNO3 necessary to completely precipitate the chloride in any 0.5-g sample?
27. If a precipitate of known stoichiometry does not form, a gravimetric analysis is still feasible if we can establish experimentally the mole ratio between the analyte and the precipitate. Consider, for example, the precipitation gravimetric analysis of Pb as PbCrO4.14
(a) For each gram of Pb, how many grams of PbCrO4 should form?
(b) In a study of this procedure, Grote found that 1.568 g of PbCrO4 formed for each gram of Pb. What is the apparent stoichiometry between Pb and PbCrO4?
(c) Does failing to account for the actual stoichiometry lead to a positive determinate error or a negative determinate error?
28. Determine the uncertainty for the gravimetric analysis described in Example 8.1. The expected accuracy for a gravimetric method is 0.1–0.2%. What additional sources of error might account for the difference between your estimated uncertainty and the expected accuracy?
29. A 38.63-mg sample of potassium ozonide, KO3, was heated to 70oC for 1 h, undergoing a weight loss of 7.10 mg. A 29.6-mg sample of impure KO3 experiences a 4.86-mg weight loss when treated under similar condition. What is the %w/w KO3 in the sample?
30. The water content of an 875.4-mg sample of cheese was determined with a moisture analyzer. What is the %w/w H2O in the cheese if the final mass was found to be 545.8 mg?
31. Representative Method 8.2 describes a procedure for determining Si in ores and alloys. In this analysis a weight loss of 0.21 g corresponds to 0.1 g of Si. Show that this relationship is correct.
32. The iron in an organometallic compound was determined by treating a 0.4873-g sample with HNO3 and heating to volatilize the organic material. After ignition, the residue of Fe2O3 weighed 0.2091 g.
(a) What is the %w/w Fe in this compound?
(b) The carbon and hydrogen in a second sample of the compound were determined by a combustion analysis. When a 0.5123-g sample was carried through the analysis, 1.2119 g of CO2 and 0.2482 g of H2O were collected. What are the %w/w C and %w/w H in this compound and what is the compound’s empirical formula?
33. A polymer’s ash content is determined by placing a weighed sample in a Pt crucible that has been previously brought to a constant weight. The polymer is melted under gentle heating from a Bunsen burner until the volatile vapor ignites. The polymer is allowed to burn until only a non-combustible residue remains. The residue is brought to constant weight at 800oC in a muffle furnace. The following data were collected during the analysis of two samples of a polymer resin.
|
Polymer A |
g crucible |
g crucible + polymer |
g crucible + ash |
|
replicate 1 |
19.1458 |
21.2287 |
19.7717 |
|
replicate 2 |
15.9193 |
17.9522 |
16.5310 |
|
replicate 3 |
15.6992 |
17.6660 |
16.2909 |
|
Polymer B |
g crucible |
g crucible + polymer |
g crucible + ash |
|
replicate 1 |
19.1457 |
21.0693 |
19.7187 |
|
replicate 2 |
15.6991 |
12.8273 |
16.3327 |
|
replicate 3 |
15.9196 |
17.9037 |
16.5110 |
(a) For each polymer, determine the mean and the standard deviation for the %w/w ash.
(b) Is there any evidence at α = 0.05 for a significant difference between the two polymers? See the appendices for statistical tables.
34. In the presence of water vapor the surface of zirconia, ZrO2, chemically adsorbs H2O, forming surface hydroxyls, ZrOH (additional water is physically adsorbed as H2O). When heated above 200oC, the surface hydroxyls convert to H2O(g), releasing one molecule of water for every two surface hydroxyls. Below 200oC only physically absorbed water is lost. Nawrocki, et al. used thermogravimetry to determine the density of surface hydroxyls on a sample of zirconia that was heated to 700oC and cooled in a desiccator containing humid N2.15 Heating the sample from 200oC to 900oC released 0.006 g of H2O for every gram of dehydroxylated ZrO2. Given that the zirconia had a surface area of 33 m2/g and that one molecule of H2O forms two surface hydroxyls, calculate the density of surface hydroxyls in μmol/m2.
35. The concentration of airborne particulates in an industrial workplace was determined by pulling the air through a single-stage air sampler equipped with a glass-fiber filter. The air was sampled for 20 min at a rate of 75 m3/h. At the end of the sampling period, the filter’s mass was found to have increased by 345.2 mg. What is the concentration of particulates in the air sample in mg/m3 and mg/L?
36. The fat content of potato chips is determined indirectly by weighing a sample before and after extracting the fat with supercritical CO2. The following data were obtained for the analysis of potato chips.16
|
Sample Number |
Initial Mass (g) |
Final Mass (g) |
|
1 |
1.1661 |
0.9253 |
|
2 |
1.1723 |
0.9252 |
|
3 |
1.2525 |
0.9850 |
|
4 |
1.2280 |
0.9562 |
|
5 |
1.2837 |
1.0119 |
(a) Determine the mean and standard deviation for the %w/w fat.
(b) This sample of potato chips is known to have a fat content of 22.7% w/w. Is there any evidence for a determinate error at α = 0.05? See the appendices for statistical tables.
37. Delumyea and McCleary reported results for the %w/w organic material in sediment samples collected at different depths from a cove on the St. Johns River in Jacksonville, FL.17 After collecting a sediment core, they sectioned it into 2-cm increments. Each increment was treated using the following procedure:
(a) The sediment was placed in 50 mL of deionized water and the resulting slurry filtered through preweighed filter paper;
(b) The filter paper and the sediment were placed in a preweighed evaporating dish and dried to a constant weight in an oven at 110oC;
(c) The evaporating dish containing the filter paper and the sediment were transferred to a muffle furnace where the filter paper and any organic material in the sample were removed by ashing;
(d) Finally, the inorganic residue remaining after ashing was weighed.
Using the following data, determine the %w/w organic material as a function of the average depth for each increment.
|
|
Mass (g) of Filter Paper, Dish, and Sediment... |
|||
|
Depth (cm) |
Filter Paper |
Dish |
After Drying |
After Ashing |
|
0–2 |
1.590 |
43.21 |
52.10 |
49.49 |
|
2–4 |
1.745 |
40.62 |
48.83 |
46.00 |
|
4–6 |
1.619 |
41.23 |
52.86 |
47.84 |
|
6–8 |
1.611 |
42.10 |
50.59 |
47.13 |
|
8–10 |
1.658 |
43.62 |
51.88 |
47.53 |
|
10–12 |
1.628 |
43.24 |
49.45 |
45.31 |
|
12–14 |
1.633 |
43.08 |
47.92 |
44.20 |
|
14–16 |
1.630 |
43.96 |
58.31 |
55.53 |
|
16–18 |
1.636 |
43.36 |
54.37 |
52.75 |
38. Yao, et al. recently described a method for the quantitative analysis of thiourea based on its reaction with I2.18
\[\mathrm{CS(NH_2)_2+4I_2+6H_2O\rightarrow (NH_4)_2SO_4+8HI+CO_2}\]
The procedure calls for placing a 100-μL aqueous sample containing thiourea in a 60-mL separatory funnel and adding 10 mL of a pH 7 buffer and 10 mL of 12 μM I2 in CCl4. The contents of the separatory funnel are shaken and the organic and aqueous layers allowed to separate. The organic layer, which contains the excess I2, is transferred to the surface of a piezoelectric crystal on which a thin layer of Au has been deposited. After allowing the I2 to adsorb to the Au, the CCl4 is removed and the crystal’s frequency shift, ∆f, measured. The following data is reported for a series of thiourea standards.
|
[thiourea] (M) |
∆f(Hz) |
[thiourea] (M) |
∆f (Hz) |
|
3.00×10–7 |
74.6 |
1.50×10–6 |
327 |
|
5.00×10–7 |
120 |
2.50×10–6 |
543 |
|
7.00×10–7 |
159 |
3.50×10–6 |
789 |
|
9.00×10–7 |
205 |
5.00×10–6 |
1089 |
(a) Characterize this method with respect to the scale of operation shown in Figure 3.5 of Chapter 3.
(b) Using a regression analysis, determine the relationship between the crystal’s frequency shift and the concentration of thiourea.
(c) If a sample containing an unknown amount of thiourea gives a ∆f of 176 Hz, what is the molar concentration of thiourea in the sample?
(d) What is the 95% confidence interval for the concentration of thiourea in this sample assuming one replicate? See the appendices for statistical tables.
8.5.3 Solutions to Practice Exercises
Practice Exercise 8.1
The solubility reaction for CaC2O4 is
\[\mathrm{CaC_2O_4}(s)\rightleftharpoons \mathrm{Ca^{2+}}(aq)+\mathrm{C_2O_4^{2-}}(aq)\]
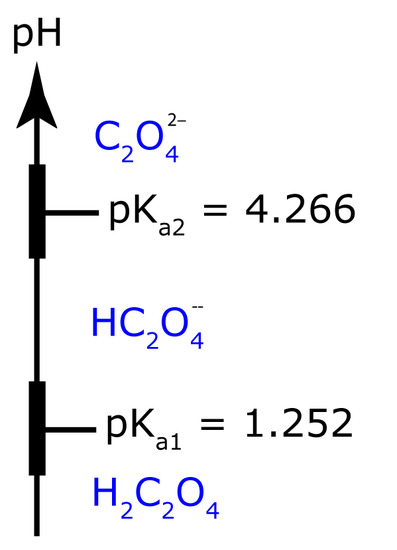
To minimize solubility, the pH needs to be basic enough that oxalate, C2O42–, does not react to form HC2O4– or H2C2O4. The ladder diagram for oxalic acid, including approximate buffer ranges, is shown in Figure 8.17. Maintaining a pH greater than 5.3 ensures that C2O42– is the only important form of oxalic acid in solution, minimizing the solubility of CaC2O4.
Figure 8.17 pH ladder diagram for oxalic acid, H2C2O4.
Click here to return to the chapter.
Practice Exercise 8.2
A conservation of mass requires that all the zinc in the alloy is found in the final product, Zn2P2O7. We know that there are 2 moles of Zn per mole of Zn2P2O7; thus
\[\mathrm{0.1163\;g\;Zn_2P_2O_7\times\dfrac{2\;mol\;Zn}{304.72\;g\;Zn_2P_2O_7}\times\dfrac{65.39\;g\;Zn}{mol\;Zn}=4.991\times10^{-2}\;g\;Zn}\]
This is the mass of Zn in 25% of the sample (a 25.00 mL portion of the 100.0 mL total volume). The %w/w Zn, therefore, is
\[\mathrm{\dfrac{4.991\times10^{-2}\;g\;Zn\times4}{0.7336\;g\;sample}\times100=27.22\%\;w/w\;Zn}\]
For copper, we find that
\[\mathrm{0.1163\;g\;CuSCN\times\dfrac{1\;mol\;Cu}{121.64\;g\;CuSCN}\times\dfrac{63.55\;g\;Cu}{mol\;Cu}=0.1249\;g\;Cu}\]
\[\mathrm{\dfrac{0.1249\;g\;Cu\times4}{0.7336\;g\;sample}\times100=67.88\%\;w/w\;Cu}\]
Click here to return to the chapter.
Practice Exercise 8.3
The masses of the solids provide us with the following equations
\[\textrm{g NaCl + g KCl = 0.2692 g}\]
\[\mathrm{(g\;KClO_4)_{NaCl}+(g\;KClO_4)_{KCl}=0.5713\;g}\]
where (g KClO4)NaCl and (g KClO4)KCl are the masses of KClO4 from the reaction of HClO4 with NaCl and KCl. With two equations and four unknowns, we need two additional equations to solve the problem. A conservation of mass requires that all the chlorine in NaCl is found in the (KClO4)NaCl; thus
\[\mathrm{(g\;KClO_4)_{NaCl}=g\;NaCl\times\dfrac{1\;mol\;Cl}{58.44\;g\;NaCl}\times\dfrac{138.55\;g\;KClO_4}{mol\;Cl}}\]
\[\mathrm{(g\;KClO_4)_{NaCl}=2.3708\times g\;NaCl}\]
Using the same approach for KCl gives
\[\mathrm{(g\;KClO_4)_{KCl}=g\;KCl\times\dfrac{1\;mol\;Cl}{74.55\;g\;KCl}\times\dfrac{138.55\;g\;KClO_4}{mol\;Cl}}\]
\[\mathrm{(g\;KClO_4)_{KCl}=1.8584\times g\;KCl}\]
Substituting the equations for (g KClO4)NaCl and (g KClO4)KCl into the equation for their combined masses leaves us with two equations and two unknowns.
\[\textrm{g NaCl + g KCl = 0.2692 g}\]
\[\mathrm{2.3708\times g\;NaCl+1.8584\times g\;KCl=0.5713\;g}\]
Multiplying the first equation by 1.8584 and subtracting the second equation gives
\[\mathrm{-0.5124\times g\;NaCl=-0.07102\;g}\]
\[\textrm{g NaCl = 0.1386 g}\]
To report the %w/w Na2O in the sample, we use a conservation of mass on sodium.
\[\mathrm{0.1386\;g\;NaCl\times\dfrac{1\;mol\;Na}{58.44\;g\;NaCl}\times\dfrac{61.98\;g\;Na_2O}{2\;mol\;Na}=0.07350\;g\;Na_2O}\]
\[\mathrm{\dfrac{0.07350\;g\;Na_2O}{0.8143\;g\;sample}\times100=9.026\%\;w/w\;Na_2O}\]
Click here to return to the chapter.
Practice Exercise 8.4
To find the mass of (NH4)3PO4•12MoO3 producing 0.600 g of PbMoO3, we first use a conservation of mass for molybdenum; thus
\[\mathrm{0.600\;g\;PbMoO_3\times\dfrac{1\;mol\;Mo}{351.14\;g\;PbMoO_3}\times\dfrac{1876.38\;g\;(NH_4)_3PO_4\cdot 12MoO_3}{12\;mol\;Mo}=0.2672\;g\;(NH_4)_3PO_4\cdot 12MoO_3}\]
Next, to convert this mass of (NH4)3PO4•12MoO3 to a mass of Na3PO4, we use a conservation of mass on PO43–.
\[\mathrm{0.2672\;g\;(NH_4)_3PO_4\cdot 12MoO_3\times\dfrac{1\;mol\;PO_4^{3-}}{1876.38\;g\;(NH_4)_3PO_4\cdot 12MoO_3}\times\dfrac{163.94\;g\;Na_3PO_4}{mol\;PO_4^{3-}}=0.02335\;g\;Na_3PO_4}\]
Finally, we convert this mass of Na3PO4 to the corresponding mass of sample.
\[\mathrm{0.02335\;g\;Na_3PO_4\times\dfrac{100\;g\;sample}{12.5\;g\;Na_3PO_4}=0.187\;g\;sample}\]
A sample of 0.187 g is sufficient to guarantee 0.600 g of PbMoO3. If a sample contains more than 12.5% Na3PO4, then a 0.187-g sample will produce more than 0.600 g of PbMoO3.
Click here to return to the chapter.
Practice Exercise 8.5
To determine which form has the greatest sensitivity, we use a conservation of mass for iron to find the relationship between the precipitate’s mass and the mass of iron.
\[\mathrm{g\;FeO=g\;Fe\times\dfrac{1\;mol\;Fe}{55.85\;g\;Fe}\times\dfrac{71.85\;g\;FeO}{mol\;Fe}= 1.286\times g\;Fe}\]
\[\mathrm{g\;Fe_2O_3=g\;Fe\times\dfrac{1\;mol\;Fe}{55.85\;g\;Fe}\times\dfrac{159.70\;g\;Fe_2O_3}{2\;mol\;Fe}=1.430\times g\;Fe}\]
\[\mathrm{g\;Fe_3O_4=g\;Fe\times\dfrac{1\;mol\;Fe}{55.85\;g\;Fe}\times\dfrac{231.55\;g\;Fe_3O_4}{3\;mol\;Fe}=1.382\times\;g\;Fe}\]
Of the three choices, the greatest sensitivity is obtained with Fe2O3 because it provides the largest value for k.
Click here to return to the chapter.
Practice Exercise 8.6
From 100–250oC the sample loses 13.8% of its mass, or a loss of
\[\mathrm{0.138\times130.35\;g/mol=18.0\;g/mol}\]
consistent with the loss of H2O(g), leaving a residue of MgC2O4. From 350–550oC the sample loses 55.23% of its original mass, or a loss of
\[\mathrm{0.5523\times130.35\;g/mol=71.99\;g/mol}\]
This weight loss is consistent with the simultaneous loss of CO(g) and CO2(g), leaving a residue of MgO.
We can analyze the mixture by heating a portion of the sample to 300oC, 600oC, and 1000oC, recording the mass at each temperature. The loss of mass between 600oC and 1000oC, ∆m2, is due to the loss of CO2(g) from the decomposition of CaCO3 to CaO, and is proportional to the mass of CaC2O4•H2O in the sample.
\[\mathrm{g\;CaC_2O_4\cdot H_2O}=\Delta m_2\times\mathrm{\dfrac{1\;mol\;CO_2}{44.01\;g\;CO_2}\times\dfrac{146.11\;g\;CaC_2O_4\cdot H_2O}{mol\;CO_2}}\]
The change in mass between 300oC and 600oC, ∆m1, is due to the loss of CO(g) from CaC2O4•H2O and the loss of CO(g) and CO2(g) from MgC2O4•H2O. Because we already know the amount of CaC2O4•H2O in the sample, we can calculate its contribution to ∆m1.
\[(\Delta m_1)\mathrm{_{Ca}=g\;CaC_2O_4\cdot H_2O\times\dfrac{1\;mol\;CO}{146.11\;g\;CaC_2O_4\cdot H_2O}\times\dfrac{28.01\;g\;CO}{mol\;CO}}\]
The change in mass due to the decomposition of MgC2O4•H2O
\[(\Delta m_1)_\textrm{Mg}=(\Delta m_1)-(\Delta m_1)_\textrm{Ca}\]
provides the mass of MgC2O4•H2O in the sample.
\[\mathrm{g\;MgC_2O_4\cdot H_2O}=(\Delta m_1)_\textrm{Mg}\mathrm{\times\dfrac{1\;mol\;(CO + CO_2)}{130.35\;g\;MgC_2O_4\cdot H_2O}\times\dfrac{78.02\;g\;(CO+CO_2)}{1\;mol\;(CO+CO_2)}}\]
Click here to return to the chapter.
Practice Exercise 8.7
In Practice Exercise 8.6 we developed an equation for the mass of CaC2O4•H2O in a mixture of CaC2O4•H2O, MgC2O4•H2O, and inert materials. Adapting this equation to a sample containing CaC2O4, CaC2O, and inert materials is easy; thus
\[\mathrm{g\;CaC_2O_4=(0.1794\;g-0.1294\;g)\times\dfrac{1\;mol\;CO_2}{44.01\;g\;CO_2}\times\dfrac{128.10\;g\;CaC_2O_4}{mol\;CO_2}=0.1455\;g\;CaC_2O_4}\]
The %w/w CaC2O4 in the sample is
\[\mathrm{\dfrac{0.1455\;g\;CaC_2O_4}{0.3317\;g\;sample}\times100=43.86\%\;w/w\;CaC_2O_4}\]
Click here to return to the chapter.