5.1: Analytical Signals
- Page ID
- 220688
To standardize an analytical method we use standards that contain known amounts of analyte. The accuracy of a standardization, therefore, depends on the quality of the reagents and the glassware we use to prepare these standards. For example, in an acid–base titration the stoichiometry of the acid–base reaction defines the relationship between the moles of analyte and the moles of titrant. In turn, the moles of titrant is the product of the titrant’s concentration and the volume of titrant used to reach the equivalence point. The accuracy of a titrimetric analysis, therefore, is never better than the accuracy with which we know the titrant’s concentration.
See Chapter 9 for a thorough discussion of titrimetric methods of analysis.
Primary and Secondary Standards
There are two categories of analytical standards: primary standards and secondary standards. A primary standard is a reagent that we can use to dispense an accurately known amount of analyte. For example, a 0.1250-g sample of K2Cr2O7 contains \(4.249 \times 10^{-4}\) moles of K2Cr2O7. If we place this sample in a 250-mL volumetric flask and dilute to volume, the concentration of K2Cr2O7 in the resulting solution is \(1.700 \times 10^{-3} \text{ M}\). A primary standard must have a known stoichiometry, a known purity (or assay), and it must be stable during long-term storage. Because it is difficult to establishing accurately the degree of hydration, even after drying, a hydrated reagent usually is not a primary standard.
Reagents that do not meet these criteria are secondary standards. The concentration of a secondary standard is determined relative to a primary standard. Lists of acceptable primary standards are available (see, for instance, Smith, B. W.; Parsons, M. L. J. Chem. Educ. 1973, 50, 679–681; or Moody, J. R.; Green- burg, P. R.; Pratt, K. W.; Rains, T. C. Anal. Chem. 1988, 60, 1203A–1218A). Appendix 8 provides examples of some common primary standards.
NaOH is one example of a secondary standard. Commercially available NaOH contains impurities of NaCl, Na2CO3, and Na2SO4, and readily absorbs H2O from the atmosphere. To determine the concentration of NaOH in a solution, we titrate it against a primary standard weak acid, such as potassium hydrogen phthalate, KHC8H4O4.
Other Reagents
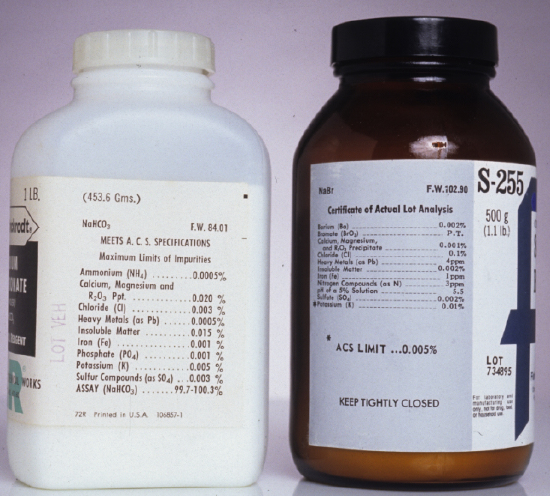
Preparing a standard often requires additional reagents that are not primary standards or secondary standards, such as a suitable solvent or reagents needed to adjust the standard’s matrix. These solvents and reagents are potential sources of additional analyte, which, if not accounted for, produce a determinate error in the standardization. If available, reagent grade chemicals that conform to standards set by the American Chemical Society are used [Committee on Analytical Reagents, Reagent Chemicals, 8th ed., American Chemical Society: Washington, D. C., 1993]. The label on the bottle of a reagent grade chemical (Figure \(\PageIndex{1}\)) lists either the limits for specific impurities or provides an assay for the impurities. We can improve the quality of a reagent grade chemical by purifying it, or by conducting a more accurate assay. As discussed later in the chapter, we can correct for contributions to Stotal from reagents used in an analysis by including an appropriate blank determination in the analytical procedure.
Preparing a Standard Solution
It often is necessary to prepare a series of standards, each with a different concentration of analyte. We can prepare these standards in two ways. If the range of concentrations is limited to one or two orders of magnitude, then each solution is best prepared by transferring a known mass or volume of the pure standard to a volumetric flask and diluting to volume.
When working with a larger range of concentrations, particularly a range that extends over more than three orders of magnitude, standards are best prepared by a serial dilution from a single stock solution. In a serial dilution we prepare the most concentrated standard and then dilute a portion of that solution to prepare the next most concentrated standard. Next, we dilute a portion of the second standard to prepare a third standard, continuing this process until we have prepared all of our standards. Serial dilutions must be prepared with extra care because an error in preparing one standard is passed on to all succeeding standards.


