5.4: Predicting Reaction Direction
- Page ID
- 164759
Skills to Develop
- To determine the value of the equilibrium constant given experimental data.
- To predict in which direction a reaction will proceed.
We previously saw that knowing the magnitude of the equilibrium constant under a given set of conditions allows chemists to predict the extent of a reaction. Often, however, chemists must decide whether a system has reached equilibrium or if the composition of the mixture will continue to change with time. In this section, we describe how to quantitatively analyze the composition of a reaction mixture to make this determination.
Calculating the Equilibrium Constant
In order to determine the value of K for a reaction, we must have experimental data on the reaction conditions at equilibrium. For example, the equilibrium constant for the decomposition of \(CaCO_{3(s)}\) to \(CaO_{(s)}\) and \(CO_{2(g)}\) is \(K = [CO_2]\). At 800°C, the concentration of \(CO_2\) in equilibrium with solid \(CaCO_3\) and \(CaO\) is known to be \(2.5 \times 10^{-3}\; M\). Thus K at 800°C is \(2.5 \times 10^{-3}\). (Remember that equilibrium constants are unitless.)
A more complex example of this type of problem is the conversion of n-butane, an additive used to increase the volatility of gasoline, into isobutane (2-methylpropane).
This reaction can be written as follows:
and the equilibrium constant \(K = [\text{isobutane}]/[\text{n-butane}]\). At equilibrium, a mixture of n-butane and isobutane at room temperature was found to contain 0.041 M isobutane and 0.016 M n-butane. Substituting these concentrations into the equilibrium constant expression,
Thus the equilibrium constant for the reaction as written is 2.6.
Example \(\PageIndex{1}\)
The reaction between gaseous sulfur dioxide and oxygen is a key step in the industrial synthesis of sulfuric acid:
A mixture of \(SO_2\) and \(O_2\) was maintained at 800 K until the system reached equilibrium. The equilibrium mixture contained
- \(5.0 \times 10^{-2}\; M\; SO_3\),
- \(3.5 \times 10^{-3}\; M\; O_2\), and
- \(3.0 \times 10^{-3}\; M\; SO_2\).
Calculate \(K\) and \(K_p\) at this temperature.
Given: balanced equilibrium equation and composition of equilibrium mixture
Asked for: equilibrium constant
Strategy
Write the equilibrium constant expression for the reaction. Then substitute the appropriate equilibrium concentrations into this equation to obtain \(K\).
SOLUTION
Substituting the appropriate equilibrium concentrations into the equilibrium constant expression,
To solve for \(K_p\), we use the relationship derived previously
\[K_p = K(RT)^{Δn} \]
where \(Δn = 2 − 3 = −1\):
\[K_p=K(RT)^{Δn}\nonumber\]
\[K_p=7.9 \times 10^4 [(0.08206\; L⋅atm/mol⋅K)(800 K)]^{−1}\nonumber\]
\[K_p=1.2 \times 10^3\nonumber\]
Exercise \(\PageIndex{1}\)
Hydrogen gas and iodine react to form hydrogen iodide via the reaction
A mixture of \(H_2\) and \(I_2\) was maintained at 740 K until the system reached equilibrium. The equilibrium mixture contained
- \(1.37\times 10^{−2}\; M\; HI\),
- \(6.47 \times 10^{−3}\; M\; H_2\), and
- \(5.94 \times 10^{-4}\; M\; I_2\).
Calculate \(K\) and \(K_p\) for this reaction.
- Answer
-
\(K = 48.8\) and \(K_p = 48.8\)
Chemists are not often given the concentrations of all the substances, and they are not likely to measure the equilibrium concentrations of all the relevant substances for a particular system if they don't have to. In such cases, we can obtain the equilibrium concentrations from the initial concentrations of the reactants and the balanced chemical equation for the reaction, as long as the equilibrium concentration of one of the substances is known. Example \(\PageIndex{2}\) shows one way to do this, using the "ICE table" method. In this useful method, we consider the Initial concentrations of reactants and products, the Change that occurs, and the final Equilibrium conditions in order to organize the problem.
Example \(\PageIndex{2}\)
A 1.00 mol sample of \(NOCl\) was placed in a 2.00 L reactor and heated to 227°C until the system reached equilibrium. The contents of the reactor were then analyzed and found to contain 0.056 mol of \(Cl_2\). Calculate \(K\) at this temperature. The equation for the decomposition of \(NOCl\) to \(NO\) and \(Cl_2\) is as follows:
\[2 NOCl_{(g)} \rightleftharpoons 2NO_{(g)}+Cl_{2(g)}\nonumber\]
Given: balanced equilibrium equation, amount of reactant, volume, and amount of one product at equilibrium
Asked for: \(K\)
Strategy:
- Write the equilibrium constant expression for the reaction. Construct a table showing the initial concentrations, the changes in concentrations, and the final concentrations (as initial concentrations plus changes in concentrations).
- Calculate all possible initial concentrations from the data given and insert them in the table.
- Use the coefficients in the balanced chemical equation to obtain the changes in concentration of all other substances in the reaction. Insert those concentration changes in the table.
- Obtain the final concentrations by summing the columns. Calculate the equilibrium constant for the reaction.
SOLUTION
A The first step in any such problem is to balance the chemical equation for the reaction (if it is not already balanced) and use it to derive the equilibrium constant expression. In this case, the equation is already balanced, and the equilibrium constant expression is as follows:
\[K=\dfrac{[NO]^2[Cl_2]}{[NOCl]^2}\nonumber\]
To obtain the concentrations of \(NOCl\), \(NO\), and \(Cl_2\) at equilibrium, we construct an ICE table showing what is known and what needs to be calculated. We begin by writing the balanced chemical equation at the top of the table, followed by three lines corresponding to the initial concentrations, the changes in concentrations required to get from the initial to the final state, and the final equilibrium concentrations.
\[2 NOCl_{(g)} \rightleftharpoons 2NO_{(g)}+Cl_{2(g)}\nonumber\]
| ICE | \([NOCl]\) | \([NO]\) | \([Cl_2]\) |
|---|---|---|---|
| Initial | |||
| Change | |||
| Equilibrium |
B Initially, the system contains 1.00 mol of \(NOCl\) in a 2.00 L container. Thus \([NOCl]_i = 1.00\; mol/2.00\; L = 0.500\; M\). The initial concentrations of \(NO\) and \(Cl_2\) are \(0\; M\) because initially no products are present. Moreover, we are told that at equilibrium the system contains 0.056 mol of \(Cl_2\) in a 2.00 L container, so \([Cl_2]_f = 0.056 \;mol/2.00 \;L = 0.028\; M\). We insert these values into the following table:
\[2 NOCl_{(g)} \rightleftharpoons 2NO_{(g)}+Cl_{2(g)}\nonumber\]
| ICE | \([NOCl]\) | \([NO]\) | \([Cl_2]\) |
|---|---|---|---|
| Initial | 0.500 | 0 | 0 |
| Change | |||
| Equilibrium | 0.028 |
C We use the stoichiometric relationships given in the balanced chemical equation to find the change in the concentration of \(Cl_2\), the substance for which initial and final concentrations are known:
\[Δ[Cl_2] = 0.028 \;M_{(final)} − 0.00\; M_{(initial)}] = +0.028\; M\nonumber\]
According to the coefficients in the balanced chemical equation, 2 mol of \(NO\) are produced for every 1 mol of \(Cl_2\), so the change in the \(NO\) concentration is as follows:
\[Δ[NO]=\left(\dfrac{0.028\; \cancel{mol \;Cl_2}}{ L}\right)\left(\dfrac{2\; mol\; NO}{1 \cancel{\;mol \;Cl_2}}\right)=0.056\; M\nonumber\]
Similarly, 2 mol of \(NOCl\) are consumed for every 1 mol of \(Cl_2\) produced, so the change in the \(NOCl\) concentration is as follows:
\[Δ[NOCl]= \left(\dfrac{0.028\; \cancel{mol\; Cl_2}}{L}\right) \left(\dfrac{−2\; mol \;NOCl}{1\; \cancel{mol\; Cl_2}} \right) = -0.056 \;M\nonumber\]
We insert these values into our table:
\[2 NOCl_{(g)} \rightleftharpoons 2NO_{(g)}+Cl_{2(g)}\nonumber\]
| ICE | \([NOCl]\) | \([NO]\) | \([Cl_2]\) |
|---|---|---|---|
| Initial | 0.500 | 0 | 0 |
| Change | −0.056 | +0.056 | +0.028 |
| Equilibrium | 0.028 |
D We sum the numbers in the \([NOCl]\) and \([NO]\) columns to obtain the final concentrations of \(NO\) and \(NOCl\):
\[[NO]_f = 0.000\; M + 0.056 \;M = 0.056\; M\nonumber\]
\[[NOCl]_f = 0.500\; M + (−0.056\; M) = 0.444 M\nonumber\]
We can now complete the table:
\[2 NOCl_{(g)} \rightleftharpoons 2NO_{(g)}+Cl_{2(g)}\nonumber\]
| ICE | \([NOCl] | \([NO]\) | \([Cl_2]\) |
|---|---|---|---|
| initial | 0.500 | 0 | 0 |
| change | −0.056 | +0.056 | +0.028 |
| equilibrium | 0.444 | 0.056 | 0.028 |
We can now calculate the equilibrium constant for the reaction:
\[K=\dfrac{[NO]^2[Cl_2]}{[NOCl]^2}=\dfrac{(0.056)^2(0.028)}{(0.444)^2}=4.5 \times 10^{−4}\nonumber\]
Exercise \(\PageIndex{2}\)
The German chemist Fritz Haber (1868–1934; Nobel Prize in Chemistry 1918) was able to synthesize ammonia (\(NH_3\)) by reacting \(0.1248\; M \;H_2\) and \(0.0416\; M \;N_2\) at about 500°C. At equilibrium, the mixture contained 0.00272 M \(NH_3\). What is \(K\) for the reaction
\[N_2+3H_2 \rightleftharpoons 2NH_3\nonumber\]
at this temperature? What is \(K_p\)?
- Answer
-
\(K = 0.105\) and \(K_p = 2.61 \times 10^{-5}\)
The Reaction Quotient
In many cases, a reaction may not have reached equilibrium - it must proceed either forward or backward to reach it. Which direction will a reaction proceed? To determine this, chemists use a quantity called the reaction Quotient (Q). The expression for the reaction Quotient has precisely the same form as the equilibrium constant expression, except that \(Q\) may be derived from a set of values measured at any time during the reaction of any mixture of the reactants and the products, regardless of whether the system is at equilibrium. Therefore, for the following general reaction:
the reaction quotient is defined as follows:
\[Q=\dfrac{[C]^c[D]^d}{[A]^a[B]^b} \label{15.6.1}\]
To understand how information is obtained using a reaction Quotient, consider the dissociation of dinitrogen tetroxide to nitrogen dioxide,
\[N_2O_{4(g)} \rightleftharpoons 2NO_{2(g)}\]
for which \(K = 4.65 \times 10^{−3}\) at 298 K. We can write \(Q\) for this reaction as follows:
The following table lists data from three experiments in which samples of the reaction mixture were obtained and analyzed at equivalent time intervals, and the corresponding values of \(Q\) were calculated for each. Each experiment begins with different proportions of product and reactant:
| Experiment | \([NO_2]\; (M)\) | \([N_2O_4]\; (M)\) | \(Q = \dfrac{[NO^2]^2}{[N^2O^4]}\) |
|---|---|---|---|
| 1 | 0 | 0.0400 | \(\dfrac{0^2}{0.0400}=0\) |
| 2 | 0.0600 | 0 | \(\dfrac{(0.0600)^2}{0}=\text{undefined}\) |
| 3 | 0.0200 | 0.0600 | \(\dfrac{(0.0200)^2}{0.0600}=6.67 \times 10^{−3}\) |
As these calculations demonstrate, \(Q\) can have any numerical value between 0 and infinity (undefined); that is, \(Q\) can be greater than, less than, or equal to K.
Comparing the magnitudes of \(Q\) and K enables us to determine whether a reaction mixture is already at equilibrium and, if it is not, predict how its composition will change with time to reach equilibrium (i.e., whether the reaction will proceed to the right or to the left as written). All you need to remember is that the composition of a system not at equilibrium will change in a way that makes \(Q\) approach K. If \(Q = K\), for example, then the system is already at equilibrium, and no further change in the composition of the system will occur unless the conditions are changed. If \(Q < K\), then the ratio of the concentrations of products to the concentrations of reactants is less than the ratio at equilibrium. Therefore, the reaction will proceed to the right as written, forming products at the expense of reactants. Conversely, if \(Q > K\), then the ratio of the concentrations of products to the concentrations of reactants is greater than at equilibrium, so the reaction will proceed to the left as written, forming reactants at the expense of products. These points are illustrated graphically in Figure \(\PageIndex{1}\).
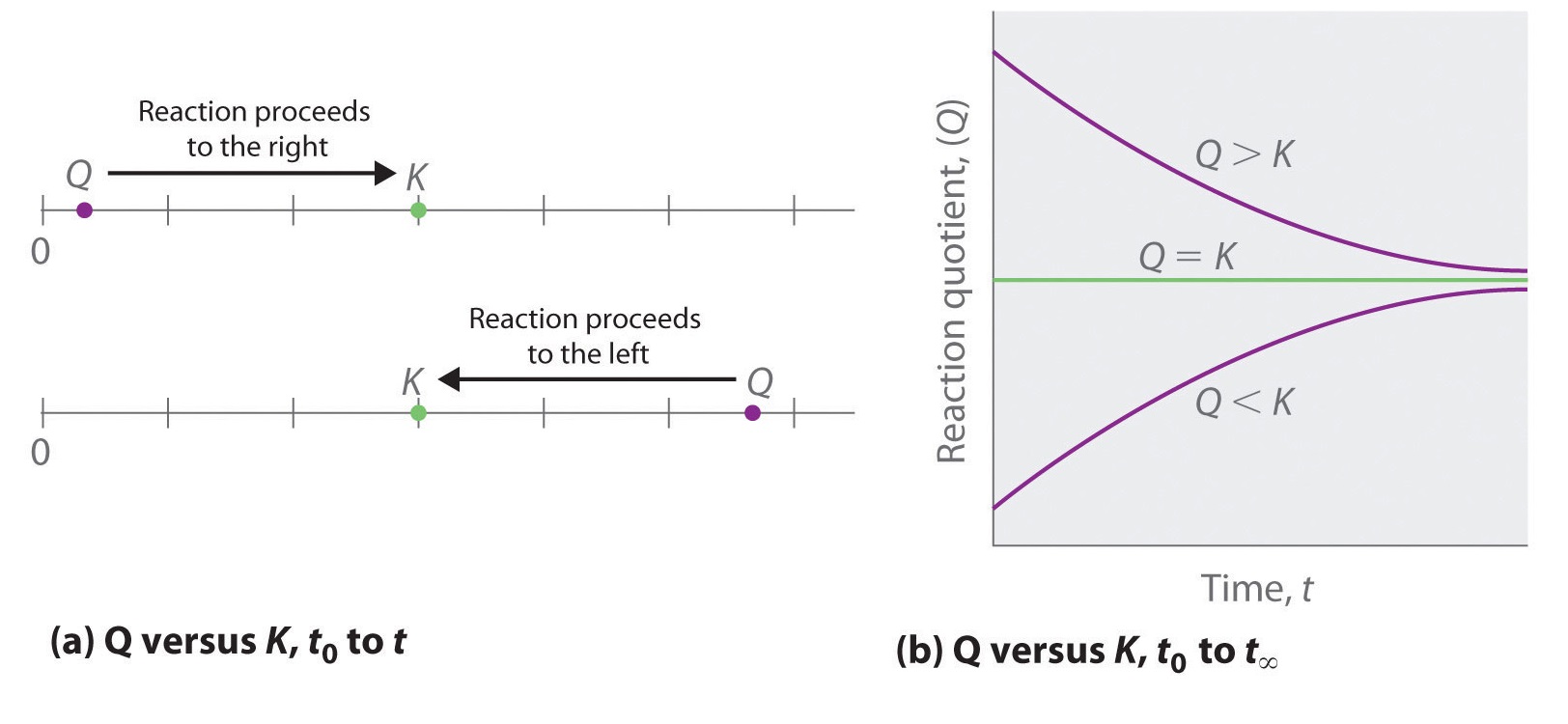
If \(Q < K\), the reaction will proceed to the right (forward) as written.
If \(Q > K\), the reaction will proceed to the left (backward) as written.
If \(Q = K\), then the system is at equilibrium.
Example \(\PageIndex{1}\)
At elevated temperatures, methane (\(CH_4\)) reacts with water to produce hydrogen and carbon monoxide in what is known as a steam-reforming reaction:
\[CH_{4(g)}+H_2O_{(g)} \rightleftharpoons CO_{(g)}+3H_{2(g)}\]
\(K = 2.4 \times 10^{−4}\) at 900 K. Huge amounts of hydrogen are produced from natural gas in this way and are then used for the industrial synthesis of ammonia. If \(1.2 \times 10^{−2}\) mol of \(CH_4\), 8.0 × 10−3 mol of \(H_2O\), \(1.6 \times 10^{−2}\) mol of \(CO\), and \(6.0 \times 10^{−3}\) mol of \(H_2\) are placed in a 2.0 L steel reactor and heated to 900 K, will the reaction be at equilibrium or will it proceed to the right to produce \(CO\) and \(H_2\) or to the left to form \(CH_4\) and \(H_2O\)?
Given: balanced chemical equation, K, amounts of reactants and products, and volume
Asked for: direction of reaction
Strategy:
- Calculate the molar concentrations of the reactants and the products.
- Use Equation \(\ref{15.6.1}\) to determine \(Q\) . Compare \(Q\) and \(K\) to determine in which direction the reaction will proceed.
Solution:
A We must first find the initial concentrations of the substances present. For example, we have \(1.2 \times 10^{−2} mol\) of \(CH_4\) in a 2.0 L container, so
\[[CH_4]=\dfrac{1.2\times 10^{−2} mol}{2.0\; L}=6.0 \times 10^{−3} M\]
We can calculate the other concentrations in a similar way:
- \([H_2O] = 4.0 \times 10^{−3} M\),
- \([CO] = 8.0 \times 10^{−3} M\), and
- \([H_2] = 3.0 \times 10^{−3} M\).
B We now compute \(Q\) and compare it with \(K\):
\[Q=\dfrac{[CO][H_2]^3}{[CH_4][H_2O}=\dfrac{(8.0 \times 10^{−3})(3.0 \times 10^{−3})^3}{(6.0\times 10^{−3})(4.0 \times 10^{−3})}=9.0 \times 10^{−6}\]
Because \(K = 2.4 \times 10^{−4}\), we see that \(Q < K\). Thus the ratio of the concentrations of products to the concentrations of reactants is less than the ratio for an equilibrium mixture. The reaction will therefore proceed to the right as written, forming \(H_2\) and \(CO\) at the expense of \(H_2O\) and \(CH_4\).
Exercise \(\PageIndex{2}\)
In the water–gas shift reaction introduced in Example \(\PageIndex{1}\), carbon monoxide produced by steam-reforming reaction of methane reacts with steam at elevated temperatures to produce more hydrogen:
\[CO_{(g)}+H_2O_{(g)} \rightleftharpoons CO_{2(g)}+H_{2(g)}\]
\(K = 0.64\) at 900 K. If 0.010 mol of both \(CO\) and \(H_2O\), 0.0080 mol of \(CO_2\), and 0.012 mol of \(H_2\) are injected into a 4.0 L reactor and heated to 900 K, will the reaction proceed to the left or to the right as written?
- Answer
-
\(Q = 0.96\). Since (Q > K), so the reaction will proceed to the left, and \(CO\) and \(H_2O\) will form.
Summary
Equilibrium constants can be calculated if the concentrations of reactants and products at equilibrium are known. The reaction Quotient (Q) is used to determine whether a system is at equilibrium and if it is not, to predict the direction of reaction. The reaction Quotient (\(Q\) or \(Q_p\)) has the same form as the equilibrium constant expression, but it is derived from concentrations obtained at any time. When a reaction system is at equilibrium, \(Q = K\).

