10.6: Orbital Hybridization
- Page ID
- 98650
The localized valence bond theory uses a process called hybridization, in which atomic orbitals that are similar in energy but not equivalent are combined mathematically to produce sets of equivalent orbitals that are properly oriented to form bonds. These new combinations are called hybrid atomic orbitals because they are produced by combining (hybridizing) two or more atomic orbitals from the same atom.
Hybridization of s and p Orbitals
In BeH2, we can generate two equivalent orbitals by combining the 2s orbital of beryllium and any one of the three degenerate 2p orbitals. By taking the sum and the difference of Be 2s and 2pz atomic orbitals, for example, we produce two new orbitals with major and minor lobes oriented along the z-axes, as shown in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): The position of the atomic nucleus with respect to an sp hybrid orbital. The nucleus is actually located slightly inside the minor lobe, not at the node separating the major and minor lobes.
Because the difference A − B can also be written as A + (−B), in Figure \(\PageIndex{2}\) and subsequent figures we have reversed the phase(s) of the orbital being subtracted, which is the same as multiplying it by −1 and adding. This gives us Equation \ref{9.5.1b}, where the value \(\frac{1}{\sqrt{2}}\) is needed mathematically to indicate that the 2s and 2p orbitals contribute equally to each hybrid orbital.
\[sp = \dfrac{1}{\sqrt{2}} (2s + 2p_z) \label{9.5.1a}\]
and
\[sp = \dfrac{1}{\sqrt{2}} (2s - 2p_z) \label{9.5.1b}\]
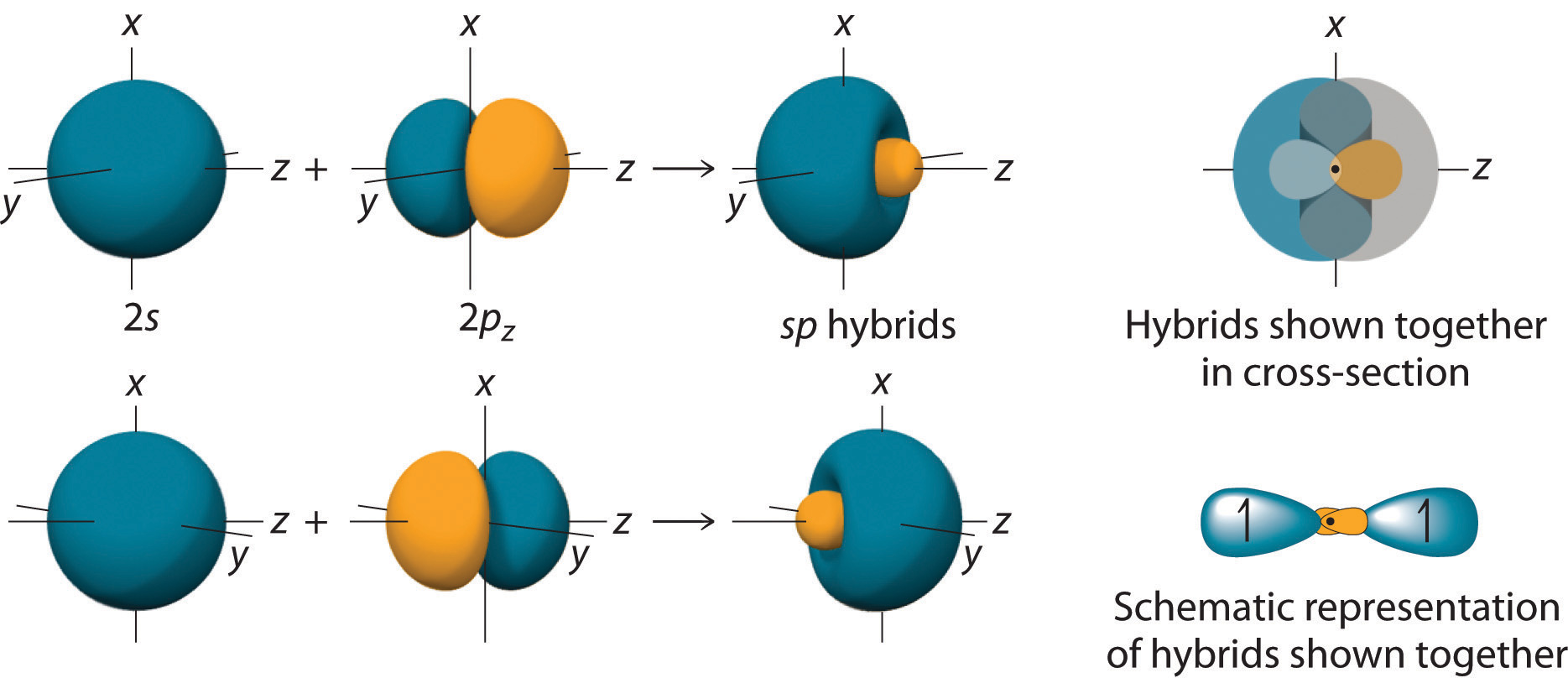
Figure \(\PageIndex{2}\): The Formation of sp Hybrid Orbitals. Taking the sum and difference of an ns and an np atomic orbital where n = 2 gives two equivalent sp hybrid orbitals oriented at 180° to each other.
The nucleus resides just inside the minor lobe of each orbital. In this case, the new orbitals are called sp hybrids because they are formed from one s and one p orbital. The two new orbitals are equivalent in energy, and their energy is between the energy values associated with pure s and p orbitals, as illustrated in this diagram:
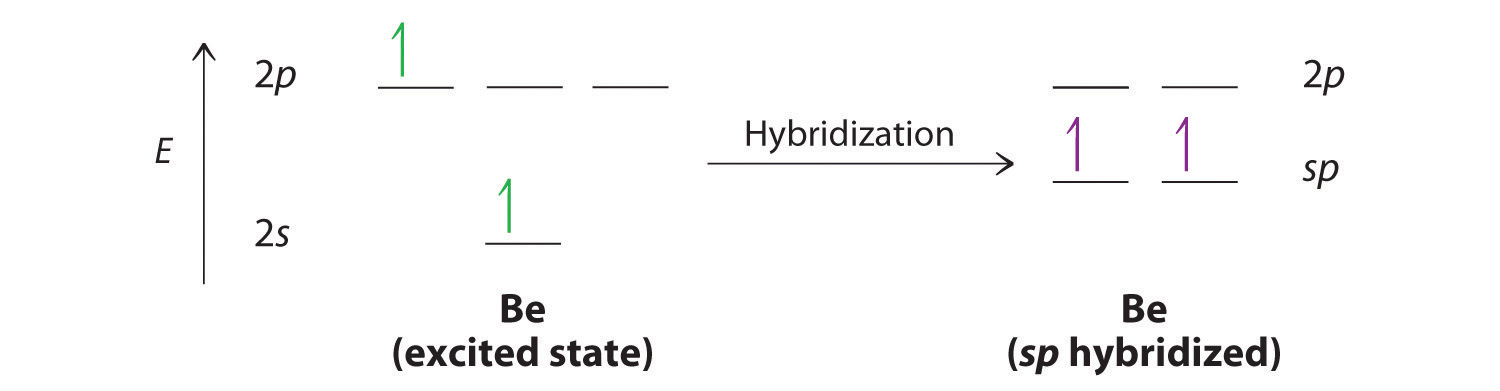
Each singly occupied sp hybrid orbital can now form an electron-pair bond with the singly occupied 1s atomic orbital of one of the H atoms. As shown in Figure \(\PageIndex{3}\). each sp orbital on Be has the correct orientation for the major lobes to overlap with the 1s atomic orbital of an H atom. The formation of two energetically equivalent Be–H bonds produces a linear \(BeH_2\) molecule. Thus valence bond theory does what neither the Lewis electron structure nor the VSEPR model is able to do; it explains why the bonds in \(BeH_2\) are equivalent in energy and why \(BeH_2\) has a linear geometry.
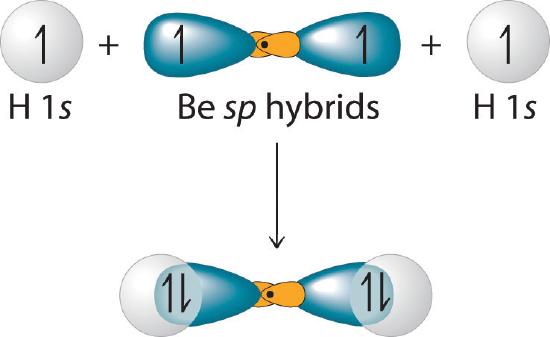
Figure \(\PageIndex{3}\): Explanation of the Bonding in BeH2 Using sp Hybrid Orbitals. Each singly occupied sp hybrid orbital on beryllium can form an electron-pair bond with the singly occupied 1s orbital of a hydrogen atom. Because the two sp hybrid orbitals are oriented at a 180° angle, the BeH2 molecule is linear.
Because both promotion and hybridization require an input of energy, the formation of a set of singly occupied hybrid atomic orbitals is energetically uphill. The overall process of forming a compound with hybrid orbitals will be energetically favorable only if the amount of energy released by the formation of covalent bonds is greater than the amount of energy used to form the hybrid orbitals (Figure \(\PageIndex{4}\)). As we will see, some compounds are highly unstable or do not exist because the amount of energy required to form hybrid orbitals is greater than the amount of energy that would be released by the formation of additional bonds.
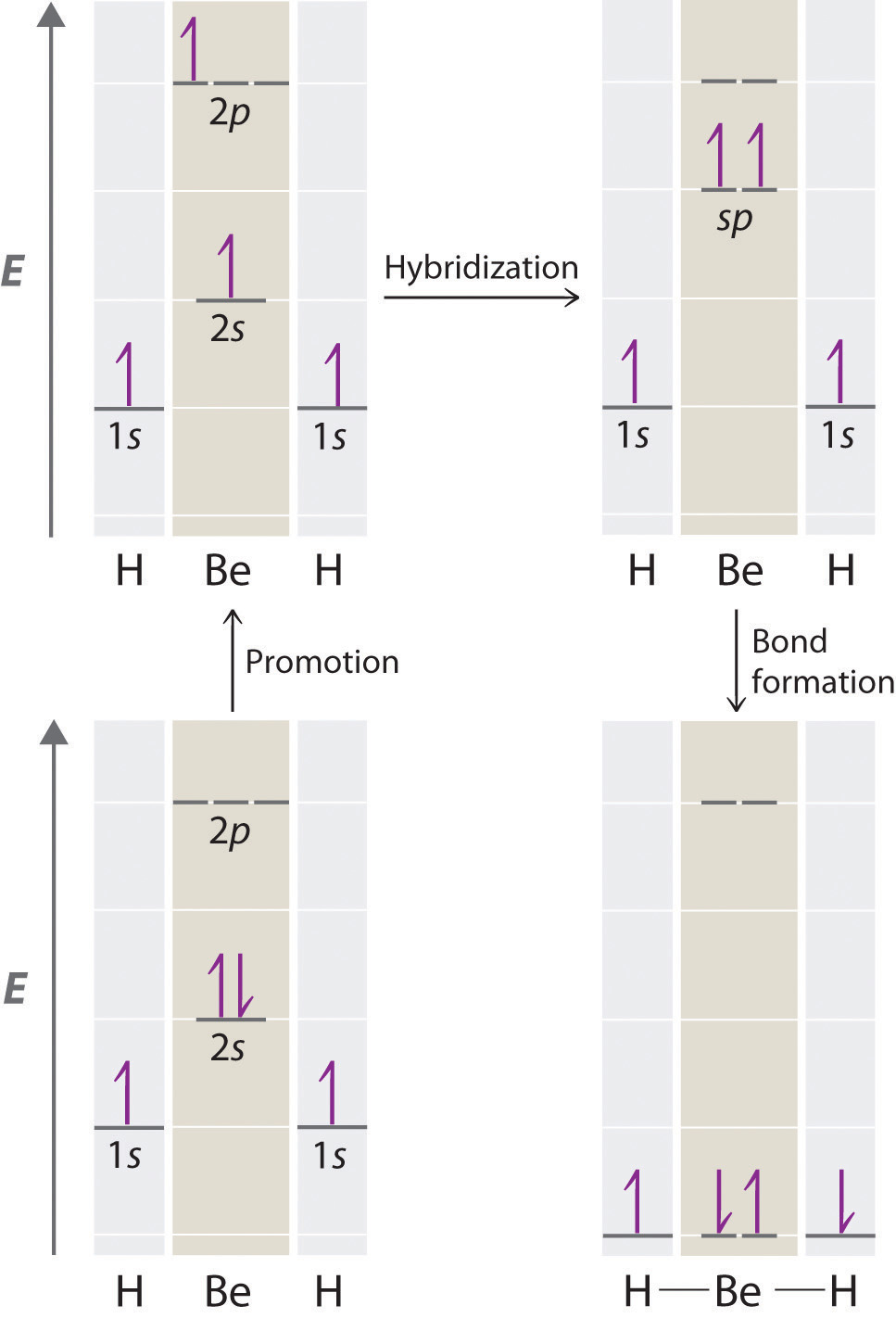
Figure \(\PageIndex{4}\): A Hypothetical Stepwise Process for the Formation of BeH2 from a Gaseous Be Atom and Two Gaseous H Atoms. The promotion of an electron from the 2s orbital of beryllium to one of the 2p orbitals is energetically uphill. The overall process of forming a BeH2 molecule from a Be atom and two H atoms will therefore be energetically favorable only if the amount of energy released by the formation of the two Be–H bonds is greater than the amount of energy required for promotion and hybridization.
The concept of hybridization also explains why boron, with a 2s22p1 valence electron configuration, forms three bonds with fluorine to produce BF3, as predicted by the Lewis and VSEPR approaches. With only a single unpaired electron in its ground state, boron should form only a single covalent bond. By the promotion of one of its 2s electrons to an unoccupied 2p orbital, however, followed by the hybridization of the three singly occupied orbitals (the 2s and two 2p orbitals), boron acquires a set of three equivalent hybrid orbitals with one electron each, as shown here:

The hybrid orbitals are degenerate and are oriented at 120° angles to each other (Figure \(\PageIndex{5}\)). Because the hybrid atomic orbitals are formed from one s and two p orbitals, boron is said to be sp2 hybridized (pronounced “s-p-two” or “s-p-squared”). The singly occupied sp2 hybrid atomic orbitals can overlap with the singly occupied orbitals on each of the three F atoms to form a trigonal planar structure with three energetically equivalent B–F bonds.
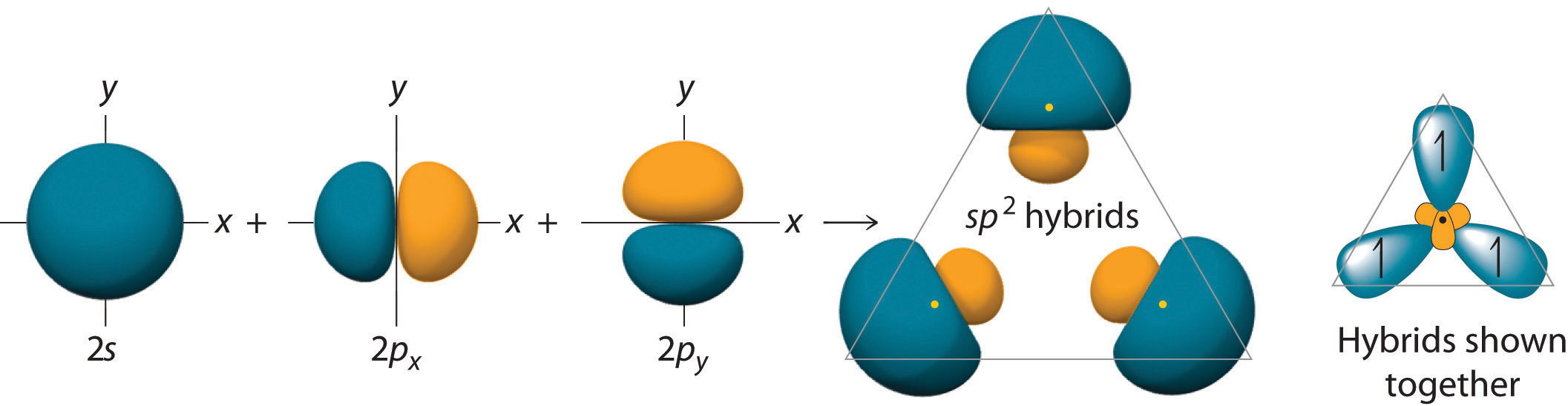
Figure \(\PageIndex{5}\): Formation of sp2 Hybrid Orbitals. Combining one ns and two np atomic orbitals gives three equivalent sp2 hybrid orbitals in a trigonal planar arrangement; that is, oriented at 120° to one another.
Looking at the 2s22p2 valence electron configuration of carbon, we might expect carbon to use its two unpaired 2p electrons to form compounds with only two covalent bonds. We know, however, that carbon typically forms compounds with four covalent bonds. We can explain this apparent discrepancy by the hybridization of the 2s orbital and the three 2p orbitals on carbon to give a set of four degenerate sp3 (“s-p-three” or “s-p-cubed”) hybrid orbitals, each with a single electron:

The large lobes of the hybridized orbitals are oriented toward the vertices of a tetrahedron, with 109.5° angles between them (Figure \(\PageIndex{6}\)). Like all the hybridized orbitals discussed earlier, the sp3 hybrid atomic orbitals are predicted to be equal in energy. Thus, methane (CH4) is a tetrahedral molecule with four equivalent C-H bonds.
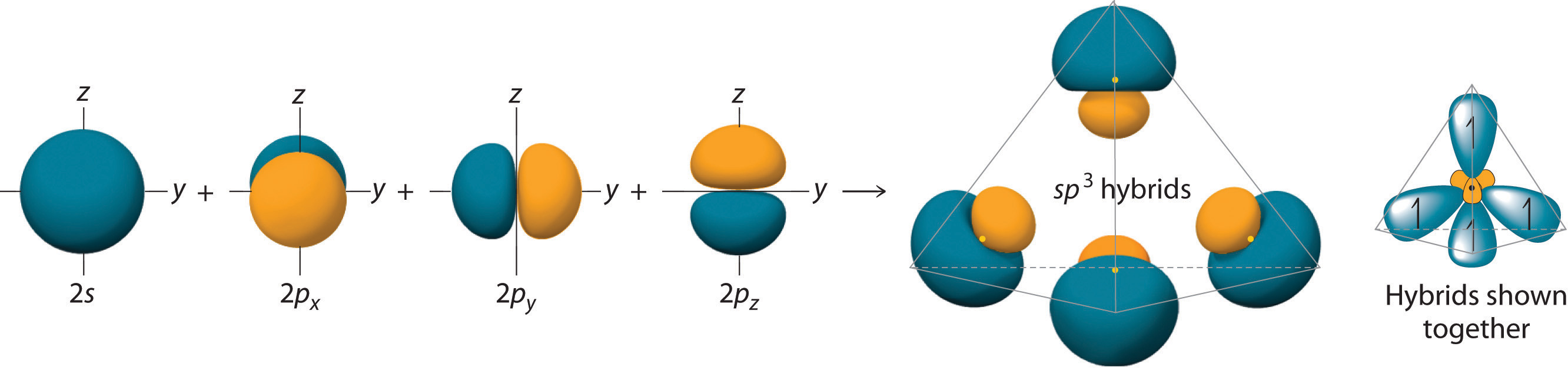
Figure \(\PageIndex{6}\): Formation of sp3 Hybrid Orbitals. Combining one ns and three np atomic orbitals results in four sp3 hybrid orbitals oriented at 109.5° to one another in a tetrahedral arrangement.
In addition to explaining why some elements form more bonds than would be expected based on their valence electron configurations, and why the bonds formed are equal in energy, valence bond theory explains why these compounds are so stable: the amount of energy released increases with the number of bonds formed. In the case of carbon, for example, much more energy is released in the formation of four bonds than two, so compounds of carbon with four bonds tend to be more stable than those with only two. Carbon does form compounds with only two covalent bonds (such as CH2 or CF2), but these species are highly reactive, unstable intermediates that only form in certain chemical reactions.
Valence bond theory explains the number of bonds formed in a compound and the relative bond strengths.
The bonding in molecules such as NH3 or H2O, which have lone pairs on the central atom, can also be described in terms of hybrid atomic orbitals. In NH3, for example, N, with a 2s22p3 valence electron configuration, can hybridize its 2s and 2p orbitals to produce four sp3 hybrid orbitals. Placing five valence electrons in the four hybrid orbitals, we obtain three that are singly occupied and one with a pair of electrons:

The three singly occupied sp3 lobes can form bonds with three H atoms, while the fourth orbital accommodates the lone pair of electrons. Similarly, H2O has an sp3 hybridized oxygen atom that uses two singly occupied sp3 lobes to bond to two H atoms, and two to accommodate the two lone pairs predicted by the VSEPR model. Such descriptions explain the approximately tetrahedral distribution of electron pairs on the central atom in NH3 and H2O. Unfortunately, however, recent experimental evidence indicates that in NH3 and H2O, the hybridized orbitals are not entirely equivalent in energy, making this bonding model an active area of research.
Example \(\PageIndex{1}\)
Use the VSEPR model to predict the number of electron pairs and molecular geometry in each compound and then describe the hybridization and bonding of all atoms except hydrogen.
- H2S
- CHCl3
Given: two chemical compounds
Asked for: number of electron pairs and molecular geometry, hybridization, and bonding
Strategy:
- Using the VSEPR approach to determine the number of electron pairs and the molecular geometry of the molecule.
- From the valence electron configuration of the central atom, predict the number and type of hybrid orbitals that can be produced. Fill these hybrid orbitals with the total number of valence electrons around the central atom and describe the hybridization.
Solution:
- A H2S has four electron pairs around the sulfur atom with two bonded atoms, so the VSEPR model predicts a molecular geometry that is bent, or V shaped. B Sulfur has a 3s23p4 valence electron configuration with six electrons, but by hybridizing its 3s and 3p orbitals, it can produce four sp3 hybrids. If the six valence electrons are placed in these orbitals, two have electron pairs and two are singly occupied. The two sp3 hybrid orbitals that are singly occupied are used to form S–H bonds, whereas the other two have lone pairs of electrons. Together, the four sp3 hybrid orbitals produce an approximately tetrahedral arrangement of electron pairs, which agrees with the molecular geometry predicted by the VSEPR model.
- A The CHCl3 molecule has four valence electrons around the central atom. In the VSEPR model, the carbon atom has four electron pairs, and the molecular geometry is tetrahedral. B Carbon has a 2s22p2 valence electron configuration. By hybridizing its 2s and 2p orbitals, it can form four sp3 hybridized orbitals that are equal in energy. Eight electrons around the central atom (four from C, one from H, and one from each of the three Cl atoms) fill three sp3 hybrid orbitals to form C–Cl bonds, and one forms a C–H bond. Similarly, the Cl atoms, with seven electrons each in their 3s and 3p valence subshells, can be viewed as sp3 hybridized. Each Cl atom uses a singly occupied sp3 hybrid orbital to form a C–Cl bond and three hybrid orbitals to accommodate lone pairs.
Exercise \(\PageIndex{1}\)
Use the VSEPR model to predict the number of electron pairs and molecular geometry in each compound and then describe the hybridization and bonding of all atoms except hydrogen.
- the BF4− ion
- hydrazine (H2N–NH2)
- Answer a
-
B is sp3 hybridized; F is also sp3 hybridized so it can accommodate one B–F bond and three lone pairs. The molecular geometry is tetrahedral.
- Answer b
-
Each N atom is sp3 hybridized and uses one sp3 hybrid orbital to form the N–N bond, two to form N–H bonds, and one to accommodate a lone pair. The molecular geometry about each N is trigonal pyramidal.
In the hybridization model, the number of hybrid orbitals used by the central atom is the same as the number of electron groups around the central atom. Thus,
- 2 electron groups (linear) = sp hybridization
- 3 electron groups (trigonal planar) = sp2 hybridization
- 4 electron groups (tetrahedral) = sp3 hybridization
What about hypervalent molecules, with more than 4 electron groups around the central atom? In the past, the hybridization model has been extended to hypervalent molecules by invoking the participation of d orbitals, with designations such as sp3d for trigonal bipyramidal and sp3d2 for octahedral molecules. However, modern chemical calculations have largely discredited this description by showing that d orbitals do not participate significantly in the bonding of hypervalent molecules. Like all models of chemical bonding, the hybridization model is only useful within its proper limits.
The hybridization model is most useful for describing molecules with only linear, trigonal planar, and tetrahedral centers, such as most organic and biological molecules.
Summary
Hybridization increases the overlap of bonding orbitals and explains the molecular geometries of many species whose geometry cannot be explained using a VSEPR approach. The localized bonding model (called valence bond theory) assumes that covalent bonds are formed when atomic orbitals overlap and that the strength of a covalent bond is proportional to the amount of overlap. It also assumes that atoms use combinations of atomic orbitals (hybrids) to maximize the overlap with adjacent atoms. The formation of hybrid atomic orbitals can be viewed as occurring via promotion of an electron from a filled ns2 subshell to an empty np valence orbital, followed by hybridization, the combination of the orbitals to give a new set of (usually) equivalent orbitals that are oriented properly to form bonds. The combination of an ns and an np orbital gives rise to two equivalent sp hybrids oriented at 180°, whereas the combination of an ns and two or three np orbitals produces three equivalent sp2 hybrids or four equivalent sp3 hybrids, respectively.

