Certain metal ions frequently display distortions from ideal geometry, such that the symmetry of the compound is lowered. In tetragonal distortions of octahedral complexes, for example, the metal-ligand bond distances of two axial ligands may be significantly longer than the distances of the equatorial ligands. Alternatively, two of the metal-ligand distances may be compressed compared to others.
Sometimes, these distortions can be experimentally observed. For example, EXAFS (X-ray absorption fine structure) data for [Cu(OH2)6](BrO3)2, an octahedral complex in which all six Cu-O bonds ought to be the same length, show two different Cu-O distances of 1.96(1) and 2.32(2) Å (the digit in parentheses is used to convey the degree of uncertainty in X-ray measurements).1 That's an approximately 20% difference between the same kind of metal-ligand bond distances within the same complex.
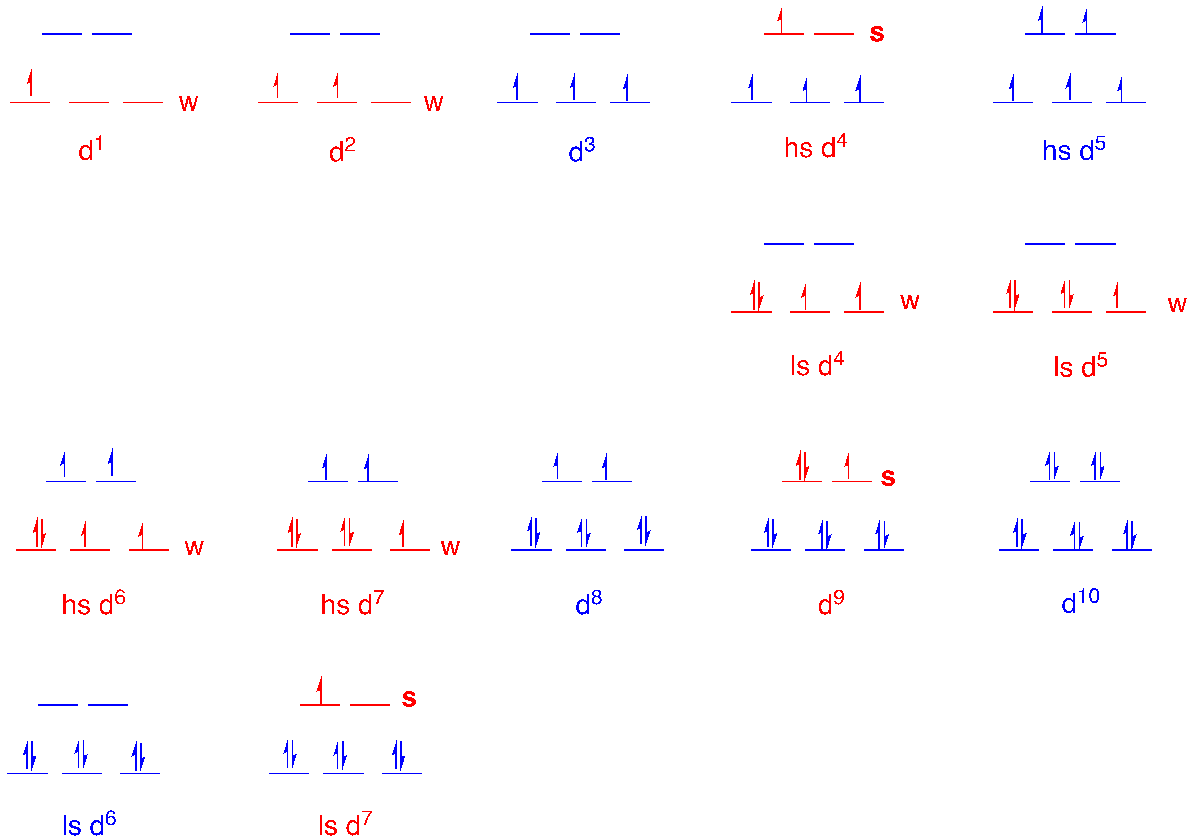
These distortions, often called Jahn-Teller distortions, are observed in complexes of transition metals with specific electron configurations: high spin d4, low spin d7, and d9 (for which there is neither a low nor high spin case). These configurations give rise to unequally occupied degenerate orbitals. Degenerate orbitals are multiple orbitals at the same energy. The three p orbitals in an atomic shell are degenerate, for example. In contrast, non-degenerate orbitals occur at different energy levels. These two cases are illustrated below with the simplest conceivable case, a pair of orbitals.

A set of degenerate orbitals might be equally or unequally occupied depending on the number of available electrons. For example, in the simple case of two degenerate orbitals, equal occupancy would occur if there were two electrons or four electrons because those even numbers of electrons could be divided evenly between the two orbitals. Either one or three electrons would lead to unequally occupied orbitals; there is no way to put the same number of electrons in each orbital in this case.
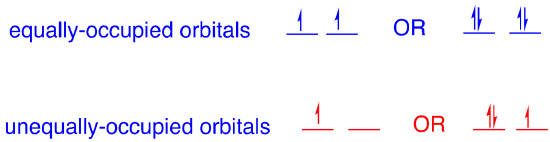
These cases of unequally occupied degenerate orbitals can lead to opportunities for distortion. When the symmetry of a complex drops, two otherwise degenerate orbitals might no longer exist at the same energy as each other. That means, for example, that instead of having three electrons at the same energy, we would have two electrons at lower energy and one at higher. There would be a net decrease in energy in the non-symmetric, distorted case.

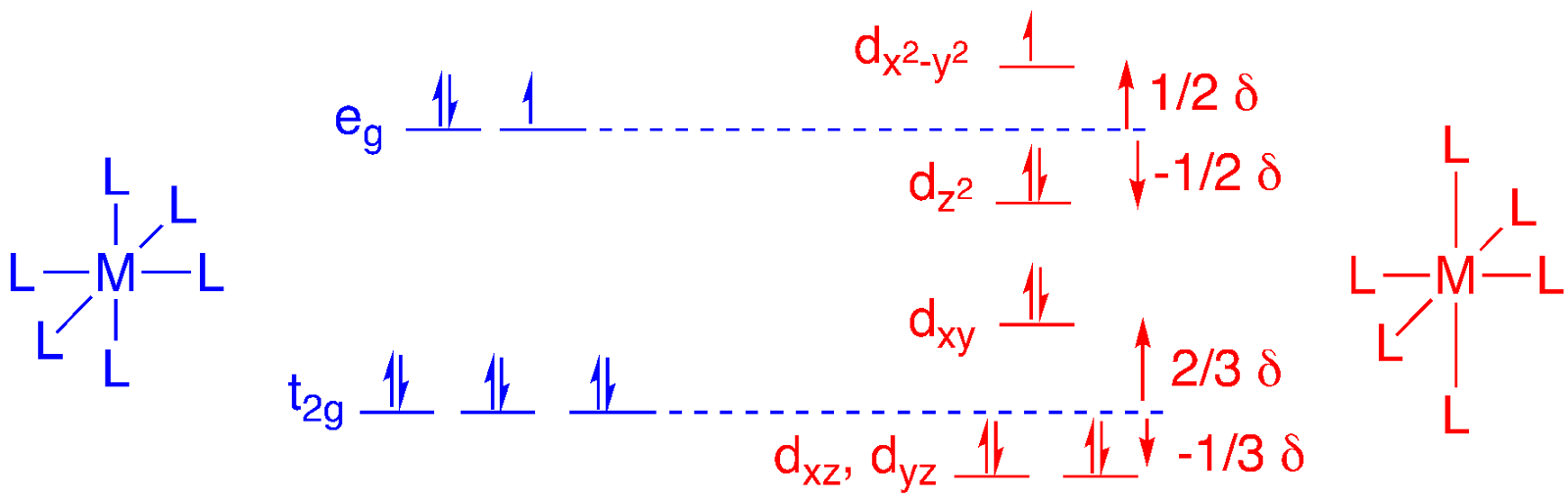
In the context of an octahedral d9 complex, elongation of the bonds to the axial ligands leads to a very slight lowering of the d orbitals that interact with ligands along the z axis: the dz2 and the dxz and dyz. The other orbitals are shown increasing slightly according to the principle that the average energy of the orbitals is preserved at the orbital barycenter (as opposed to the energy of the electrons, which decreases in this case).
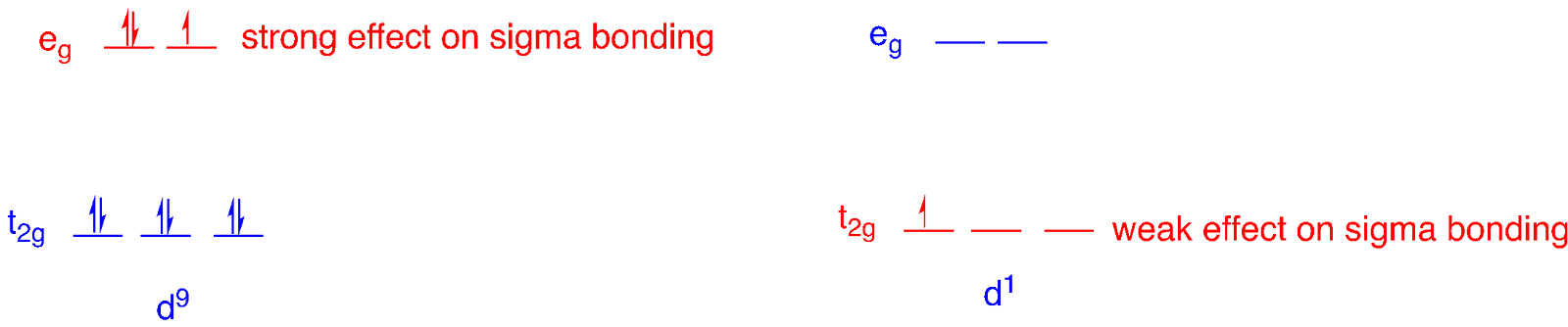
Not all cases of unequally occupied degenerate orbitals produce measurable Jahn Teller distortions. In octahedral geometry, examples of strong Jahn Teller effects are seen when the unequally occupied orbitals are in the eg set rather than the t2g set. The eg set is the one that is linked to sigma bonding, after all, so the orbitals in that level are strongly influenced by the strength of that sigma bonding interaction, and hence the bond length.
Changes in bond length are not the only observable result of the Jahn Teller effect. The absorption spectra of some octahedral complexes show two distinct d-d bands rather than the one band absorbed for pure octahedral symmetry. This observation is a consequence of having additional orbital levels giving rise to distinct electronic transitions. This phenomenon is also seen if the excited state, rather than the ground state, experiences Jahn Teller distortion.
The Jahn Teller effect also plays a role in reactivity. For example, it is thought to promote the lability of octahedral Cu(II) complexes by weakening the bonds to axial ligands via the tetragonal distortion.
References
1. Persson, I.; Persson, P.; Sandstrom, M.; Ullström, A.-S. "Structure of Jahn–Teller distorted solvated copper(ii) ions in solution, and in solids with apparently regular octahedral coordination geometry." J. Chem. Soc. Dalton 2002, 1256-1265.
Problems
1. Given the effect of axial bond elongation on the d orbital energy levels in an octahedral complex, show the corresponding effects that would result from shortening of the axial metal ligand bonds.
2. Fill in octahedral d orbital splitting diagrams for d1 to d10 configurations to show why only high spin d4, low spin d7 and d9 configurations exhibit strong Jahn Teller distortions.
Solutions
1. This time, dz2 is elevated, along with the dxz and dyx.

2. The w indicates a weak Jahn Teller effect. The s indicates a strong Jahn Teller effect.