Homonuclear Correlations
- Page ID
- 1807
Homonuclear 2D J-resolved
This sequence allows to get the coupling constant along the Fl axis and the chemical shift of each uncoupled proton along the F2 axis (Spectrum 1 and 2). Of course, the couplings involving two different nuclei (3IP, 19P coupled to 1H) are always found in the F2 dimension. One can thus determine the coupling between a proton within a multiplet of a coupled spectrum and phosphorus (8). For the 2D J-resolved sequence (Fig. 12), the pulse sequence used is a spin echo sequence. In our example we studied the saccharose molecule (Fig. 29). As in any "echo" experiment, the evolution period tl is divided into two equivalent parts. After the first impulsion of (90°)x, all the magnetization vectors begin to precess as a function of their chemical shifts and the coupling constants. The impulsion of (180°) on the y axis allows for each refocused spin to reassociate the vectors with their chemical shifts.
![fig12[1].jpg](https://chem.libretexts.org/@api/deki/files/15336/fig12%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=160)
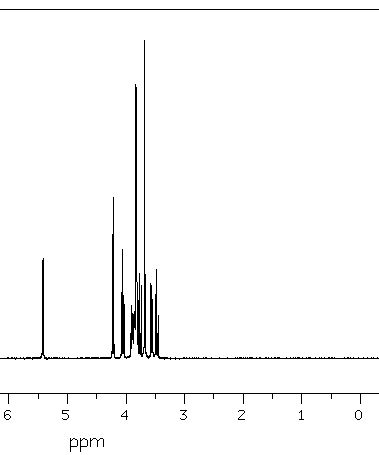
Spectrum 1: 1D proton saccharin.
![fig29[1].jpg](https://chem.libretexts.org/@api/deki/files/15339/fig29%255B1%255D.jpg?revision=1&size=bestfit&width=630&height=210)
![spectre2[1].jpg](https://chem.libretexts.org/@api/deki/files/15337/spectre2%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=427)
Spectrum 2: J-resolved 2D.
The doublet which is located at 4.22 ppm, shows that the f3 proton has a neighboring proton. The coupling constant is directly seen on the F2 axis. The triplet f4 at 4.05 ppm shows that this one has two protons which are closed to him ... (and so on).
The COSY 90 pulse sequence (Correlated SpectroscopY)
The example under study is the saccharine (Fig. 29). The aim of this sequence is to correlate signals of identical nuclei with a scalar coupling. For an isolated nucleus, it is made of two ![chapitre3_1_2_en[1].png](https://chem.libretexts.org/@api/deki/files/15341/chapitre3_1_2_en%255B1%255D.png?revision=1&size=bestfit&width=43&height=16) impulsions on both side of the evolution period t1 (Fig. 13).
impulsions on both side of the evolution period t1 (Fig. 13).
The preparation begins with a relaxation delay allowing the magnetization to come back to its equilibrium, then the period t1 occurs with a stepwise increase and finally the t2 period is the acquisition time (8).
![fig13[1].jpg](https://chem.libretexts.org/@api/deki/files/15342/fig13%255B1%255D.jpg?revision=1&size=bestfit&width=403&height=152)
Following the double Fourier transform, we get a spectrum in chemical shift on the two axis. Moreover, the cross peaks indicate the nuclei which are coupled within each other and allow then a direct attribution of the neighboring protons.
We can understand the obtention of the diagonal and crossing signals of the COSY spectrum by the merely means of quantitative consideration. (8)
In fact, if we consider a singlet signal without scalar spin-spin coupling, the preparation allows to set the maximal amount of nuclei at their right position and the first impulsion ![chapitre3_1_2_en[1].png](https://chem.libretexts.org/@api/deki/files/15341/chapitre3_1_2_en%255B1%255D.png?revision=1&size=bestfit&width=43&height=16) generates a transverse magnetization M(A) which rotates around the Y axis (Fig. 14).
generates a transverse magnetization M(A) which rotates around the Y axis (Fig. 14).
![fig14[1].jpg](https://chem.libretexts.org/@api/deki/files/15343/fig14%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=240)
Fig. 14: After the first impulsion ![chapitre3_1_2_en[1].png](https://chem.libretexts.org/@api/deki/files/15341/chapitre3_1_2_en%255B1%255D.png?revision=1&size=bestfit&width=43&height=16)
During the evolution period, the aimantation M(A) precesses with the frequency of the corresponding nucleus resonance ![chapitre3_1_2_en_2[1].png](https://chem.libretexts.org/@api/deki/files/15344/chapitre3_1_2_en_2%255B1%255D.png?revision=1&size=bestfit&width=59&height=13) in the rotating frame; there is thus a sharing of the spins between the x axis and the y axis (Fig. 15).
in the rotating frame; there is thus a sharing of the spins between the x axis and the y axis (Fig. 15).
![fig15[1].jpg](https://chem.libretexts.org/@api/deki/files/15345/fig15%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=240)
The components Mx and My of the transverse magnetization at the end of the evolution period in the Ox and Oy axis of the rotating frame are then:
![chapitre3_1_2_en_3[1].png](https://chem.libretexts.org/@api/deki/files/15346/chapitre3_1_2_en_3%255B1%255D.png?revision=1&size=bestfit&width=224&height=16)
![chapitre3_1_2_en_4[1].png](https://chem.libretexts.org/@api/deki/files/15347/chapitre3_1_2_en_4%255B1%255D.png?revision=1&size=bestfit&width=226&height=18)
Where M0 is the aimantation contribution before the execution of the first impulsion and T2* the apparent transverse relaxation time of the corresponding nucleus.
The second impulsion ![chapitre3_1_2_en_1[1].png](https://chem.libretexts.org/@api/deki/files/15348/chapitre3_1_2_en_1%255B1%255D.png?revision=1&size=bestfit&width=26&height=15) allows to rotate the y component which stays in the xy plane, in the negative z part direction (-z). These last one will not be detected (Fig. 16). However, the x part, still in the xy plane will be taken into account.
allows to rotate the y component which stays in the xy plane, in the negative z part direction (-z). These last one will not be detected (Fig. 16). However, the x part, still in the xy plane will be taken into account.
![fig16[1].jpg](https://chem.libretexts.org/@api/deki/files/15349/fig16%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=240)
![chapitre3_1_2_en_1[1].png](https://chem.libretexts.org/@api/deki/files/15348/chapitre3_1_2_en_1%255B1%255D.png?revision=1&size=bestfit&width=26&height=15) x
xThe magnetization which is going to be detected is of the form: ![chapitre3_1_2_en_7[1].png](https://chem.libretexts.org/@api/deki/files/15350/chapitre3_1_2_en_7%255B1%255D.png?revision=1&size=bestfit&width=81&height=16) , where as the magnetization along the –z axis followed the formula:
, where as the magnetization along the –z axis followed the formula: ![chapitre3_1_2_en_8[1].png](https://chem.libretexts.org/@api/deki/files/15351/chapitre3_1_2_en_8%255B1%255D.png?revision=1&size=bestfit&width=77&height=15) .
.
The intensity of the signal to be recorded depends thus of the time dependent position of the M(A) vector at the very time of the end of the evolution period. This intensity is determined by the Larmor frequency of the A nucleus. The amplitude is modulated in t1 versus this frequency and the Fourier transform yields in both dimensions the frequency ![chapitre3_1_2_en_9[1].png](https://chem.libretexts.org/@api/deki/files/15352/chapitre3_1_2_en_9%255B1%255D.png?revision=1&size=bestfit&width=16&height=11) and then a diagonal signal. In the case of a spin-spin coupling, the second impulsion
and then a diagonal signal. In the case of a spin-spin coupling, the second impulsion ![chapitre3_1_2_en_1[1].png](https://chem.libretexts.org/@api/deki/files/15348/chapitre3_1_2_en_1%255B1%255D.png?revision=1&size=bestfit&width=26&height=15) does not only induce a change in the transverse A magnetization, but also changes of populations for other transitions in the spin system under study. Therefore, an exchange of magnetization occurs between all the nuclei which are coupled between each other. Their signals, in a set of experiments t1, are in the same way modulated versus the neighboring nuclei.
does not only induce a change in the transverse A magnetization, but also changes of populations for other transitions in the spin system under study. Therefore, an exchange of magnetization occurs between all the nuclei which are coupled between each other. Their signals, in a set of experiments t1, are in the same way modulated versus the neighboring nuclei.
This ends up with cross peaks of the 2D spectrum in ![chapitre3_1_2_en_11[1].png](https://chem.libretexts.org/@api/deki/files/15353/chapitre3_1_2_en_11%255B1%255D.png?revision=1&size=bestfit&width=54&height=15) and
and ![chapitre3_1_2_en_12[1].png](https://chem.libretexts.org/@api/deki/files/15354/chapitre3_1_2_en_12%255B1%255D.png?revision=1&size=bestfit&width=54&height=15) and allows us to get a spectrum in which the homonuclear scalar coupling constants are figure out by spots outside of the diagonal.
and allows us to get a spectrum in which the homonuclear scalar coupling constants are figure out by spots outside of the diagonal.
For example, we might see the coupling between the f3 and f4 protons at the crossing of 4.05 and 4.18 ppm (Spectrum 3).
![spectre3[1].jpg](https://chem.libretexts.org/@api/deki/files/15355/spectre3%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=427)
Spectrum 3: COSY 90° Both impulsions are at 90°.
The COSY 45 pulse sequence
The example is given for the saccharose (Fig. 29). The second impulsion is of 45°. The drawback of this second pulse is to diminish the signal to noise ratio (Fig 17). However it allows a more easy attribution of the signals of the spectrum in the cases of strong AB type coupling. In fact, the correlations spots near the diagonal are no more susceptible to be hidden by the auto correlation peaks (Spectrum 4).
![spectre4[1].jpg](https://chem.libretexts.org/@api/deki/files/15356/spectre4%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=427)
Spectrum 4: COSY 45°. We observe a strong diminution of the autocorrelation peaks.
![fig17[1].jpg](https://chem.libretexts.org/@api/deki/files/15357/fig17%255B1%255D.jpg?revision=1&size=bestfit&width=316&height=630)
The long range coupling: COSY
This experiment allows the detection of the correlation peaks caused by weak coupling constant (less than one Hz) and which are not detectable with the COSY 9O° pulse sequence (8).
For the "long range" COSY sequence, we artificially increase the evolution and detection period by introducing a fixed ![chapitre3_1_4_en[1].png](https://chem.libretexts.org/@api/deki/files/15358/chapitre3_1_4_en%255B1%255D.png?revision=1&size=bestfit&width=11&height=12) delay on both side of the mixing time (Fig. 18).
delay on both side of the mixing time (Fig. 18).
![fig18[1].jpg](https://chem.libretexts.org/@api/deki/files/15359/fig18%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=160)
The chosen example is the saccharine molecule (see also Fig 29).
The spectrum 5 is a 90° COSY pulse sequence: The scalar coupling between neighboring protons G1 and G2 are clearly seen. The spectrum 6 is a L.R. COSY pulse sequence.:The long range couplings appear between the G1 proton and the G3 and G4 protons.
![spectre5[1].jpg](https://chem.libretexts.org/@api/deki/files/15360/spectre5%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=427)
Spectrum 5: 90° COSY
![spectre6[1].jpg](https://chem.libretexts.org/@api/deki/files/15361/spectre6%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=427)
Spectrum 6: LR COSY
The relayed COSY or one homonuclear step relayed COSY
A COSY spectrum may sometimes be inefficient to clearly identify all the signals, particularly if per chance two nuclei are equivalent. A typical example is that of peptides (Fig 19) where protons born by ![chapitre3_1_5_en[1].png](https://chem.libretexts.org/@api/deki/files/15362/chapitre3_1_5_en%255B1%255D.png?revision=1&size=bestfit&width=10&height=9) carbon of different amino acids have closed chemical shifts; the COSY spectrum gives informations of the correlations between
carbon of different amino acids have closed chemical shifts; the COSY spectrum gives informations of the correlations between ![chapitre3_1_5_en[1].png](https://chem.libretexts.org/@api/deki/files/15362/chapitre3_1_5_en%255B1%255D.png?revision=1&size=bestfit&width=10&height=9) proton and
proton and ![chapitre3_1_5_en_2[1].png](https://chem.libretexts.org/@api/deki/files/15363/chapitre3_1_5_en_2%255B1%255D.png?revision=1&size=bestfit&width=11&height=16) protons in one hand and between
protons in one hand and between ![chapitre3_1_5_en[1].png](https://chem.libretexts.org/@api/deki/files/15362/chapitre3_1_5_en%255B1%255D.png?revision=1&size=bestfit&width=10&height=9) protons and NH protons on the other hand. Unfortunately, due to the overlapping of the
protons and NH protons on the other hand. Unfortunately, due to the overlapping of the ![chapitre3_1_5_en[1].png](https://chem.libretexts.org/@api/deki/files/15362/chapitre3_1_5_en%255B1%255D.png?revision=1&size=bestfit&width=10&height=9) protons signals, the attribution for the
protons signals, the attribution for the ![chapitre3_1_5_en_2[1].png](https://chem.libretexts.org/@api/deki/files/15363/chapitre3_1_5_en_2%255B1%255D.png?revision=1&size=bestfit&width=11&height=16) protons signals can not be deduced from the NH protons (or the other way around). To solve this problem, we should be able to correlate the NH proton signals to those of the
protons signals can not be deduced from the NH protons (or the other way around). To solve this problem, we should be able to correlate the NH proton signals to those of the ![chapitre3_1_5_en_2[1].png](https://chem.libretexts.org/@api/deki/files/15363/chapitre3_1_5_en_2%255B1%255D.png?revision=1&size=bestfit&width=11&height=16) protons; such a correlation may be obtained either by a long range COSY if the 4J coupling is not too weak or, better, by a relayed COSY experiment which allows the correlation of the signal from two nuclei at the only requirement that both of them are coupled to a third one (8).
protons; such a correlation may be obtained either by a long range COSY if the 4J coupling is not too weak or, better, by a relayed COSY experiment which allows the correlation of the signal from two nuclei at the only requirement that both of them are coupled to a third one (8).
![fig19[1].jpg](https://chem.libretexts.org/@api/deki/files/15364/fig19%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=320)
This experiment allows the differentiation of the belonging of the NH versus the ![chapitre3_1_5_en_3[1].png](https://chem.libretexts.org/@api/deki/files/15365/chapitre3_1_5_en_3%255B1%255D.png?revision=1&size=bestfit&width=39&height=18) or
or ![chapitre3_1_5_en_4[1].png](https://chem.libretexts.org/@api/deki/files/15366/chapitre3_1_5_en_4%255B1%255D.png?revision=1&size=bestfit&width=41&height=18) .
.
It is widely used for the sugar structure determination. The pulse sequence of the experiment is derived from the COSY sequence in which the mixing pulse is followed by a fixed time ![chapitre3_1_5_en_5[1].png](https://chem.libretexts.org/@api/deki/files/15367/chapitre3_1_5_en_5%255B1%255D.png?revision=1&size=bestfit&width=8&height=9) and by a 90° pulse (Fig. 20).
and by a 90° pulse (Fig. 20).
A 180° pulse, achieved in the middle of the new mixing period is also needed for the elimination of the evolution of the magnetization (refocalization) due to the chemical shifts during this additional delay.
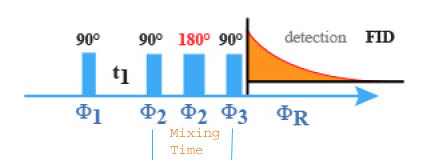
Applied to the AMX type system, this pulse sequence achieves a first coherence transfer from A to M as that one observed in the COSY experiment. During the mixing time, the magnetization evolve in such a wav that ideally the different components of the magnetization of the M nucleus are in anti phase versus the JMX coupling. The third impulsion at 90° achieves then the transfer from the M nucleus toward the X nucleus. The phase cycles of the impulsions and of the receiver is derived from that of the COSY experiment. However, it needs an additional base cycle for the elimination of the artifacts due to transfers of the NOESY type. This consists to inverse the phase of the second impulsion without modifying the reception phase. The result is a global cycle with 8 components:
![chapitre3_1_5_en_7[1].png](https://chem.libretexts.org/@api/deki/files/15369/chapitre3_1_5_en_7%255B1%255D.png?revision=1&size=bestfit&width=20&height=12) = 0,
= 0, ![chapitre3_1_5_en_8[1].png](https://chem.libretexts.org/@api/deki/files/15370/chapitre3_1_5_en_8%255B1%255D.png?revision=1&size=bestfit&width=22&height=12) = 0 0 1 1 2 2 3 3 ,
= 0 0 1 1 2 2 3 3 , ![chapitre3_1_5_en_9[1].png](https://chem.libretexts.org/@api/deki/files/15371/chapitre3_1_5_en_9%255B1%255D.png?revision=1&size=bestfit&width=21&height=13) = 0 2 1 3,
= 0 2 1 3, ![chapitre3_1_5_en_10[1].png](https://chem.libretexts.org/@api/deki/files/15372/chapitre3_1_5_en_10%255B1%255D.png?revision=1&size=bestfit&width=24&height=12) = 0 0 2 2
= 0 0 2 2
For optimizing the mixing time, we have to define the delay ![chapitre3_1_5_en_5[1].png](https://chem.libretexts.org/@api/deki/files/15367/chapitre3_1_5_en_5%255B1%255D.png?revision=1&size=bestfit&width=8&height=9) between each impulsion. This one is deduced from the following formula where Jmax stands for the value of the biggest coupling constant:
between each impulsion. This one is deduced from the following formula where Jmax stands for the value of the biggest coupling constant:
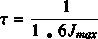
COSY experiment with a double quantum filter (DQF COSY)
The COSY sequence with double quantum filter affords some advantages compared to the conventional cosy (2). The diagonal spots and the correlation spots are not phase shifted to 90° and they have the same anti phase structure (Fig. 21). It is thus possible to phase as a whole all the peaks of the spectrum in positive or in negative absorption allowing thus an easier identification of the peaks whose correlations are the closest to the diagonal. These diagonal peaks correspond to singlet signals and are thus eliminated. Unfortunately the sensitivity is divided by 2.
![fig21[1].jpg](https://chem.libretexts.org/@api/deki/files/15374/fig21%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=160)
The molecule which is used as an example is the saccharine (Fig. 29). We may notice on the spectrum 7 (DQF COSY), a strong decrease of the singlet of the proton F1 which is located at 3.68 ppm compared to the spectrum 3.
![spectre7[1].jpg](https://chem.libretexts.org/@api/deki/files/15375/spectre7%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=427)
Spectrum 7: DQF COSY.
The NOESY sequence (Nuclear Over Hauser Enhancement Spectroscopy)
It introduces the crossed relaxation swhich governs the Over Hauser effect (2). The NOESY spectroscopy is rather limited to the determination of the notion of crossed homonuclear relaxation. The pulse sequence scheme is given Figure 22.
![fig22[1].jpg](https://chem.libretexts.org/@api/deki/files/15376/fig22%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=160)
The correlation spots (peaks outside of the diagonal) indicate either a dipolar interaction, thus a given spatial vicinity (2 to 5 A°) between the spins under study, or a chemical shift. This experiment allows the determination of large molecules such as the proteins.
The spectrum 8 is a COSY 45° of the phenanthro-benzofurane (PBF) (Fig.30). The spectrum 9 is the corresponding NOESY spectrum We observe an additional correlation spot between the proton which is at 8.8 ppm and the proton which has a chemical shift of 8.6 ppm. This spot is termed A, it means a dipolar interaction between two protons H1 and H2.
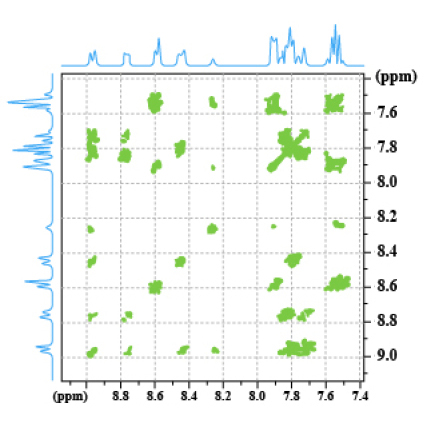
Spectrum 8: COSY spectrum of PBF
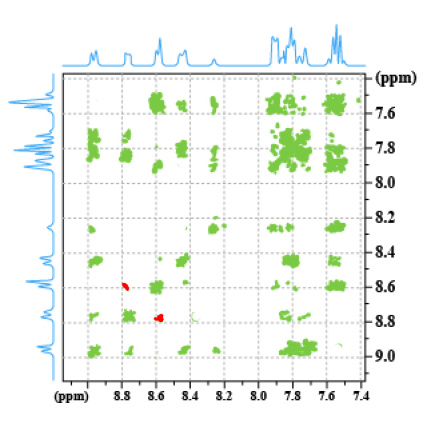
Spectrum 9: NOESY spectrum of PBF
Phase Sensitive COSY and NOESY
The TPPI technique (Time Proportional Phase incremantation) allows detection in a quadratic sequence. We may therefore solve the problem of the discrimination of the sign of the frequencies upon the detection of a free precession signal in an experiment of impulsional NMR There are other methods in the phase mode like the STATES technique where the detection is in simultaneous quadratic. It is easier to achieve a phased NOESY rather than a classical NOESY, because this technique is much more sensitive. Moreover, the correlation spots meaning a spatial vicinity are in the negative portion of the spectrum versus the correlation spots due to the spin-spin coupling. (5)
TOCSY and ROESY
These experiments are characterized by a mixing time during which the magnetization of a spin A, submitted to a radio wave frequency field B1 is transferred to a spin linked to A either by a dipolar coupling or by a scalar coupling. During the mixing time the magnetization is locked according to one direction of the space defined by the direction of the field B1 and the spin frequency shifting versus the main component. The block in the spin system is commonly named spin-lock (2).
TOCSY or HOHAHA
This method allows to demonstrate scalar couplings. The pulse sequence scheme is given Fig. 23. The first 90°x impulsion rotates the magnetization vectors in the xOy plane, in which they freely evolve during the time t1, under the influence of their chemical shift and the scalar coupling constants. We apply then a spin lock on the x axis, that means a low power impulsion or set of impulsions whose duration represents the mixing time tm. During this time, the spin coherence of the system is exchanged. By increasing the mixing time we increase the number of the visible transitions. That is to say that within the same experiment, we get the informations of a COSY, of a LR COSY and of a relayed COSY. The pulse sequence widely used is base upon the MLEV-17 sequence which contains a set of 17 pulses. (5).
![fig23[1].jpg](https://chem.libretexts.org/@api/deki/files/15379/fig23%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=160)
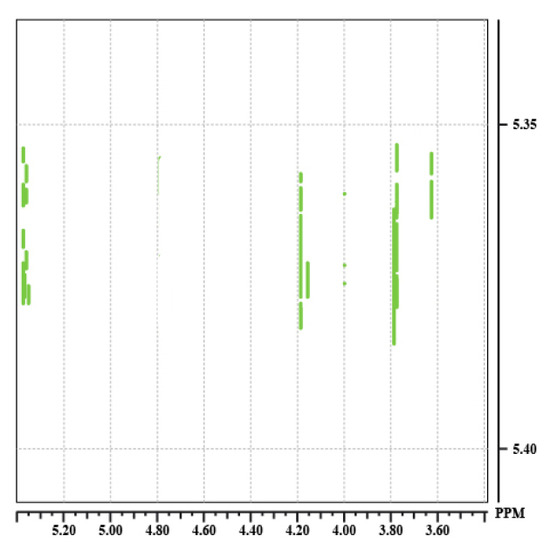
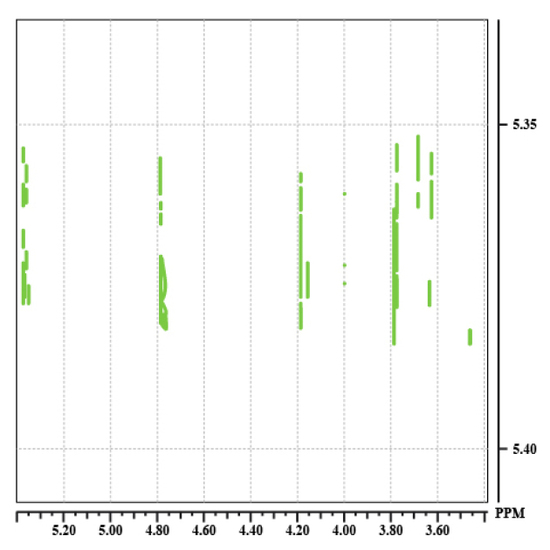
The spectrum 10 shows the result of three different mixing time for the saccharose (Fig. 29). These are given in milliseconds (20, 60, 100 ms). For each mixing time, we see the appearance of new correlation spots. There is thus an increase of the number of relays with the spin lock time. These ones correspond then to long range correlations.
![Tocsy100[1].jpg](https://chem.libretexts.org/@api/deki/files/15382/Tocsy100%255B1%255D.jpg?revision=1&size=bestfit&width=211&height=211)
Spectrum 10: 20 ms, 60 ms, 100 ms.
ROESY and CAMELSPIN
The aim of the dipolar correlation experiments in two dimensions is to take advantage of the vicinity in space of some nuclei. The result of this kind of experiment is a 2D map in which the signals outside of the diagonal arise from the Over Hauser enhancement effect between two space coupled nuclei (2) (Fig. 24).
![fig24[1].jpg](https://chem.libretexts.org/@api/deki/files/15383/fig24%255B1%255D.jpg?revision=1&size=bestfit&width=427&height=160)
In this case, we apply a spin-lock onto the y axis. The correlation peaks arising from the ROE effect are on the opposite sign compared to the diagonal one their intensity is different from 0. However, the correlation peaks coming from a chemical exchange are of the same sign than the crossing one. The ROESY experiment allows by this way the separation of the contributions coming from the exchange and those coming from the dipolar interactions. The ROESY sequence is thus complementary of the NOESY one and it is more often used for the structural determination of the small molecules.

