Free-Electron Model
- Page ID
- 8852
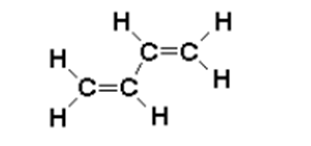
The simple quantum-mechanical problem we have just solved can provide an instructive application to chemistry: the free-electron model (FEM) for delocalized \(\pi\)-electrons. The simplest case is the 1,3-butadiene molecule
\[\rho =2\psi _{1}^2+2\psi _{2}^2\label{28}\]
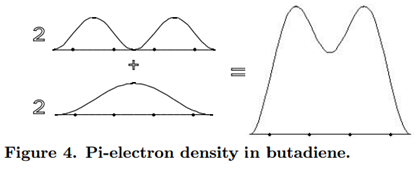
A chemical interpretation of this picture might be that, since the \(\pi\)-electron density is concentrated between carbon atoms 1 and 2, and between 3 and 4, the predominant structure of butadiene has double bonds between these two pairs of atoms. Each double bond consists of a \(\pi\)-bond, in addition to the underlying \(\sigma\)-bond. However, this is not the complete story, because we must also take account of the residual \(\pi\)-electron density between carbons 2 and 3. In the terminology of valence-bond theory, butadiene would be described as a resonance hybrid with the contributing structures CH2=CH-CH=CH2 (the predominant structure) and ºCH2-CH=CH-CH2º (a secondary contribution). The reality of the latter structure is suggested by the ability of butadiene to undergo 1,4-addition reactions.
The free-electron model can also be applied to the electronic spectrum of butadiene and other linear polyenes. The lowest unoccupied molecular orbital (LUMO) in butadiene corresponds to the n=3 particle-in-a-box state. Neglecting electron-electron interaction, the longest-wavelength (lowest-energy) electronic transition should occur from n=2, the highest occupied molecular orbital (HOMO).
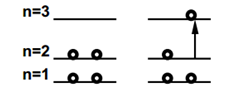
The energy difference is given by
\[\Delta E=E_{3}-E_{2}=(3^2-2^2)\dfrac{h^2}{8mL^2}\label{29}\]
Here m represents the mass of an electron (not a butadiene molecule!), 9.1x10-31 Kg, and L is the effective length of the box, 4x1.40x10-10 m. By the Bohr frequency condition
\[\Delta E=h\upsilon =\dfrac{hc}{\lambda }\label{30}\]
The wavelength is predicted to be 207 nm. This compares well with the experimental maximum of the first electronic absorption band, \(\lambda_{max} \approx\) 210 nm, in the ultraviolet region.
We might therefore be emboldened to apply the model to predict absorption spectra in higher polyenes CH2=(CH-CH=)n-1CH2. For the molecule with 2n carbon atoms (n double bonds), the HOMO → LUMO transition corresponds to n → n + 1, thus
\[\dfrac{hc}{\lambda} \approx \begin{bmatrix}(n+1)^2-n^2\end{bmatrix}\dfrac{h^2}{8m(2nL_{CC})^2}\label{31}\]
A useful constant in this computation is the Compton wavelength
\[\dfrac{h}{mc}= 2.426 \times 10^{-12} m.\]
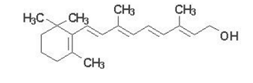
For n=3, hexatriene, the predicted wavelength is 332 nm, while experiment gives \(\lambda _{max}\approx \) 250 nm. For n=4, octatetraene, FEM predicts 460 nm, while \(\lambda _{max}\approx\) 300 nm. Clearly the model has been pushed beyond range of quantitate validity, although the trend of increasing absorption band wavelength with increasing n is correctly predicted. Incidentally, a compound should be colored if its absorption includes any part of the visible range 400-700 nm. Retinol (vitamin A), which contains a polyene chain with n=5, has a pale yellow color. This is its structure:
Contributors and Attributions
Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)

