Critical Point
- Page ID
- 1630
This module refers to a finite amount of particles placed in a closed container (i.e. no volume change) in which boiling cannot occur. The inability for boiling to occur- because the particles in the container are not exposed to the atmosphere, results in the incessant increase of temperature and pressure. The critical point is the temperature and pressure at which the distinction between liquid and gas can no longer be made.
Introduction
At the critical point, the particles in a closed container are thought to be vaporizing at such a rapid rate that the density of liquid and vapor are equal, and thus form a supercritical fluid. As a result of the high rates of change, the surface tension of the liquid eventually disappears. You will have noticed that this liquid-vapor equilibrium curve has a top limit (labeled as C in the phase diagram in Figure 1), which is known as the critical point. The temperature and pressure corresponding to this are known as the critical temperature and critical pressure. If you increase the pressure on a gas (vapor) at a temperature lower than the critical temperature, you will eventually cross the liquid-vapor equilibrium line and the vapor will condense to give a liquid.
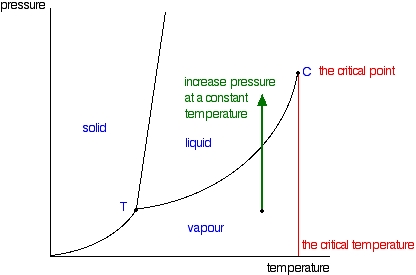
Figure 1: Phase diagram for a single component system with critical point emphasized
This works fine as long as the gas is below the critical temperature. What, though, if your temperature was above the critical temperature? There wouldn't be any line to cross! That is because, above the critical temperature, it is impossible to condense a gas into a liquid just by increasing the pressure. All you get is a highly compressed gas. The particles have too much energy for the intermolecular attractions to hold them together as a liquid. The critical temperature obviously varies from substance to substance and depends on the strength of the attractions between the particles. The stronger the intermolecular attractions, the higher the critical temperature.
Why the Critical Point is Important
The condensation of a gas will never occur above the critical point. A massive amount of pressure can be applied to a gas in a closed container, and it may become highly dense, but will not exhibit a meniscus. Molecules at critical temperatures possess high kinetic energy, and as a result the intermolecular forces in the molecules are weakened.
The Declined Critical Points of Polymer Solutions
A novel discovery made by the University of Manchester, identified that lower critical temperatures are existent in polymer solutions. It has been manifested that hydrocarbon polymers integrated with a hydrocarbon solution portrays what the university terms a "L.C.S.T." or a lower critical solution temperature. This lower critical solution temperature of polymers has been proclaimed to be in a range near the gas- liquid critical point of the polymer's solvent, and can reach up to 170 degrees Celsius. Such a lower critical solution temperature can be contributed to the assimilation of the heat and volume of the substance n-pentane with most hydrocarbon polymers at room temperature (Freeman, P.I., Rowlinson, J.S.).
The Effects of Wetting on the Critical Point
When a fluid is present in two phases, in a container, and a critical point is near establishment, contact with the imminently forming third phase does not occur. This phenomena can be accounted for by examining the other two existing phases; the third phase does not immediately form because one of the other two phases wets the third phase, causing it to be eliminated. This wetting phase will continually occur when a phase is not entirely stable as a whole.
Problems
Temperature and vapor pressure are essential to the stimulation of a critical point; the following problems interconnect the two concepts.
- Determine the vapor pressure of liquid gold at 1936 °C if 200 L of Ne gas is permitted to assimilate with the metal causing it to decline in mass by 0.213 g.
- Approximately 0.423 g H2O is preserved at a temperature of 62 °C in a sealed flask at a volume of 0.726 L. When in equilibrium, will the water be present solely as a liquid?
- Taking into account the previous problem, would it be probable for the sample of water in the flask to be solitarily present as a vapor?
- Is it possible for the the sample of water in problem number two to exist in both the liquid and vapor form at equilibrium?
- The vapor pressure of H2O at 30 °C is 46.2 mmHg. What is the vapor pressure of water at 28 °C, if the enthalpy of fusion is 44 kJ/mol?
Solutions
1. In correlation with Dalton's Law of partial pressure, the gold vapor can be interpreted as a solitary gas occurring at the given volume of Neon. The ideal-gas law will be utilized to determine the vapor pressure.
\[PV=nRT\]
- P=?
- V=200L
- T=1936.C (to convert to K add 273)=2209 K
- R=00820L atm/mol K
Convert to mol the molar mass of Au
\[n= 0.213\; \cancel{g} \left( \dfrac{1 \;mol\; Au}{196.9\; \cancel{g}\; Au}\right) = 0.00108\; mol\; Au\]
\(PV=nRT\) can then be algebraically converted into \(P=\dfrac{nRT}{V}\). Substitute you attained values.
\[P= \dfrac{ (0.00108 \;mol) \times (0.08206\; L \; atm / mol K) \times (2209 \; K)}{ 200 \; L}\]
\[P= 9.78\times 10^{-4}\; atm\]
2. Taking into account the density of water, 1 g/ml, a 0.423 g sample of \(H_2O\) would amount to 0.42 ml. Considering this, it can be concluded that the water in the flask could not solely exist as a liquid at equilibrium since a 0.42 ml sample of water is incapable of accounting for the overall volume present in the flask (0.726L).
3. The ideal gas law can be applied to determine whether or not the water in the flask could solely exist in the vapor form. Rearrange the Ideal Gas Law:
\[P=\dfrac{nRT}{V}\]
- n= (0.423g)*(1 mol/18 g H2O)=0.0235mol
- R=0.08206 L atm/ mol K
- T=62°C + 273 = 335K
- V=0.726 L
\[P= \dfrac{(0.0235 \;mol) \times (0.08206 \;L\; atm/mol\; K) \times (335\; K)}{0.726\; L}\]
\[P=0.889 atm\]
The actual Vapor pressure of water at 60 °C is \(149.4\; mmHg\).
To make a comparison to the vapor pressure attained at 62°C (which is within a close range of the temperature of 60 degrees Celsius), convert the vapor pressure calculated in atm to mmHg.
\[(0.889\;\cancel{atm})* \left(\dfrac{760\;mmHg}{1\; \cancel{atm}}\right)=676.27 \;mmHg\]
Comparing this vapor pressure with the actual vapor pressure of water at 60 °C, it can be concluded that it is improbable that water solely exists in the flask as vapor since this attained vapor pressure exceeds that of the actual vapor pressure that occurs naturally.
4. As the prior explications and calculations have proven, the sample of water is incapable of existing in the flask as either a liquid or vapor alone. Therefore vapor and liquid must exist together at 60 °C and 149.4 mmHg.
5. To evaluate the pressure of water at 28 °C, the Clausius-Clapeyron equation must be used.
\[\ln \dfrac{P_1}{P_2}= \dfrac{H_{vap}}{R} \left( \dfrac{1}{T_2}- \dfrac{1}{T_1} \right)\]
Begin by designating the variables in the equation to the given values in the problem.
If \(T_2 =30 °C\) and \(P_2= 46.2\; mmHg\), what is \(P_1\) when \(T_1=28 °C\)
The units for temperature must be in Kelvin.
- \(T_2= 30 °C + 273.15 K = 303.15\; K\)
- \(T_1 =28 °C\; +273.15 =301.15\; K\)
The enthalpy of vaporization (44 kJ/ mol) should be converted to J/ mol to allow for unit cancelation.
\[44 \;\cancel{kJ}/mol \left(\dfrac{1000\; J}{1\; \cancel{kJ}}\right)= 44.0 \times 10^{3} J/mol.\]
R= 8.3145 J/mol K
Substituting the values in the equation one you obtain:
\[\ln \left(\dfrac{46.2\; mmHg}{P_1}\right) = \dfrac{44,000\; J \;mol^{-1}}{8.3145 \;J/mol\; K} \left(\dfrac{1}{ 301.15 \;K} - \dfrac{1}{ 303.15 \;K}\right)\]
To eliminate the natural logarithm, take the exponentl of both sides:
\[ e^{\ln \left(\dfrac{46.2\; mmHg}{P_1}\right) }= e^{ \dfrac{44,000\; J \;mol^{-1}}{8.3145 \;J/mol\; K} \left(\dfrac{1}{ 301.15 \;K} - \dfrac{1}{ 303.15 \;K}\right)}\]
\[ \dfrac{46.2\; mmHg}{P_1} = e^{ \dfrac{44,000\; J \;mol^{-1}}{8.3145 \;J/mol\; K} \left(\dfrac{1}{ 301.15 \;K} - \dfrac{1}{ 303.15 \;K}\right)}\]
\[\dfrac{46.2\; mmHg}{P_1} = e^{0.11593} \]
\[\dfrac{46.2\; mmHg}{P_1} = 1.1229\]
\[\dfrac{1}{ P_1} =\dfrac{1.1229 }{46.2\; mmHg}\]
\[P_1 = \dfrac{46.2\; mmHg}{1.1229}\]
\(P_1 = 41.143\; mmHg\), which gets rounded to two significant digits (from the two significant digits in 44 kJ/mol).
\(P_1\) vapor pressure is 41 mmHg.
References
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, and Jeffry D. Madura. "The Critical Point." General Chemistry: Principles & Modern Applications, ninth Edition. New Jersey: Pearson Education, Inc., 2007. 478-479.
- Freeman, P.I., Rowlinson, J.S. "Lower Critical Points in Polymer Solutions." Department of Chemistry. University of Manchester. 24 April 2003.
- Cahn, John. "Critical Wetting Point."Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts. 15 April 1977.
Outside Links
- Brown, R. J. C.; Brown, R. F. C. "Melting Point and Molecular Symmetry." J. Chem. Educ. 2000 77 724.
Contributors
- Minh Nguyen, Cynthia Dvorsky Garcia

