Closest Packed Structures
- Page ID
- 1548
The term "closest packed structures" refers to the most tightly packed or space-efficient composition of crystal structures (lattices). Imagine an atom in a crystal lattice as a sphere. While cubes may easily be stacked to fill up all empty space, unfilled space will always exist in the packing of spheres. To maximize the efficiency of packing and minimize the volume of unfilled space, the spheres must be arranged as close as possible to each other. These arrangements are called closest packed structures.
The packing of spheres can describe the solid structures of crystals. In a crystal structure, the centers of atoms, ions, or molecules lie on the lattice points. Atoms are assumed to be spherical to explain the bonding and structures of metallic crystals. These spherical particles can be packed into different arrangements. In closest packed structures, the arrangement of the spheres are densely packed in order to take up the greatest amount of space possible.
Types of Holes From Close-Packing of Spheres
When a single layer of spheres is arranged into the shape of a hexagon, gaps are left uncovered. The hole formed between three spheres is called a trigonal hole because it resembles a triangle. In the example below, two out of the the six trigonal holes have been highlighted green.
Once the first layer of spheres is laid down, a second layer may be placed on top of it. The second layer of spheres may be placed to cover the trigonal holes from the first layer. Holes now exist between the first layer (the orange spheres) and the second (the lime spheres), but this time the holes are different. The triangular-shaped hole created over a orange sphere from the first layer is known as a tetrahedral hole. A hole from the second layer that also falls directly over a hole in the first layer is called an octahedral hole.
Closest Pack Crystal Structures
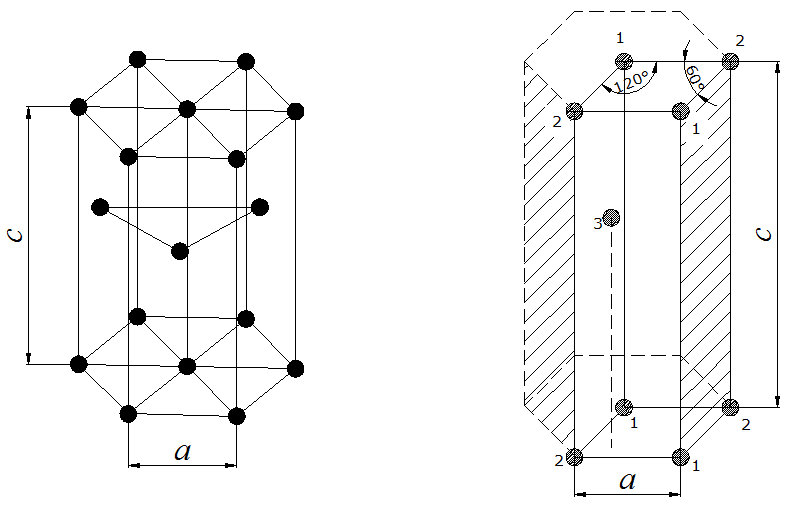
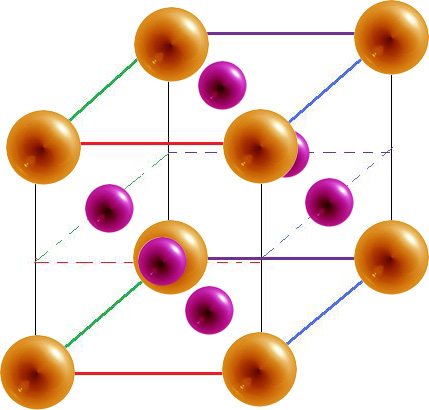
Hexagonal Closest Packed (HCP)
In a hexagonal closest packed structure, the third layer has the same arrangement of spheres as the first layer and covers all the tetrahedral holes. Since the structure repeats itself after every two layers, the stacking for hcp may be described as "a-b-a-b-a-b." The atoms in a hexagonal closest packed structure efficiently occupy 74% of space while 26% is empty space.
Cubic Closest Packed (CCP)
The arrangement in a cubic closest packing also efficiently fills up 74% of space. Similar to hexagonal closest packing, the second layer of spheres is placed on to of half of the depressions of the first layer. The third layer is completely different than that first two layers and is stacked in the depressions of the second layer, thus covering all of the octahedral holes. The spheres in the third layer are not in line with those in layer A, and the structure does not repeat until a fourth layer is added. The fourth layer is the same as the first layer, so the arrangement of layers is "a-b-c-a-b-c."
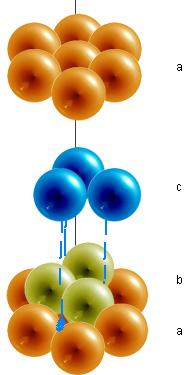
Coordination Number and Number of Atoms Per Unit Cell
A unit cell is the smallest representation of an entire crystal. All crystal lattices are built of repeating unit cells. In a unit cell, an atom's coordination number is the number of atoms it is touching.
- The hexagonal closest packed (hcp) has a coordination number of 12 and contains 6 atoms per unit cell.
- The face-centered cubic (fcc) has a coordination number of 12 and contains 4 atoms per unit cell.
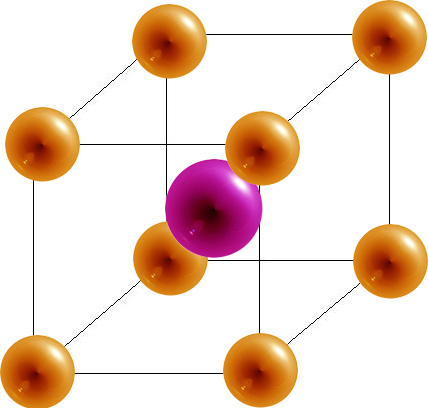
- The body-centered cubic (bcc) has a coordination number of 8 and contains 2 atoms per unit cell.
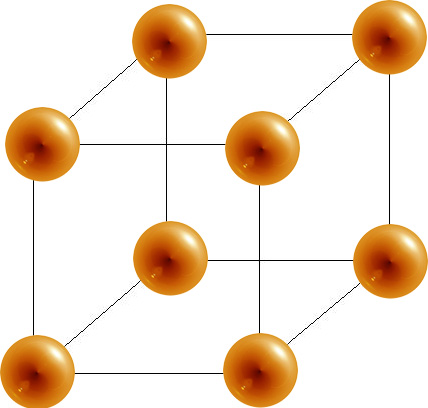
- The simple cubic has a coordination number of 6 and contains 1 atom per unit cell.
| Unit Cell | Coordination Number | # of Atoms Per Unit Cell | % space |
|---|---|---|---|
|
Simple Unit Cell
|
6 |
1 | 52% |
|
Body-Centered Cubic
|
8 | 2 | 68% |
|
Face-centered Cubic
|
12 | 4 | 74.04% |
|
Cubic Closest Packed
|
12 | 4 | 74.04% |
|
Hexagonal Closest Packed
|
12 | 6* (2) see note below | 74.04% |
*For the hexagonal close-packed structure the derivation is similar. Here the unit cell consist of three primitive unit cells is a hexagonal prism containing six atoms (if the particles in the crystal are atoms). Indeed, three are the atoms in the middle layer (inside the prism); in addition, for the top and bottom layers (on the bases of the prism), the central atom is shared with the adjacent cell, and each of the six atoms at the vertices is shared with other five adjacent cells. So the total number of atoms in the cell is 3 + (1/2)×2 + (1/6)×6×2 = 6, however this results in 2 per primitive unit cell.
References
- Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, 1993.
- Krishna, P. and Verma, A. R. Closed Packed Structures, Chester, UK: International Union of Crystallography, 1981.
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, and Jeffry D. Madura. "Crystal Structures" General Chemistry: Principles & Modern Applications, ninth Edition. New Jersey: Pearson Education, Inc., 2007. 501-508.
Contributors and Attributions
- Brittanie Harbick, Laura Suh, Jenny Fong



www.quora.com/What-is-the-nu...it-cell-of-HCP