Fission and Fusion
- Page ID
- 1480
The energy harnessed in nuclei is released in nuclear reactions. Fission is the splitting of a heavy nucleus into lighter nuclei and fusion is the combining of nuclei to form a bigger and heavier nucleus. The consequence of fission or fusion is the absorption or release of energy.
Introduction
Protons and neutrons make up a nucleus, which is the foundation of nuclear science. Fission and fusion involves the dispersal and combination of elemental nucleus and isotopes, and part of nuclear science is to understand the process behind this phenomenon. Adding up the individual masses of each of these subatomic particles of any given element will always give you a greater mass than the mass of the nucleus as a whole. The missing idea in this observation is the concept called nuclear binding energy. Nuclear binding energy is the energy required to keep the protons and neutrons of a nucleus intact, and the energy that is released during a nuclear fission or fusion is nuclear power. There are some things to consider however. The mass of an element's nucleus as a whole is less than the total mass of its individual protons and neutrons. The difference in mass can be attributed to the nuclear binding energy. Basically, nuclear binding energy is considered as mass, and that mass becomes "missing". This missing mass is called mass defect, which is the nuclear energy, also known as the mass released from the reaction as neutrons, photons, or any other trajectories. In short, mass defect and nuclear binding energy are interchangeable terms.
Nuclear Fission and Fusion
Nuclear fission is the splitting of a heavy nucleus into two lighter ones. Fission was discovered in 1938 by the German scientists Otto Hahn, Lise Meitner, and Fritz Strassmann, who bombarded a sample of uranium with neutrons in an attempt to produce new elements with Z > 92. They observed that lighter elements such as barium (Z = 56) were formed during the reaction, and they realized that such products had to originate from the neutron-induced fission of uranium-235:
\[_{92}^{235}\textrm U+\,_0^1\textrm n \rightarrow \,_{56}^{141}\textrm{Ba}+\,_{36}^{92}\textrm{Kr}+3_0^1\textrm n \label{21.6.11}\]
This hypothesis was confirmed by detecting the krypton-92 fission product. As discussed in Section 20.2, the nucleus usually divides asymmetrically rather than into two equal parts, and the fission of a given nuclide does not give the same products every time.
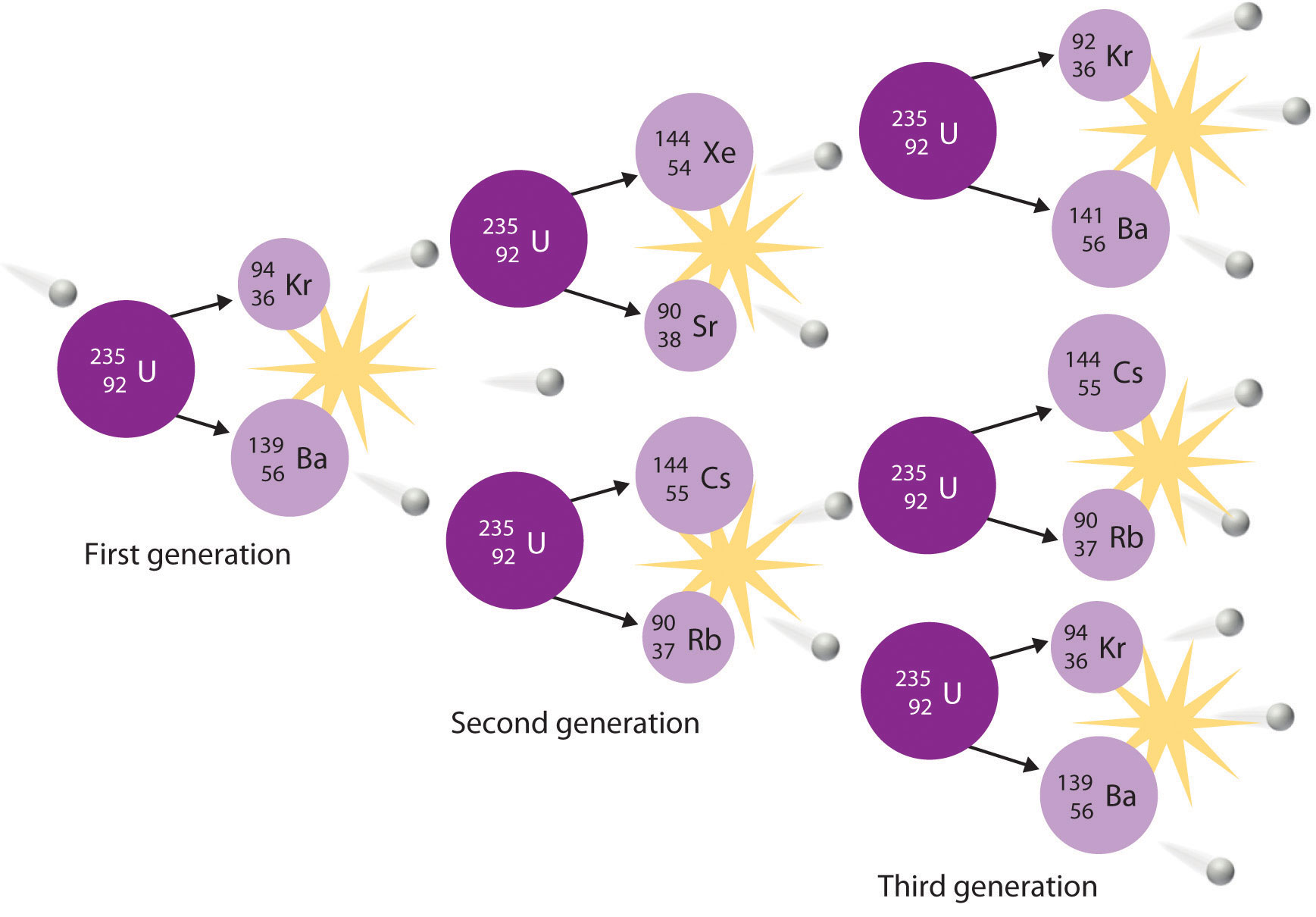
In a typical nuclear fission reaction, more than one neutron is released by each dividing nucleus. When these neutrons collide with and induce fission in other neighboring nuclei, a self-sustaining series of nuclear fission reactions known as a nuclear chain reaction can result (Figure 21.6.2). For example, the fission of 235U releases two to three neutrons per fission event. If absorbed by other 235U nuclei, those neutrons induce additional fission events, and the rate of the fission reaction increases geometrically. Each series of events is called a generation. Experimentally, it is found that some minimum mass of a fissile isotope is required to sustain a nuclear chain reaction; if the mass is too low, too many neutrons are able to escape without being captured and inducing a fission reaction. The minimum mass capable of supporting sustained fission is called the critical mass. This amount depends on the purity of the material and the shape of the mass, which corresponds to the amount of surface area available from which neutrons can escape, and on the identity of the isotope. If the mass of the fissile isotope is greater than the critical mass, then under the right conditions, the resulting supercritical mass can release energy explosively. The enormous energy released from nuclear chain reactions is responsible for the massive destruction caused by the detonation of nuclear weapons such as fission bombs, but it also forms the basis of the nuclear power industry.
Nuclear fusion, in which two light nuclei combine to produce a heavier, more stable nucleus, is the opposite of nuclear fission. As in the nuclear transmutation reactions discussed in Section 20.2, the positive charge on both nuclei results in a large electrostatic energy barrier to fusion. This barrier can be overcome if one or both particles have sufficient kinetic energy to overcome the electrostatic repulsions, allowing the two nuclei to approach close enough for a fusion reaction to occur. The principle is similar to adding heat to increase the rate of a chemical reaction. As shown in the plot of nuclear binding energy per nucleon versus atomic number in Figure 21.6.3, fusion reactions are most exothermic for the lightest element. For example, in a typical fusion reaction, two deuterium atoms combine to produce helium-3, a process known as deuterium–deuterium fusion (D–D fusion):
\[2_1^2\textrm H\rightarrow \,_2^3\textrm{He}+\,_0^1\textrm n \label{21.6.12}\]
In another reaction, a deuterium atom and a tritium atom fuse to produce helium-4 (Figure \(\PageIndex{1}\)), a process known as deuterium–tritium fusion (D–T fusion):
\[_1^2\textrm H+\,_1^3\textrm H\rightarrow \,_2^4\textrm{He}+\,_0^1\textrm n \label{21.6.13}\]
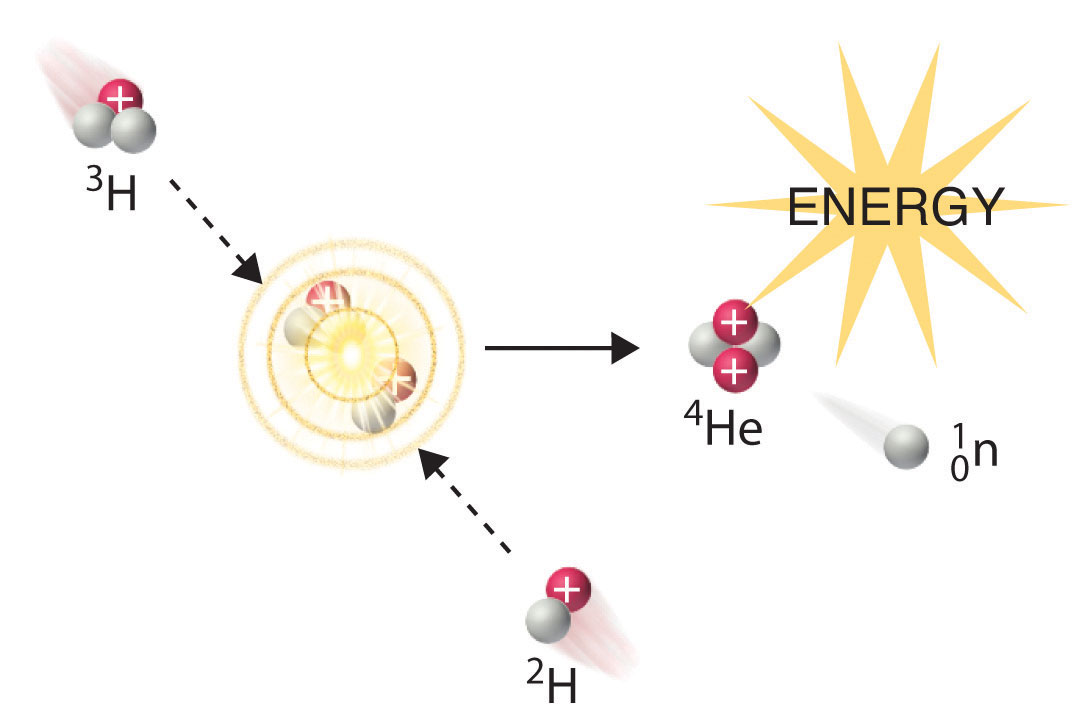
Initiating these reactions, however, requires a temperature comparable to that in the interior of the sun (approximately 1.5 × 107 K). Currently, the only method available on Earth to achieve such a temperature is the detonation of a fission bomb. For example, the so-called hydrogen bomb (or H bomb) is actually a deuterium–tritium bomb (a D–T bomb), which uses a nuclear fission reaction to create the very high temperatures needed to initiate fusion of solid lithium deuteride (6LiD), which releases neutrons that then react with 6Li, producing tritium. The deuterium-tritium reaction releases energy explosively. Example 21.6.3 and its corresponding exercise demonstrate the enormous amounts of energy produced by nuclear fission and fusion reactions. In fact, fusion reactions are the power sources for all stars, including our sun.
To calculate the energy released during mass destruction in both nuclear fission and fusion, we use Einstein’s equation that equates energy and mass:
\[ E=mc^2 \label{1} \]
with
- \(m\) is mass (kilograms),
- \(c\) is speed of light (meters/sec) and
- \(E\) is energy (Joules).
Calculate the amount of energy (in electronvolts per atom and kilojoules per mole) released when the neutron-induced fission of 235U produces 144Cs, 90Rb, and two neutrons:
\(_{92}^{235}\textrm U+\,_0^1\textrm n\rightarrow \,_{55}^{144}\textrm{Cs}+\,_{37}^{90}\textrm{Rb}+2_0^1\textrm n\)
Given: balanced nuclear reaction
Asked for: energy released in electronvolts per atom and kilojoules per mole
Strategy:
A Following the method used in Example 21.6.1, calculate the change in mass that accompanies the reaction. Convert this value to the change in energy in electronvolts per atom.
B Calculate the change in mass per mole of 235U. Then use Equation 21.6.3 to calculate the change in energy in kilojoules per mole.
Solution
A The change in mass that accompanies the reaction is as follows:
\\&=(143.932077\textrm{ amu}+89.914802\textrm{ amu}+1.008665\textrm{ amu})-\textrm{235.043930 amu}
\\&=-0.188386\textrm{ amu}\end{align}\)
The change in energy in electronvolts per atom is as follows:
B The change in mass per mole of \(_{92}^{235}\textrm{U}\) is −0.188386 g = −1.88386 × 10−4 kg, so the change in energy in kilojoules per mole is as follows:
\(\begin{align}\Delta E&=(\Delta m)c^2=(-1.88386\times10^{-4}\textrm{ kg})(2.998\times10^8\textrm{ m/s})^2
\\&=-1.693\times10^{13}\textrm{ J/mol}=-1.693\times10^{10}\textrm{ kJ/mol}\end{align}\)
Calculate the amount of energy (in electronvolts per atom and kilojoules per mole) released when deuterium and tritium fuse to give helium-4 and a neutron:
\(_1^2\textrm H+\,_1^3\textrm H\rightarrow \,_2^4\textrm{He}+\,_0^1\textrm n\)
Solution
ΔE = −17.6 MeV/atom = −1.697 × 109 kJ/mol
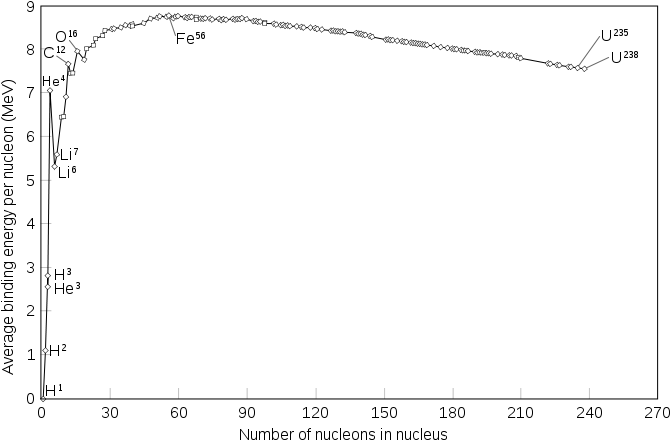
Figure \(\PageIndex{1}\): Binding energy per nucleon of common isotopes.
Fission
Fission is the splitting of a nucleus that releases free neutrons and lighter nuclei. The fission of heavy elements is highly exothermic which releases about 200 million eV compared to burning coal which only gives a few eV. The amount of energy released during nuclear fission is millions of times more efficient per mass than that of coal considering only 0.1 percent of the original nuclei is converted to energy. Daughter nucleus, energy, and particles such as neutrons are released as a result of the reaction. The particles released can then react with other radioactive materials which in turn will release daughter nucleus and more particles as a result, and so on. The unique feature of nuclear fission reactions is that they can be harnessed and used in chain reactions. This chain reaction is the basis of nuclear weapons. One of the well known elements used in nuclear fission is \(\ce{^{235}U}\), which when is bombarded with a neutron, the atom turns into \(\ce{^{236}U}\) which is even more unstable and splits into daughter nuclei such as Krypton-92 and Barium-141 and free neutrons. The resulting fission products are highly radioactive, commonly undergoing \(\beta^-\) decay.
Nuclear fission is the splitting of the nucleus of an atom into nuclei of lighter atoms, accompanied by the release of energy, brought on by a neutron bombardment. The original concept of this nuclei splitting was discovered by Enrico Femi in 1934—who believed transuranium elements might be produced by bombarding uranium with neutrons, because the loss of Beta particles would increase the atomic number. However, the products that formed did not correlate with the properties of elements with higher atomic numbers than uranium (Ra, Ac, Th, and Pa). Instead, they were radioisotopes of much lighter elements such as Sr and Ba. The amount of mass lost in the fission process is equivalent to an energy of \(3.20 \times 10^{-11}\; J\).
Consider the neutron bonbardment
\[ \ce{_{92}^{235}U + _{1}^{0}n \rightarrow _{92}^{236}U} \rightarrow \; \text{fission products} \]
which releases \(3.20 \times 10^{-11}\; J\) per \(\ce{^{235}U}\) atom.
How much energy would be released if \(1.00\;g\) of \(\ce{^{235}U}\) were to undergo fission?
Solution
\[ (1.00\;\rm{g}\; \ce{^{235}U} ) \times \left(\dfrac{1\; mol\; \ce{^{235}U}}{235\; g\; \ce{^{235}U}}\right) \times \left(\dfrac{ 6.022 \times 10^{23}\; \text{atoms}\; \ce{^{235}U}}{1\; mol\; \ce{^{235}U}} \right) \times \left(\dfrac{3.20 \times 10^{-11}\; J}{1\; atom \; \ce{^{235}U}}\right) = 8.20 \times 10^{10}\; J\]
Clearly, the fission of a small amount of atoms can produce an enormous amount of energy, in the form of warmth and radiation (gamma waves). When an atom splits, each of the two new particles contains roughly half the neutrons and protons of the original nucleus, and in some cases a 2:3 ratio.
Critical Mass
The explosion of a bomb only occurs if the chain reaction exceeds its critical mass. The critical mass is the point at which a chain reaction becomes self-sustaining. If the neutrons are lost at a faster rate than they are formed by fission, the reaction will not be self-sustaining. The spontaneous nuclear fission rate is the probability per second that a given atom will fission spontaneously--that is, without any external intervention. In nuclear power plants, nuclear fission is controlled by a medium such as water in the nuclear reactor. The water acts as a heat transfer medium to cool down the reactor and to slow down neutron particles. This way, the neutron emission and usage is a controlled. If nuclear reaction is not controlled because of lack of cooling water for example, then a meltdown will occur.
Fusion
Nuclear fusion is the joining of two nuclei to form a heavier nuclei. The reaction is followed either by a release or absorption of energy. Fusion of nuclei with lower mass than iron releases energy while fusion of nuclei heavier than iron generally absorbs energy. This phenomenon is known as iron peak. The opposite occurs with nuclear fission.
The power of the energy in a fusion reaction is what drives the energy that is released from the sun and a lot of stars in the universe. Nuclear fusion is also applied in nuclear weapons, specifically, a hydrogen bomb. Nuclear fusion is the energy supplying process that occurs at extremely high temperatures like in stars such as the sun, where smaller nuclei are joined to make a larger nucleus, a process that gives off great amounts of heat and radiation. When uncontrolled, this process can provide almost unlimited sources of energy and an uncontrolled chain provides the basis for a hydrogen bond, since most commonly hydrogen is fused. Also, the combination of deuterium atoms to form helium atoms fuel this thermonuclear process. For example:
\[ \ce{^2_1H + ^3_1H \rightarrow ^4_2He + ^1_0n} + \text{energy}\]
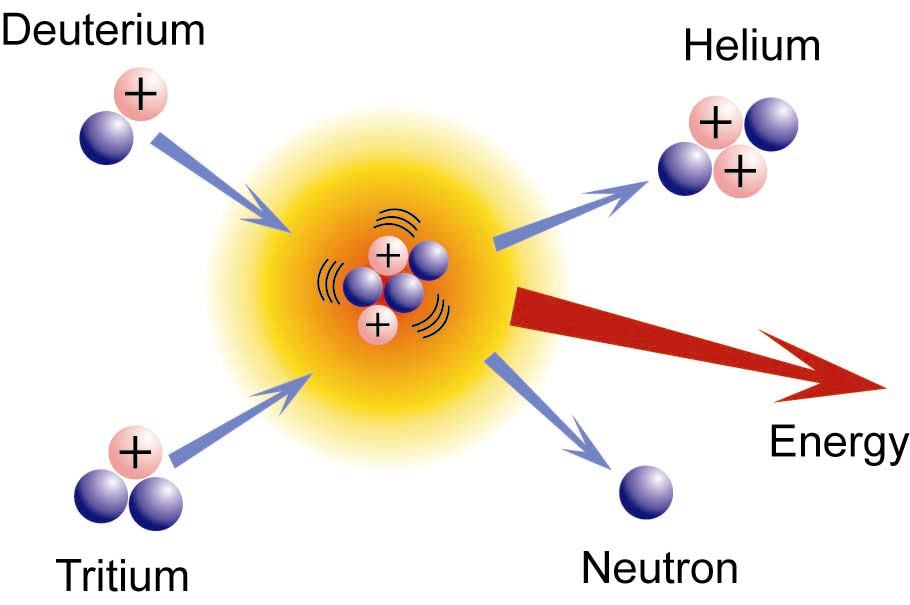
However, a controlled fusion reaction has yet to be fully demonstrated due to many problems that present themselves including the difficulty of forcing deuterium and tritium nuclei within a close proximity, achieving high enough thermal energies, and completely ionizing gases into plasma. A necessary part in nuclear fusion is plasma, which is a mixture of atomic nuclei and electrons that are required to initiate a self-sustaining reaction which requires a temperature of more than 40,000,000 K. Why does it take so much heat to achieve nuclear fusion even for light elements such as hydrogen? The reason is because the nucleus contain protons, and in order to overcome electrostatic repulsion by the protons of both the hydrogen atoms, both of the hydrogen nucleus needs to accelerate at a super high speed and get close enough in order for the nuclear force to start fusion. The result of nuclear fusion releases more energy than it takes to start the fusion so ΔG of the system is negative which means that the reaction is exothermic. And because it is exothermic, the fusion of light elements is self-sustaining given that there is enough energy to start fusion in the first place.

Figure \(\PageIndex{1}\): Scientists have yet to find a method for controlling fusion reactions. Fission reactions on the other hand is the type used in nuclear power plants and can be controlled. Atomic bombs and hydrogen bombs are examples of uncontrolled nuclear reactions.
References
- Petrucci, Harwood, Herring, Madura. General Chemistry: Principles & Modern Applications (9th edition). New Jersey: Pearson Education, 2007.
- William E. Stephens. Nuclear Fission and Atomic Energy. Inman Press 2007.
- Petrucci, Herring, Madura, Bissonnette. General Chemistry: Principles & Modern Applications (10th edition). New Jersey: Pearson Education, 2011.
- "Nuclear Fission vs Nuclear Fusion - Difference and Comparison | Diffen." Diffen - Compare Anything. Diffen. Discern. Decide. Web. 04 June 2011. <http://www.diffen.com/difference/Nuc...Nuclear_Fusion>.

