2. Strong and Weak Acids
- Page ID
- 3852
This page explains the terms strong and weak as applied to acids. As a part of this it defines and explains what is meant by pH, Ka and pKa.
Strong acids
We are going to use the Bronsted-Lowry definition of an acid. When an acid dissolves in water, a proton (hydrogen ion) is transferred to a water molecule to produce a hydroxonium ion and a negative ion depending on what acid you are starting from.
In the general case . . .
\[HA + H_2O \rightleftharpoons H_3O^+ + A^- \tag{1}\]
These reactions are all reversible, but in some cases, the acid is so good at giving away hydrogen ions that we can think of the reaction as being one-way. The acid is virtually 100% ionized.
For example, when hydrogen chloride dissolves in water to make hydrochloric acid, so little of the reverse reaction happens that we can write:
\[ H_2O_{(l)} + HCl_{(g)} \rightarrow H_3O^+_{(aq)} + Cl^-_{(aq)} \tag{2}\]
At any one time, virtually 100% of the hydrogen chloride will have reacted to produce hydroxonium ions and chloride ions. Hydrogen chloride is described as a strong acid.
A strong acid is one which is virtually 100% ionized in solution.
Other common strong acids include sulphuric acid and nitric acid.
You may find the equation for the ionization written in a simplified form:
\[ HCl_{(aq)} \rightarrow H^+_{(aq)} + Cl^-_{(aq)} \tag{3}\]
This shows the hydrogen chloride dissolved in the water splitting to give hydrogen ions in solution and chloride ions in solution.
This version is often used in this work just to make things look easier. If you use it, remember that the water is actually involved, and that when you write H+(aq) what you really mean is a hydroxonium ion, H3O+.
Strong acids and pH
pH is a measure of the concentration of hydrogen ions in a solution. Strong acids like hydrochloric acid at the sort of concentrations you normally use in the lab have a pH around 0 to 1. The lower the pH, the higher the concentration of hydrogen ions in the solution.
Defining pH
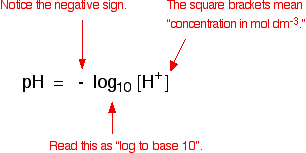
Suppose you had to work out the pH of 0.1 mol dm-3 hydrochloric acid. All you have to do is work out the concentration of the hydrogen ions in the solution, and then use your calculator to convert it to a pH.
With strong acids this is easy.
Hydrochloric acid is a strong acid - virtually 100% ionized. Each mole of HCl reacts with the water to give 1 mole of hydrogen ions and 1 mole of chloride ions
That means that if the concentration of the acid is 0.1 mol dm-3, then the concentration of hydrogen ions is also 0.1 mol dm-3.
Use your calculator to convert this into pH. My calculator wants me to enter 0.1, and then press the "log" button. Yours might want you to do it in a different order. You need to find out!
log10 [0.1] = -1
But pH = - log10 [0.1]
- (-1) = 1
The pH of this acid is 1.
Weak acids
A weak acid is one which doesn't ionize fully when it is dissolved in water. Ethanoic acid is a typical weak acid. It reacts with water to produce hydroxonium ions and ethanoate ions, but the back reaction is more successful than the forward one. The ions react very easily to reform the acid and the water.
\[ CH_3COOH + H_2O \rightleftharpoons CH_3COO^- + H_3O^+ \tag{4}\]
At any one time, only about 1% of the ethanoic acid molecules have converted into ions. The rest remain as simple ethanoic acid molecules. Most organic acids are weak. Hydrogen fluoride (dissolving in water to produce hydrofluoric acid) is a weak inorganic acid that you may come across elsewhere.
Comparing the strengths of weak acids
The position of equilibrium of the reaction between the acid and water varies from one weak acid to another. The further to the left it lies, the weaker the acid is.
\[HA + H_2O \rightleftharpoons H_3O^+ + A^- \tag{5}\]
The acid dissociation constant, Ka
You can get a measure of the position of an equilibrium by writing an equilibrium constant for the reaction. The lower the value for the constant, the more the equilibrium lies to the left. The dissociation (ionization) of an acid is an example of a homogeneous reaction. Everything is present in the same phase - in this case, in solution in water. You can therefore write a simple expression for the equilibrium constant, Kc. Here is the equilibrium again:
\[HA + H_2O \rightleftharpoons H_3O^+ + A^- \tag{5}\]
You might expect the equilibrium constant to be written as:
\[]K_c = \dfrac{[H_3O^+][A^-]}{[HA][H_2O]} \]
However, if you think about this carefully, there is something odd about it.
At the bottom of the expression, you have a term for the concentration of the water in the solution. That's not a problem - except that the number is going to be very large compared with all the other numbers.
In 1 dm3 of solution, there are going to be about 55 moles of water.
If you had a weak acid with a concentration of about 1 mol dm-3, and only about 1% of it reacted with the water, the number of moles of water is only going to fall by about 0.01. In other words, if the acid is weak the concentration of the water is virtually constant. In that case, there isn't a lot of point in including it in the expression as if it were a variable. Instead, a new equilibrium constant is defined which leaves it out. This new equilibrium constant is called Ka.
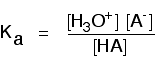
You may find the Ka expression written differently if you work from the simplified version of the equilibrium reaction:
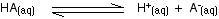
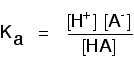
This may be written with or without state symbols.
It is actually exactly the same as the previous expression for Ka! Remember that although we often write H+ for hydrogen ions in solution, what we are actually talking about are hydroxonium ions. This second version of the Ka expression is not as precise as the first one.
To take a specific common example, the equilibrium for the dissociation of ethanoic acid is properly written as:
\[CH_3COOH + H_2O \rightleftharpoons CH_3COO^- + H_3O^+ \tag{7}\]
The Ka expression is:
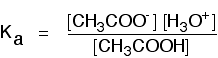
If you are using the simpler version of the equilibrium . . .
\[CH_3COOH \rightleftharpoons CH_3COO^- + H^+ \tag{8}\]
. . . the Ka expression is:

The table shows some values of Ka for some simple acids:
| acid | Ka (mol dm-3) |
|---|---|
| hydrofluoric acid | 5.6 x 10-4 |
| methanoic acid | 1.6 x 10-4 |
| ethanoic acid | 1.7 x 10-5 |
| hydrogen sulphide | 8.9 x 10-8 |
These are all weak acids because the values for Ka are very small. They are listed in order of decreasing acid strength - the Ka values get smaller as you go down the table. However, if you aren't very happy with numbers, that isn't immediately obvious. Because the numbers are in two parts, there is too much to think about quickly! To avoid this, the numbers are often converted into a new, easier form, called pKa.
An introduction to pKa
pKa bears exactly the same relationship to Ka as pH does to the hydrogen ion concentration:
\[pK_a = -\log_{10} K_a \tag{9}\]
If you use your calculator on all the Ka values in the table above and convert them into pKa values, you get:
| acid | Ka (mol dm-3) | pKa |
|---|---|---|
| hydrofluoric acid | 5.6 x 10-4 | 3.3 |
| methanoic acid | 1.6 x 10-4 | 3.8 |
| ethanoic acid | 1.7 x 10-5 | 4.8 |
| hydrogen sulphide | 8.9 x 10-8 | 7.1 |
Notice that the weaker the acid, the larger the value of pKa. It is now easy to see the trend towards weaker acids as you go down the table.
- The lower the value for pKa, the stronger the acid.
- The higher the value for pKa, the weaker the acid.


