12.4: Ensemble Averaging and Line-Broadening

We have seen that an absorption lineshape can represent the dynamics of the dipole or be broadened by energy relaxation, for instance through coupling to a continuum. However, there are numerous processes that can influence the lineshape. These can be separated by dynamic processes intrinsic to the molecular system, which is termed homogeneous broadening, and static effects known as inhomogeneous broadening, which can be considered an ensemble averaging effect. To illustrate, imagine that the dipole correlation function has an oscillatory, damped form

\[C _ {\mu \mu} (t) = \sum _ {g , e} p _ {g} \left| \mu _ {e g} \right|^{2} \exp \left[ - i \omega _ {e g} t - \Gamma t \right] \label{11.59}\]

Then the Fourier transform would give a lineshape

\[\operatorname {Re} \left[ \tilde {C} _ {\mu \mu} ( \omega ) \right] = \sum _ {g , e} p _ {g} \frac {\left| \mu _ {e g} \right|^{2} \Gamma} {\left( \omega - \omega _ {e g} \right)^{2} - \Gamma^{2}} \label{11.60}\]

Here the homogeneous effects are reflected in the factor \(\Gamma\), the damping rate and linewidth, whereas inhomogeneous effects arise from averaging over the ensemble.

Homogeneous Broadening

Several dynamical mechanisms can potentially contribute to damping and line-broadening. These intrinsically molecular processes, often referred to as homogeneous broadening, are commonly assigned a time scale \(T _ {2} = \Gamma^{- 1}\).

Population Relaxation

Population relaxation refers to decay in the coherence created by the light field as a result of the finite lifetime of the coupled states, and is often assigned a time scale \(T_1\). This can have contributions from radiative decay, such as spontaneous emission, or non-radiative processes such as relaxation as a result of coupling to a continuum.

\[\frac {1} {T _ {1}} = \frac {1} {\tau _ {r a d}} + \frac {1} {\tau _ {N R}} \label{11.61}\]

The observed population relaxation time depends on both the relaxation times of the upper and lower states (\(m\) and \(n\)) being coupled by the field:

\[1 / T _ {1} = w _ {m n} + w _ {n m}.\]

When the energy splitting is high compared to \(k_BT\), only the downward rate contributes, which is why the rate is often written \(1/2T_1\).

Pure Dephasing

Pure dephasing is characterized by a time constant \(T_2^{*}\) that characterizes the randomization of phase within an ensemble as a result of molecular interactions. This is a dynamic effect in which memory of the phase of oscillation of a molecule is lost as a result of intermolecular interactions that randomize the phase. Examples include collisions in a dense gas, or fluctuations induced by a solvent. This process does not change the population of the states involved.

Orientational Relaxation

Orientational relaxation (\(\tau_{or}\)) also leads to relaxation of the dipole correlation function and to line-broadening. Since the correlation function depends on the projection of the dipole onto a fixed axis in the laboratory frame, randomization of the initial dipole orientations is an ensemble averaged dephasing effect. In solution, this process is commonly treated as an orientational diffusion problem in which \(\tau_{or}\) is proportional to the diffusion constant.

If these homogeneous processes are independent, the rates for different processes contribute additively to the damping and line width:

\[\frac {1} {T _ {2}} = \frac {1} {T _ {1}} + \frac {1} {T _ {2}^{*}} + \frac {1} {\tau _ {o r}} \label{11.62}\]

Inhomogeneous Broadening

Absorption lineshapes can also be broadened by a static distribution of frequencies. If molecules within the ensemble are influenced static environmental variations more than other processes, then the observed lineshape reports on the distribution of environments. This inhomogeneous broadening is a static ensemble averaging effect, which hides the dynamical content in the homogeneous linewidth. The origin of the inhomogeneous broadening can be molecular (for instance a distribution of defects in crystals) or macroscopic (i.e., an inhomogeneous magnetic field in NMR).

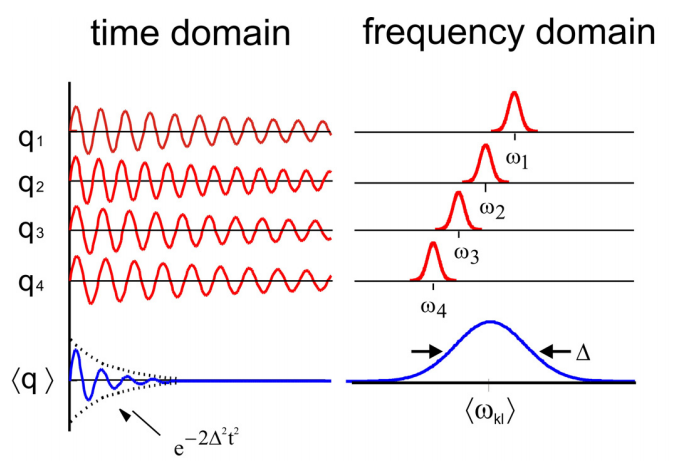
The inhomogeneous linewidth is dictated the width of the distribution \(\Delta\).

Total Linewidth

The total observed broadening of the absorption lineshape reflects the contribution of all of these effects:

\[C _ {\mu \mu} \propto \exp \left[ - i \omega _ {e g} t - \left( \frac {1} {T _ {2}^{*}} + \frac {1} {2 T _ {1}} + \frac {1} {\tau _ {o r}} \right) t - \frac {\Delta^{2}} {2} t^{2} \right] \label{11.63}\]

These effects can be wrapped into a lineshape function \(g(t)\). The lineshape for the broadening of a given transition can be written as the Fourier transform over the oscillating transition frequency damped and modulated by a complex \(g(t)\):

\[\sigma ( \omega ) = \int _ {- \infty}^{+ \infty} d t \, e^{i \omega t} e^{- i \omega _ {eg} t - g (t)} \label{11.64}\]

All of these effects can be present simultaneously in an absorption spectrum.