3.7: Time-Dependent Perturbation Theory
- Page ID
- 107397
Perturbation theory refers to calculating the time-dependence of a system by truncating the expansion of the interaction picture time-evolution operator after a certain term. In practice, truncating the full time-propagator \(U\) is not effective, and only works well for times short compared to the inverse of the energy splitting between coupled states of your Hamiltonian. The interaction picture applies to Hamiltonians that can be cast as
\[H=H_o + V(t)\]
and allows us to focus on the influence of the coupling. We can then treat the time evolution under \(H_o\) exactly, but truncate the influence of \(V(t)\). This works well for weak perturbations. Let’s look more closely at this.
We know the eigenstates for \(H_o\):
\[H _ {0} | n \rangle = E _ {n} | n \rangle\]
and we can calculate the evolution of the wavefunction that results from \(V(t)\):
\[| \psi _ {I} (t) \rangle = \sum _ {n} b _ {n} (t) | n \rangle \label{2.117}\]
For a given state \(k\), we calculate \(b_k(t)\) as:
\[b _ {k} = \left\langle k \left| U _ {I} \left( t , t _ {0} \right) \right| \psi \left( t _ {0} \right) \right\rangle \label{2.118}\]
where
\[U _ {I} \left( t , t _ {0} \right) = \exp _ {+} \left[ \frac {- i} {\hbar} \int _ {t _ {0}}^{t} V _ {I} ( \tau ) d \tau \right ]\label{2.119}\]
Now we can truncate the expansion after a few terms. This works well for small changes in amplitude of the quantum states with small coupling matrix elements relative to the energy splittings involved (\(\left| b _ {k} (t) \right| \approx \left| b _ {k} ( 0 ) \right| ; | V | \ll \left| E _ {k} - E _ {n} \right|\)). As we will see, the results we obtain from perturbation theory are widely used for spectroscopy, condensed phase dynamics, and relaxation. Let’s take the specific case where we have a system prepared in , and we want to know the probability of observing the system in \(| k \rangle\) at time \(t\) due to \(V(t)\):
\[P _ {k} (t) = \left| b _ {k} (t) \right|^{2}] \label{2.120}.\]
Expanding
\[b _ {k} (t) = \langle k | \exp _ {+} \left[ - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau V _ {I} ( \tau ) \right] \ell \rangle\]
\[\left.\begin{aligned} b _ {k} (t) = \langle k | \ell \rangle & - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau \left\langle k \left| V _ {I} ( \tau ) \right| \ell \right\rangle \\ & + \left( \frac {- i} {\hbar} \right)^{2} \int _ {t _ {0}}^{t} d \tau _ {2} \int _ {t _ {0}}^{\tau _ {2}} d \tau _ {1} \left\langle k \left| V _ {I} \left( \tau _ {2} \right) V _ {I} \left( \tau _ {1} \right) \right| \ell \right\rangle + \ldots \end{aligned} \right. \label{2.121}\]
Now, using
\[\left\langle k \left| V _ {I} (t) \right| \ell \right\rangle = \left\langle k \left| U _ {0}^{\dagger} V (t) U _ {0} \right| \ell \right\rangle = e^{- i \omega _ {l k} t} V _ {k \ell} (t) \label{2.122}\]
we obtain:
\[b _ {k} (t) = \delta _ {k \ell} - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau _ {1} e^{- i \omega _ {l k} \tau _ {1}} V _ {k \ell} \left( \tau _ {1} \right) "first-order” \label{2.123}\]
\[+ \sum _ {m} \left( \frac {- i} {\hbar} \right)^{2} \int _ {t _ {0}}^{t} d \tau _ {2} \int _ {t _ {0}}^{\tau _ {2}} d \tau _ {1} e^{- i \omega _ {m k} \tau _ {2}} V _ {k n} \left( \tau _ {2} \right) e^{- i \omega _ {\ln t _ {1}}} V _ {m \ell} \left( \tau _ {1} \right) \label{2.124}\]
\[ + ...\]
The first-order term allows only direct transitions between \(| \ell \rangle\) and \(| k \rangle\), as allowed by the matrix element in \(V\), whereas the second-order term accounts for transitions occurring through all possible intermediate states \(| m \rangle\). For perturbation theory, the time-ordered integral is truncated at the appropriate order. Including only the first integral is first-order perturbation theory. The order of perturbation theory that one would extend a calculation should be evaluated initially by which allowed pathways between \(| \ell \rangle\) and \(| k \rangle\) you need to account for and which ones are allowed by the matrix elements.
For first-order perturbation theory, the expression in Equation \ref{2.123} is the solution to the differential equation that you get for direct coupling between \(| \ell \rangle\) and \(| k \rangle\):
\[\frac {\partial} {\partial t} b _ {k} = \frac {- i} {\hbar} e^{- i \omega _ {a x} t} V _ {k \ell} (t) b _ {\ell} ( 0 ) \label{2.125}\]
This indicates that the solution does not allow for the feedback between \(| \ell \rangle\) and \(| k \rangle\) that accounts for changing populations. This is the reason we say that validity dictates
\[\left| b _ {k} (t) \right|^{2} - \left| b _ {k} ( 0 ) \right|^{2} \ll 1.\]
If the initial state of the system \(\left|\psi_{0}\right\rangle\) is not an eigenstate of \(H_0\), we can express it as a superposition of eigenstates,
\[b _ {k} (t) = \sum _ {n} b _ {n} ( 0 ) \left\langle k \left| U _ {I} \right| n \right\rangle \label{2.126}\]
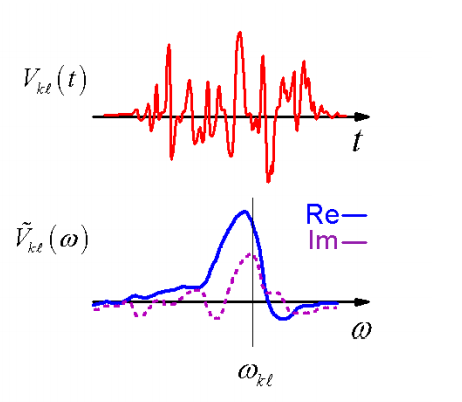
Another observation applies to first-order perturbation theory. If the system is initially prepared in a state \(| \ell \rangle\), and a time-dependent perturbation is turned on and then turned off over the time interval \(t=-\infty \text {to}+\infty\), then the complex amplitude in the target state \(| k \rangle\) is just related to the Fourier transform of \(V_{\ell k}(t)\) evaluated at the energy gap \(\omega_{\ell k}\).
\[b _ {k} (t) = - \frac {i} {\hbar} \int _ {- \infty}^{+ \infty} d \tau \,e^{- i \omega _ {\ell k} \tau} V _ {k \ell} ( \tau ) \label{2.127}\]
If the Fourier transform pair is defined in the following manner:
\[\tilde {V} ( \omega ) \equiv \tilde {\mathcal {F}} [ V (t) ] = \int _ {- \infty}^{+ \infty} d t \,V (t) \exp ( i \omega t ) \label{2.128}\]
\[V (t) \equiv \tilde {\mathcal {F}}^{- 1} [ \tilde {V} ( \omega ) ] = \frac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d \omega\, \tilde {V} ( \omega ) \exp ( - i \omega t ) \label{2.129}\]
Then we can write the probability of transfer to state \(k\) as
\[P _ {k \ell} = \frac {2 \pi \left| \tilde {V} _ {k \ell} \left( \omega _ {k \ell} \right) \right|^{2}} {\hbar^{2}} \label{2.130}\]
Example: First-order Perturbation Theory
Let’s consider a simple model for vibrational excitation induced by the compression of harmonic oscillator. We will subject a harmonic oscillator initially in its ground state to a Gaussian compression pulse, which increases its force constant.
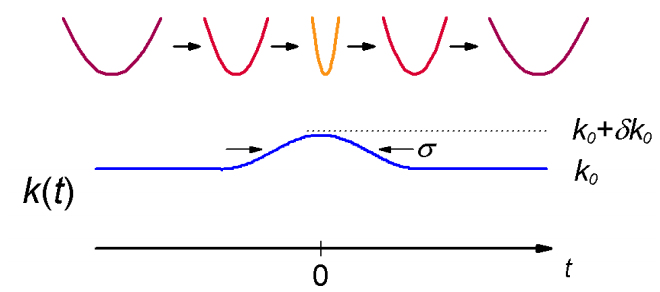
First, write the complete time-dependent Hamiltonian:
\[H (t) = T + V (t) = \frac {p^{2}} {2 m} + \frac {1} {2} k (t) x^{2} \label{2.131}\]
Now, partition it according to \(H=H_o + V(t) \) in such a manner that we can write \(H_o\) as a harmonic oscillator Hamiltonian. This involves partitioning the time-dependent force constant into two parts:
\[k (t) = k _ {0} + \delta k (t)\]
\[k _ {0} = m \Omega^{2}\]
\[\delta k (t) = \delta k _ {0} \exp \left( - \frac {\left( t - t _ {0} \right)^{2}} {2 \sigma^{2}} \right) \label{2.133}\]
\[H=\underbrace{\frac{p^{2}}{2 m}+\frac{1}{2} k_{0} x^{2}}_{H_{0}}+\underbrace{\frac{1}{2} \delta k_{0} x^{2} \exp \left(-\frac{\left(t-t_{0}\right)^{2}}{2 \sigma^{2}}\right)}_{V(t)}\]
Here \(\delta k _ {0}\) is the magnitude of the induced change in the force constant, and \(\sigma\) is the time-width of the Gaussian perturbation. So, we know the eigenstates of \(H_0\): \(H _ {0} | n \rangle = E _ {n} | n \rangle\)
\[H_{0}=\hbar \Omega\left(a^{\dagger} a+\frac{1}{2}\right)\]
and
\[E _ {n} = \hbar \Omega \left( n + \frac {1} {2} \right)\]
Now we ask, if the system is in \(|0\rangle\) before applying the perturbation, what is the probability of finding it in state n after the perturbation?
For \(n \neq 0\)
\[b _ {n} (t) = \frac {- i} {\hbar} \int _ {t _ {0}}^{t} d \tau V _ {n 0} ( \tau ) e^{i \omega _ {n 0} \tau} \label{2.135}\]
Using
\[\omega _ {n 0} = \left( E _ {n} - E _ {0} \right) / \hbar = n \Omega\]
and recognizing that we can set the limits to \(t_{0}=-\infty \text {and} \mathrm{t}=\infty\)
\[b _ {n} (t) = \frac {- i} {2 \hbar} \delta k _ {0} \left\langle n \left| x^{2} \right| 0 \right\rangle \int _ {- \infty}^{+ \infty} d \tau e^{i n \Omega \tau} e^{- \tau^{2} / 2 \sigma^{2}} \label{2.136}\]
This leads to
\[b _ {n} (t) = \frac {- i} {2 \hbar} \delta k _ {0} \sqrt {2 \pi} \sigma \left\langle n \left| x^{2} \right| 0 \right\rangle e^{- n^{2} \sigma^{2} \Omega^{2} / 2} \label{2.137}\]
Here we made use of an important identity for Gaussian integrals:
\[\int _ {- \infty}^{+ \infty} \exp \left( a x^{2} + b x + c \right) d x = \sqrt {\frac {- \pi} {a}} \exp \left( c - \frac {1} {4} \frac {b^{2}} {a} \right) \label{2.138}\]
and
\[\int _ {- \infty}^{+ \infty} \exp \left( - a x^{2} + i b x \right) d x = \sqrt {\frac {\pi} {a}} \exp \left( - \frac {b^{2}} {4 a} \right) \label{2.139}\]
What about the matrix element?
\[x^{2} = \frac {\hbar} {2 m \Omega} \left( a + a^{\dagger} \right)^{2} = \frac {\hbar} {2 m \Omega} \left( a a + a^{\dagger} a + a a^{\dagger} + a^{\dagger} a^{\dagger} \right)\label{2.140}\]
From these we see that first-order perturbation theory will not allow transitions to \(n =1\), only \(n = 0\) and \(n = 2\). Generally this would not be realistic, because you would certainly expect excitation to \(n=1\) would dominate over excitation to \(n=2\). A real system would also be anharmonic, in which case, the leading term in the expansion of the potential V(x), that is linear in x, would not vanish as it does for a harmonic oscillator, and this would lead to matrix elements that raise and lower the excitation by one quantum.
However for the present case,
\[\left\langle 2 \left| x^{2} \right| 0 \right\rangle = \sqrt {2} \frac {\hbar} {2 m \Omega} \label{2.141}\]
So,
\[b _ {2} = \frac {- i \sqrt {\pi} \delta k _ {0} \sigma} {2 m \Omega} e^{- 2 \sigma^{2} \Omega^{2}} \label{2.142}\]
and we can write the probability of occupying the \(n = 2\) state as
\[P _ {2} = \left| b _ {2} \right|^{2} = \frac {\pi \delta k _ {0}^{2} \sigma^{2}} {2 m^{2} \Omega^{2}} e^{- 4 \sigma^{2} \Omega^{2}} \label{2.143}\]
From the exponential argument, significant transfer of amplitude occurs when the compression pulse width is small compared to the vibrational period.
\[\sigma \ll \dfrac {1} {\Omega} \label{2.144}\]
In this regime, the potential is changing faster than the atoms can respond to the perturbation. In practice, when considering a solid-state problem, with frequencies matching those of acoustic phonons and unit cell dimensions, we need perturbations that move faster than the speed of sound, i.e., a shock wave. The opposite limit, \(\sigma \Omega > > 1\), is the adiabatic limit. In this case, the perturbation is so slow that the system always remains entirely in n=0, even while it is compressed.
Now, let’s consider the validity of this first-order treatment. Perturbation theory does not allow for \(b_n\) to change much from its initial value. First we re-write Equation \ref{2.143} as
\[P _ {2} = \sigma^{2} \Omega^{2} \frac {\pi} {2} \left( \frac {\delta k _ {0}^{2}} {k _ {0}^{2}} \right) e^{- 4 \sigma^{2} \Omega^{2}} \label{2.145}\]
Now for changes that don’t differ much from the initial value, \(P _ {2} \ll 1\)
\[\sigma^{2} \Omega^{2} \frac {\pi} {2} \left( \frac {\delta k _ {0}^{2}} {k _ {0}^{2}} \right) \ll 1 \label{2.146}\]
Generally, the magnitude of the perturbation \(\delta k _ {0}\) must be small compared to \(k_0\).
One step further…
The preceding example was simple, but it tracks the general approach to setting up problems that you treat with time-dependent perturbation theory. The approach relies on writing a Hamiltonian that can be cast into a Hamiltonian that you can treat exactly \(H_0\), and time-dependent perturbations that shift amplitudes between its eigenstates. For this scheme to work well, we need the magnitude of perturbation to be small, which immediately suggests working with a Taylor series expansion of the potential. For instance, take a one-dimensional potential for a bound particle, \(V(x)\), which is dependent on the form of an external variable y. We can expand the potential in x about its minimum \(x = 0\) as
\[\begin{align} V (x) &= \frac {1} {2 !} \left. \frac {\partial^{2} V} {\partial x^{2}} \right| _ {x = 0} x^{2} + \frac {1} {2 !} \left. \frac {\partial^{2} V} {\partial x \partial y} \right| _ {x = 0} x y + \frac {1} {3 !} \sum _ {y , z} \left. \frac {\partial^{3} V} {\partial x \partial y \partial z} \right| _ {x = 0} x y z + \cdots \label{2.147} \\ &= \frac {1} {2} k x^{2} + V^{( 2 )} x y + \left( V _ {3}^{( 3 )} x^{3} + V _ {2}^{( 3 )} x^{2} y + V _ {1}^{( 3 )} x y^{2} \right) + \cdots\end{align}\]
The first term is the harmonic force constant for \(x\), and the second term is a bi-linear coupling whose magnitude \(V^{(2)}\) indicates how much a change in the variable y influences the variable \(x\). The remaining terms are cubic expansion terms. \(V_3^{(3)}\) is the cubic anharmonicity of \(V(x)\), and the remaining two terms are cubic couplings that describe the dependence of x and y. Introducing a time-dependent potential is equivalent to introducing a time-dependence to the operator y, where the form and strength of the interaction is subsumed into the amplitude \(V\). In the case of the previous example, our formulation of the problem was equivalent to selecting only the \(V _ {2}^{( 3 )}\) term, so that \(\delta k _ {0} / 2 = V _ {2}^{( 3 )}\), and giving the value of y a time-dependence described by the Gaussian waveform.
Readings
- Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Quantum Mechanics. Wiley-Interscience: Paris, 1977; p. 1285.
- Nitzan, A., Chemical Dynamics in Condensed Phases. Oxford University Press: New York, 2006; Ch. 4.
- Sakurai, J. J., Modern Quantum Mechanics, Revised Edition. Addison-Wesley: Reading, MA, 1994; Ch. 2.


