3.3: Transitions Induced by Time-Dependent Potential

For many time-dependent problems, most notably in spectroscopy, we can often partition the problem so that the time-dependent Hamiltonian contains a time-independent part \(H_0\) that we can describe exactly, and a time-dependent potential \(V(t)\)

\[H = H _ {0} + V (t) \label{2.45}\]

The remaining degrees of freedom are discarded, and then only enter in the sense that they give rise to the interaction potential with \(H_0\). This is effective if you have reason to believe that the external Hamiltonian can be treated classically, or if the influence of \(H_0\) on the other degrees of freedom is negligible. From Equation \ref{2.45}, there is a straightforward approach to describing the time evolving wavefunction for the system in terms of the eigenstates and energy eigenvalues of \(H_0\).

To begin, we know the complete set of eigenstates and eigenvalues for the system Hamiltonian

\[H _ {0} | n \rangle = E _ {n} | n \rangle \label{2.46}\]

The state of the system can then be expressed as a superposition of these eigenstates:

\[| \psi (t) \rangle = \sum _ {n} c _ {n} (t) | n \rangle \label{2.47}\]

The TDSE can be used to find an equation of motion for the eigenstate coefficients

\[c _ {k} (t) = \langle k | \psi (t) \rangle \label{2.48}\]

Starting with

\[\frac {\partial | \psi \rangle} {\partial t} = \frac {- i} {\hbar} H | \psi \rangle \label{2.49}\]

\[\frac {\partial c _ {k} (t)} {\partial t} = - \frac {i} {\hbar} \langle k | H | \psi (t) \rangle \label{2.50}\]

and from Equation \ref{2.47}

\[\frac {\partial c _ {k} (t)} {\partial t} = - \frac {i} {\hbar} \sum _ {n} \langle k | H | n \rangle c _ {n} (t) \label{2.51}\]

Already we see that the time evolution amounts to solving a set of coupled linear ordinary differential equations. These are rate equations with complex rate constants, which describe the feeding of one state into another. Substituting Equation \ref{2.45} we have:

\[\left.\begin{aligned} \frac {\partial c _ {k} (t)} {\partial t} & = - \frac {i} {\hbar} \sum _ {n} \left\langle k \left| \left( H _ {0} + V (t) \right) \right| n \right\rangle c _ {n} (t) \\ & = - \frac {i} {\hbar} \sum _ {n} \left[ E _ {n} \delta _ {k n} + V _ {k n} (t) \right] c _ {n} (t) \end{aligned} \right. \label{2.52}\]

or \(\frac {\partial c _ {k} (t)} {\partial t} + \frac {i} {\hbar} E _ {k} c _ {k} (t) = - \frac {i} {\hbar} \sum _ {n} V _ {k n} (t) c _ {n} (t) \label{2.53}\)

Next, we define and substitute

\[c _ {m} (t) = e^{- i E _ {m} t / h} b _ {m} (t) \label{2.54}\]

which implies a definition for the wavefunction as

\[| \psi (t) \rangle = \sum _ {n} b _ {n} (t) e^{- i E _ {n} t / h} | n \rangle \label{2.55}\]

This defines a slightly different complex amplitude, that allows us to simplify things considerably. Notice that

\[\left| b _ {k} (t) \right|^{2} = \left| c _ {k} (t) \right|^{2}.\]

Also, \(b _ {k} ( 0 ) = c _ {k} ( 0 )\). In practice what we are doing is pulling out the “trivial” part of the time evolution, the time-evolving phase factor, which typically oscillates much faster than the changes to the amplitude of \(b\) or \(c\).

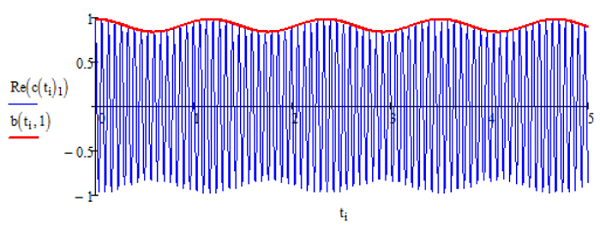
We will come back to this strategy which we discuss the interaction picture.

Now Equation \ref{2.53} becomes

\[e^{- i E _ {t} t / h} \frac {\partial b _ {k}} {\partial t} = - \frac {i} {\hbar} \sum _ {n} V _ {k n} (t) e^{- i E _ {n} t / h} b _ {n} (t) \label{2.56}\]

or \(i \hbar \frac {\partial b _ {k}} {\partial t} = \sum _ {n} V _ {k n} (t) e^{- i \omega _ {n k} t} b _ {n} (t) \label{2.57}\)

This equation is an exact solution. It is a set of coupled differential equations that describe how probability amplitude moves through eigenstates due to a time-dependent potential. Except in simple cases, these equations cannot be solved analytically, but it is often straightforward to integrate numerically.

When can we use the approach described here? Consider partitioning the full Hamiltonian into two components, one that we want to study \(H_0\) and the remaining degrees of freedom \(H_1\). For each part, we have knowledge of the complete eigenstates and eigenvalues of the Hamiltonian: \(H _ {i} | \psi _ {i , n} \rangle = E _ {i , n} | \psi _ {i , n} \rangle\). These subsystems will interact with one another through \(H_{int}\). If we are careful to partition this in such a way that Hint is small compared \(H_0\) and \(H_1\), then it should be possible to properly describe the state of the full system as product states in the subsystems: \(| \psi \rangle = | \psi _ {0} \psi _ {1} \rangle\). Further, we can write a time-dependent Schrödinger equation for the motion of each subsystem as:

\[i \hbar \frac {\partial | \psi _ {1} \rangle} {\partial t} = H _ {1} | \psi _ {1} \rangle \label{2.58}\]

Within these assumptions, we can write the complete time-dependent Schrödinger equation in terms of the two sub-states:

\[i \hbar | \psi _ {0} \rangle \frac {\partial | \psi _ {1} \rangle} {\partial t} + i \hbar | \psi _ {1} \rangle \frac {\partial | \psi _ {0} \rangle} {\partial t} = | \psi _ {0} \rangle H _ {1} | \psi _ {1} \rangle + | \psi _ {1} \rangle H _ {0} | \psi _ {0} \rangle + H _ {\mathrm {int}} | \psi _ {0} \rangle | \psi _ {1} \rangle \label{2.59}\]

Then left operating by \(\langle \psi _ {1} |\) and making use of Equation \ref{2.58}, we can write

\[i \hbar \frac {\partial | \psi _ {0} \rangle} {\partial t} = \left[ H _ {0} + \left\langle \psi _ {1} \left| H _ {\mathrm {int}} \right| \psi _ {1} \right\rangle \right] | \psi _ {0} \rangle \label{2.60}\]

This is equivalent to the TDSE for a Hamiltonian of form (Equation \ref{2.45}) where the external interaction \(V (t) = \left\langle \psi _ {1} \left| H _ {\mathrm {int}} (t) \right| \psi _ {1} \right\rangle\) comes from integrating the 1-2 interaction over the sub-space of \(| \psi _ {1} \rangle\). So this represents a time-dependent mean field method.

Readings

1. Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Quantum Mechanics. Wiley-Interscience: Paris, 1977; p. 308.
2. Merzbacher, E., Quantum Mechanics. 3rd ed.; Wiley: New York, 1998; Ch. 14.
3. Nitzan, A., Chemical Dynamics in Condensed Phases. Oxford University Press: New York, 2006; Sec. 2.3.
4. Sakurai, J. J., Modern Quantum Mechanics, Revised Edition. Addison-Wesley: Reading, MA, 1994; Ch. 2.