1.24: Molecular Vibrations
- Page ID
- 9347
Vibrational motion in diatomic molecules is often discussed within the context of the simple harmonic oscillator in quantum mechanics. A diatomic molecule has only a single bond that can vibrate; we say it has a single vibrational mode. As you may expect, the vibrational motions of polyatomic molecules are much more complicated than those in a diatomic. Firstly, there are more bonds that can vibrate; and secondly, in addition to stretching vibrations, the only type of vibration possible in a diatomic, we can also have bending and torsional vibrational modes. Since changing one bond length in a polyatomic will often affect the length of nearby bonds, we cannot consider the vibrational motion of each bond in isolation; instead we talk of normal modes involving the concerted motion of groups of bonds. As a simple example, the normal modes of a linear triatomic molecule are shown below.

Once we know the symmetry of a molecule at its equilibrium structure, group theory allows us to predict the vibrational motions it will undergo using exactly the same tools we used above to investigate molecular orbitals. Each vibrational mode transforms as one of the irreducible representations of the molecule’s point group. Before moving on to an example, we will quickly review how to determine the number of vibrational modes in a molecule.
Molecular degrees of freedom – determining the number of normal vibrational modes
An atom can undergo only translational motion, and therefore has three degrees of freedom corresponding to motion along the \(x\), \(y\), and \(z\) Cartesian axes. Translational motion in any arbitrary direction can always be expressed in terms of components along these three axes. When atoms combine to form molecules, each atom still has three degrees of freedom, so the molecule as a whole has \(3N\) degrees of freedom, where \(N\) is the number of atoms in the molecule. However, the fact that each atom in a molecule is bonded to one or more neighboring atoms severely hinders its translational motion, and also ties its motion to that of the atoms to which it is attached. For these reasons, while it is entirely possible to describe molecular motions in terms of the translational motions of individual atoms (we will come back to this in the next section), we are often more interested in the motions of the molecule as a whole. These may be divided into three types: translational; rotational and vibrational.
Just as for an individual atom, the molecule as a whole has three degrees of translational freedom, leaving \(3N - 3\) degrees of freedom in rotation and vibration.
The number of rotational degrees of freedom depends on the structure of the molecule. In general, there are three possible rotational degrees of freedom, corresponding to rotation about the \(x\), \(y\), and \(z\) Cartesian axes. A non-linear polyatomic molecule does indeed have three rotational degrees of freedom, leaving \(3N - 6\) degrees of freedom in vibration (i.e \(3N - 6\) vibrational modes). In a linear molecule, the situation is a little different. It is generally accepted that to be classified as a true rotation, a motion must change the position of one or more of the atoms. If we define the \(z\) axis as the molecular axis, we see that spinning the molecule about the axis does not move any of the atoms from their original position, so this motion is not truly a rotation. Consequently, a linear molecule has only two degrees of rotational freedom, corresponding to rotations about the \(x\) and \(y\) axis. This type of molecule has \(3N - 5\) degrees of freedom left for vibration, or \(3N - 5\) vibrational modes.
In summary:
- A linear molecule has \(3N - 5\) vibrational modes
- A non-linear molecule has \(3N - 6\) vibrational modes.
Determining the Symmetries of Molecular Motions
We mentioned above that the procedure for determining the normal vibrational modes of a polyatomic molecule is very similar to that used in previous sections to construct molecular orbitals. In fact, virtually the only difference between these two applications of group theory is the choice of basis set.
As we have already established, the motions of a molecule may be described in terms of the motions of each atom along the \(x\), \(y\) and \(z\) axis. Consequently, it probably won’t come as too much of a surprise to discover that a very useful basis for describing molecular motions comprises a set of \(\begin{pmatrix} x, y, z \end{pmatrix}\) axes centered on each atom. This basis is usually known as the \(\textit{3N}\) Cartesian basis (since there are \(3N\) Cartesian axes, \(3\) axes for each of the \(N\) atoms in the molecule). Note that each molecule will have a different \(3N\) Cartesian basis, just as every molecule has a different atomic orbital basis.
Our first task in investigating motions of a particular molecule is to determine the characters of the matrix representatives for the \(3N\) Cartesian basis under each of the symmetry operations in the molecular point group. We will use the \(H_2O\) molecule, which has \(C_{2v}\) symmetry, as an example.
\(H_2O\) has three atoms, so the \(3N\) Cartesian basis will have \(9\) elements. The basis vectors are shown in the diagram below.
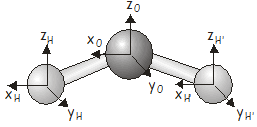
One way of determining the characters would be to construct all of the matrix representatives and take their traces. While you are more than welcome to try this approach if you want some practice at constructing matrix representatives, there is an easier way. Recall that we can also determine the character of a matrix representative under a particular symmetry operation by stepping through the basis functions and applying the following rules:
- Add \(1\) to the character if the basis function is unchanged by the symmetry operation;
- Add \(-1\) to the character if the basis function changes sign under the symmetry operation;
- Add \(0\) to the character if the basis function moves when the symmetry operation is applied.
For \(H_2O\), this gives us the following characters for the \(3N\) Cartesian basis (check that you can obtain this result using the rules above and the basis vectors as drawn in the figure):
\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 9 & -1 & 3 & 1 \end{array} \tag{24.1}\]
There is an even quicker way to work out the characters of the \(3N\) Cartesian basis if you have a character table in front of you. The character for the Cartesian basis is simply the sum of the characters for the \(x\), \(y\), and \(z\) (or \(T_x\), \(T_y\), and \(T_z\)) functions listed in the character table. To get the character for the \(\textit{3N}\) Cartesian basis, simply multiply this by the number of atoms in the molecule that are unshifted by the symmetry operation.
The \(C_{2v}\) character table is shown below.
\[\begin{array}{l|cccc|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & h = 4 \\ \hline A_1 & 1 & 1 & 1 & 1 & z, x^2, y^2, z^2 \\ A_2 & 1 & 1 & -1 & -1 & xy, R_z \\ B_1 & 1 & -1 & 1 & -1 & x, xz, R_y \\ B_2 & 1 & -1 & -1 & 1 & y, yz, R_x \\ \hline \end{array} \tag{24.2}\]
\(x\) transforms as \(B_1\), \(y\) as \(B_2\), and \(z\) as \(A_1\), so the characters for the Cartesian basis are
\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 3 & -1 & 1 & 1 \end{array} \tag{24.3}\]
We multiply each of these by the number of unshifted atoms (\(3\) for the identity operation, \(1\) for \(C_2\), \(3\) for \(\sigma_v\) and \(1\) for \(\sigma_v'\)) to obtain the characters for the \(3N\) Cartesian basis.
\[\begin{array}{lcccc} \chi_{3N}: & 9 & -1 & 3 & 1 \end{array} \tag{24.4}\]
Reassuringly, we obtain the same characters as we did previously. Which of the three methods you use to get to this point is up to you.
We now have the characters for the molecular motions (described by the \(3N\) Cartesian basis) under each symmetry operation. At this point, we want to separate these characters into contributions from translation, rotation, and vibration. This turns out to be a very straightforward task. We can read the characters for the translational and rotational modes directly from the character table, and we obtain the characters for the vibrations simply by subtracting these from the \(3N\) Cartesian characters we’ve just determined. The characters for the translations are the same as those for \(\chi_{Cart}\). We find the characters for the rotations by adding together the characters for \(R_x\), \(R_y\), and \(R_z\) from the character table (or just \(R_x\) and \(R_y\) if the molecule is linear). For \(H_2O\), we have:
\[\begin{array}{lcccc} \text{Operation:} & E & C_2 & \sigma_v(xz) & \sigma_v'(yz) \\ \chi_{3N}: & 9 & -1 & 3 & 1 \\ \chi_{\text{Trans}}: & 3 & -1 & 1 & 1 \\ \chi_{\text{Rot}}: & 3 & -1 & -1 & -1 \\ \chi_{\text{Vib}} = \chi_{3N} - \chi_{\text{Trans}} - \chi_{\text{Rot}}: & 3 & 1 & 3 & 1 \end{array} \tag{24.5}\]
The characters in the final row are the sums of the characters for all of the molecular vibrations. We can find out the symmetries of the individual vibrations by using the reduction equation (Equation (15.20)) to determine the contribution from each irreducible representation.
In many cases you won’t even need to use the equation, and can work out which irreducible representations are contributing just by inspection of the character table. In the present case, the only combination of irreducible representations that can give the required values for \(\chi_{\text{Vib}}\) is \(2A_1 + B_1\). As an exercise, you should make sure you are also able to obtain this result using the reduction equation.
So far this may all seem a little abstract, and you probably want to know is what the vibrations of \(H_2O\) actually look like. For a molecule with only three atoms, it is fairly easy to identify the possible vibrational modes and to assign them to the appropriate irreducible representation.
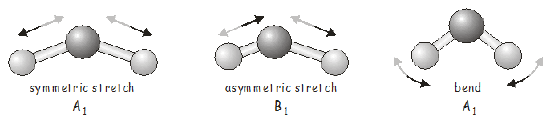
For a larger molecule, the problem may become much more complex, and in that case we can generate the SALCs of the \(3N\) Cartesian basis, which will tell us the atomic displacements associated with each vibrational mode. We will do this now for \(H_2O\).
Atomic displacements using the 3N Cartesian basis
As before, we generate the SALCs of each symmetry by applying the appropriate projection operator to each of the basis functions (or in this case, basis vectors) \(f_i\) in turn.
\[\phi_i = \sum_g \chi_k(g) g f_i \tag{24.6}\]
In this case we have \(9\) basis vectors, which we will label \(x_H\), \(y_H\), \(z_H\), \(x_O\), \(y_O\), \(z_O\), \(x_{H'}\), \(y_{H'}\), \(z_{H'}\), describing the displacements of the two \(H\) atoms and the \(O\) atom along Cartesian axes. For the SALCs of \(A_1\) symmetry, applying the projection operator to each basis vector in turn gives (check that you can obtain this result):
\[\begin{array}{rclll} \phi_1(x_H) & = & x_H - x_{H'} + x_H - x_{H'} & = & 2x_H - 2x_{H'} \\ \phi_2(y_H) & = & y_H - y_{H'} - y_H + y_{H'} & = & 0 \\ \phi_3(z_H) & = & z_H + z_{H'} + z_H + z_{H'} & = & 2z_H + 2z_{H'} \\ \phi_4(x_O) & = & x_O - x_O + x_O - x_O & = & 0 \\ \phi_5(y_O) & = & y_O - y_O - y_O + y_O & = & 0 \\ \phi_6(z_O) & = & z_O + z_O + z_O + z_O & = & 4z_O \\ \phi_7(x_{H'}) & = & x_{H'} - x_H + x_{H'} - x_H & = & 2x_{H'} - 2x_H \\ \phi_8(y_{H'}) & = & y_{H'} - y_H - y_{H'} + y_H & = & 0 \\ \phi_9(z_{H'}) & = & z_{H'} + z_H + z_{H'} + z_H & = & 2z_{H'} + 2z_H \end{array} \tag{24.7}\]
We see that the motion characteristic of an \(A_1\) vibration (which we have identified as the symmetric stretch and the bending vibration) may be summarized as follows:
- \(2(x_H - x_{H'})\) - the two hydrogen atoms move in opposite directions along the \(x\) axis.
- \(2(z_H + z_{H'})\) - the two hydrogen atoms move in the same direction along the \(z\) axis.
- \(4z_O\) - the oxygen atom moves along the \(z\) axis.
- There is no motion of any of the atoms in the \(y\) direction.
The asymmetric stretch has \(B_1\) symmetry, and applying the projection operator in this case gives:
\[\begin{array}{rclll} \phi_1(x_H) & = & x_H + x_{H'} + x_H + x_{H'} & = & 2x_H + 2x_{H'} \\ \phi_2(y_H) & = & y_H + y_{H'} - y_H - y_{H'} & = & 0 \\ \phi_3(z_H) & = & z_H - z_{H'} + z_H - z_{H'} & = & 2z_H - 2z_{H'} \\ \phi_4(x_O) & = & x_O + x_O + x_O + x_O & = & 4x_O \\ \phi_5(y_O) & = & y_O + y_O - y_O - y_O & = & 0 \\ \phi_6(z_O) & = & z_O - z_O + z_O - z_O & = & 0 \\ \phi_7(x_{H'}) & = & x_{H'} + x_H + x_{H'} + x_H & = & 2x_{H'} + 2x_H \\ \phi_8(y_{H'}) & = & y_{H'} + y_H - y_{H'} - y_H & = & 0 \\ \phi_(z_{H'}) & = & z_{H'} - z_H + z_{H'} - z_H & = & 2z_{H'} - 2z_H \end{array} \tag{24.8}\]
In this vibrational mode, the two \(H\) atoms move in the same direction along the \(x\) axis and in opposite directions along the \(z\) axis.
We have now shown how group theory may be used together with the \(3N\) Cartesian basis to identify the symmetries of the translational, rotational and vibrational modes of motion of a molecule, and also to determine the atomic displacements associated with each vibrational mode.
Molecular vibrations using internal coordinates
While it was fairly straightforward to investigate the atomic displacements associated with each vibrational mode of \(H_2O\) using the \(3N\) Cartesian basis, this procedure becomes more complicated for larger molecules. Also, we are often more interested in how bond lengths and angles change in a vibration, rather than in the Cartesian displacements of the individual atoms. If we are only interested in looking at molecular vibrations, we can use a different procedure from that described above, and start from a basis of internal coordinates. Internal coordinates are simply a set of bond lengths and bond angles, which we can use as a basis for generating representations and, eventually, SALCs. Since bond lengths and angles do not change during translational or rotational motion, no information will be obtained on these types of motion.
For \(H_2O\), the three internal coordinates of interest are the two \(OH\) bond lengths, which we will label \(r\) and \(r'\), and the \(HOH\) bond angle, which we will label \(\theta\). If we wanted to, we could separate our basis into two different bases, one consisting only of bond lengths, to describe stretching vibrations, and one consisting of only bond angles, to describe bending vibrations. However, the current example is simple enough to treat all the basis functions together.
As usual, our first step is to work out the characters of the matrix representatives for this basis under each symmetry operation. The effects of the various transformations on our chosen basis, and the characters of the corresponding representatives, are:
\[\begin{array}{lc} E(r, r', \theta) = (r, r', \theta) & \chi(E) = 3 \\ C_2(r, r', \theta) = (r', r, \theta) & \chi(C_2) = 1 \\ \sigma_v(xz)(r, r', \theta) = (r, r', \theta) & \chi(\sigma_v) = 3 \\ \sigma_v'(yz)(r, r', \theta) = (r', r, \theta) & \chi(\sigma_v') = 1 \end{array} \tag{24.9}\]
These are the same characters as we found before using the \(3N\) Cartesian basis, and as before, we can see by inspection of the character table that the representation may be reduced down to the sum of irreducible representations \(2A_1 + B_1\). We can now work out the symmetry adapted linear combinations of our new basis set to see how the bond lengths and angle change as \(H_2O\) vibrates in each of the three vibrational modes.
Again, we will use the projection operator \(\phi_i = \Sigma_g \chi_k(g) g f_i\) applied to each basis function in turn.
Firstly, the \(A_1\) vibrations:
\[\begin{array}{rclll} \phi_1(r) & = & r + r' + r + r' & = & 2(r + r') \\ \phi_2(r') & = & r' + r + r' + r & = & 2(r' + r) \\ \phi_3(\theta) & = & \theta + \theta + \theta + \theta & = & 4\theta \end{array} \tag{24.10}\]
From these SALCs, we can identify \(\phi_1\) (and \(\phi_2\), which is identical) with the symmetric stretch, in which both bond lengths change in phase with each other, and \(\phi_3\) with the bend.
Now for the \(B_1\) vibration:
\[\begin{array}{rclll} \phi_4(r) & = & r - r' + r - r' & = & 2(r - r') \\ \phi_5(r') & = & r' - r + r' - r & = & 2(r' - r) \\ \phi_6(\theta) & = & \theta - \theta + \theta - \theta & = & 0 \end{array} \tag{24.11}\]
\(\phi_4\) and \(\phi_5\) are not linearly independent, and either one may be chosen to describe the asymmetric stretch, in which one bond lengthens as the other shortens.
Note: When using internal coordinates, it is important that all of the coordinates in the basis are linearly independent. If this is the case then the number of internal coordinates in the basis will be the same as the number of vibrational modes (\(3N - 5\) or \(3N - 6\), depending on whether the molecule is linear or non-linear). This requirement is satisfied in the \(H_2O\) example above. For a less straightforward example, consider the methane molecule, \(CH_4\). It might appear that we could choose a basis made up of the four \(C\)-\(H\) bond lengths and the six \(H\)-\(C\)-\(H\) bond angles. However, this would give us \(10\) basis functions, and \(CH_4\) has only \(9\) vibrational modes. This is due to the fact that the bond angles are not all independent of each other. It can be tricky to come up with the appropriate internal coordinate basis to describe all of the molecular motions, but all is not lost. Even if you can’t work out the appropriate bond angles to choose, you can always take a basis of bond lengths to investigate the stretching vibrations of a molecule. If you want to know the symmetries of the bending vibrations, you can use the \(3N\) Cartesian basis method to determine the symmetries of all of the vibrational modes and compare these with the stretching mode symmetries to identify the bending modes.
Contributors and Attributions
Claire Vallance (University of Oxford)


