3.5: Applications - Kinetics of Catalytic Reactions
- Page ID
- 25377
It is possible to predict how the kinetics of certain heterogeneously-catalyzed reactions might vary with the partial pressures of the reactant gases above the catalyst surface by using the Langmuir isotherm expression for equilibrium surface coverages.
Unimolecular Decomposition
Consider the surface decomposition of a molecule A, i.e. the process
\[A_{(g)} \rightleftharpoons A_{(ads)} → Products\]
Let us assume that:
- The decomposition reaction occurs uniformly across the surface sites at which molecule A may be adsorbed and is not restricted to a limited number of special sites.
- The products are very weakly bound to the surface and, once formed, are rapidly desorbed.
- The rate determining step (rds) is the surface decomposition step.
Under these circumstances, the molecules of A adsorbed on the surface are in equilibrium with those in the gas phase and we may predict the surface concentration of A from the Langmuir isotherm, i.e.
\[θ = \dfrac{bP}{1 + bP}\]
The rate of the surface decomposition (and hence of the reaction) is given by an expression of the form
\[rate = k θ\]
This is assuming that the decomposition of A(ads) occurs in a simple unimolecular elementary reaction step and that the kinetics are first order with respect to the surface concentration of this adsorbed intermediate). Substituting for the coverage, θ, gives us the required expression for the rate in terms of the pressure of gas above the surface
\[rate = \dfrac{k b P}{1 + b P} \label{rate}\]
It is useful to consider two extremes:
Low Pressure/Binding Limit
This is the low pressure (or weak binding. i.e., small \(b\)) limit: under these conditions the steady state surface coverage, \(θ\), of the reactant molecule is very small.
\[b P \ll 1\]
then
\[1 + bP \approx 1\]
and Equation \(\ref{rate}\) can be simplified to
\[rate \approx kbP\]
Under this limiting case, the kinetics follow a first order reaction (with respect to the partial pressure of \(A\)) with an apparent first order rate constant \(k' = kb\).
High Pressure/Binding Limit
This is the high pressure (or strong binding, i.e., large \(b\)) limit: under these conditions the steady state surface coverage, \(θ\), of the reactant molecule is almost unity and
\[bP \gg 1\]
then
\[1 + bP \approx bP\]
and Equation \(\ref{rate}\) can be simplified to
\[rate \approx k\]
under this limiting case, the kinetics follow a zero order reaction (with respect to the partial pressure of \(A\)). The rate shows the same pressure variation as does the surface coverage, but this hardly surprising since it is directly proportional to θ.
These two limiting cases can be identified in the general kinetics from Equation \(\ref{rate}\) in Figure 3.5.1.
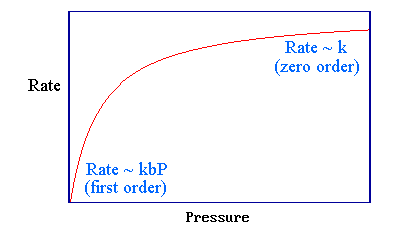
Figure 3.5.1:
Bimolecular Reaction (between molecular adsorbates)
Consider a Langmuir-Hinshelwood reaction of the following type:
\[A_{(g)} \rightleftharpoons A_{(ads)} \label{Eq2.1}\]
\[B_{(g)} \rightleftharpoons B_{(ads)} \label{Eq2.2} \]
\[A_{(ads)} + B_{(ads)} \overset{slow}{\longrightarrow} AB_{(ads)} \overset{fast}{\longrightarrow} AB_{(g)} \label{Eq2.3} \]
We will further assume, as noted in the above scheme, that the surface reaction between the two adsorbed species (left side of Equation \(\ref{Eq2.3}\) is the rate determining step.
If the two adsorbed molecules are mobile on the surface and freely intermix then the rate of the reaction will be given by the following rate expression for the bimolecular surface combination step
\[Rate = k θ_A θ_B\]
For a single molecular adsorbate the surface coverage (as given by the standard Langmuir isotherm) is
\[ θ = \dfrac{bP}{1 + bP}\]
Where two molecules (\(A\) & \(B\) ) are competing for the same adsorption sites then the relevant expressions are (see derivation):
\[\theta_A = \dfrac{b_AP_A}{1+b_AP_A + b_BP_B}\]
and
\[\theta_B = \dfrac{b_BP_B}{1+b_AP_A + b_BP_B}\]
Substituting these into the rate expression gives:
\[Rate = k \theta_A \theta_B = \dfrac{k b_AP_A b_BP_B }{( 1+b_AP_A + b_BP_B )^2}\]
Once again, it is interesting to look at several extreme limits
Low Pressure/Binding Limit
\[b_A P_A \ll 1\]
and
\[b_B P_B \ll 1\]
In this limit that \(θ_A\) & \(θ_B\) are both very low, and
\[rate → k b_A P_A b_B P_B = k' P_A P_B\]
i.e. first order in both reactants
Mixed Pressure/Binding Limit
\[b_A P_A \ll 1 \ll b_B P_B\]
In this limit \(θ_A → 0\), \(θ_B → 1\), and
\[Rate → \dfrac{k b_A P_A }{b_B P_B } = \dfrac{k' P_A}{P_B}\]
i.e. first order in \(A\), but negative first order in \(B\)
Clearly, depending upon the partial pressure and binding strength of the reactants, a given model for the reaction scheme can give rise to a variety of apparent kinetics: this highlights the dangers inherent in the reverse process - namely trying to use kinetic data to obtain information about the reaction mechanism.
On precious metal surfaces (e.g. Pt), the \(CO\) oxidation reaction is generally believed to by a Langmuir-Hinshelwood mechanism of the following type:
\[CO_{(g)} \rightleftharpoons CO_{(ads)}\]
\[O_{2 (g)} \rightleftharpoons 2 O_{(ads)}\]
\[CO_{(ads)} + O_{(ads)} \overset{slow}{\longrightarrow} CO_{2 (ads)} \overset{fast}{\longrightarrow} CO_{2 (g)}\]
As CO2 is comparatively weakly-bound to the surface, the desorption of this product molecule is relatively fast and in many circumstances it is the surface reaction between the two adsorbed species that is the rate determining step.
If the two adsorbed molecules are assumed to be mobile on the surface and freely intermix then the rate of the reaction will be given by the following rate expression for the bimolecular surface combination step
\[Rate = k \,θ_{CO}\, θ_O\]
Where two such species (one of which is molecularly adsorbed, and the other dissociatively adsorbed) are competing for the same adsorption sites then the relevant expressions are (see derivation):
\[\theta_{CO} = \dfrac{b_{CO}P_{CO}}{1+ \sqrt{b_OP_{O_2}} + b_{CO}P_{CO}}\]
and
\[\theta_{O} = \dfrac{ \sqrt{b_OP_{O_2}} }{1+ \sqrt{b_OP_{O_2}} + b_{CO}P_{CO}}\]
Substituting these into the rate expression gives:
\[rate = k \theta_{CO} \theta_O = \dfrac{ k b_{CO}P_{CO} \sqrt{b_OP_{O_2}} }{(1+ \sqrt{b_OP_{O_2}} + b_{CO}P_{CO})^2} \label{Ex1.1}\]
Once again, it is interesting to look at certain limits. If the \(CO\) is much more strongly bound to the surface such that
\[b_{CO}P_{CO} \gg 1 + \sqrt{b_OP_{O_2}}\]
then
\[1 + \sqrt{b_OP_{O_2}} + b_{CO}P_{CO} \approx b_{CO}P_{CO}\]
and the Equation \(\ref{Ex1.1}\) simplifies to give
\[rate \approx \dfrac{k \sqrt{b_OP_{O_2}} } {b_{CO}P_{CO}} = k' \dfrac{P^{1/2}_{O_2}}{P_{CO}}\]
In this limit the kinetics are half-order with respect to the gas phase pressure of molecular oxygen, but negative order with respect to the \(CO\) partial pressure, i.e. \(CO\) acts as a poison (despite being a reactant) and increasing its pressure slows down the reaction. This is because the CO is so strongly bound to the surface that it blocks oxygen adsorbing, and without sufficient oxygen atoms on the surface the rate of reaction is reduced.


