11.1.4: The Continuous Limit
- Page ID
- 5268
In taking the limit \(P\rightarrow \infty \), it will prove useful to define a parameter
\[\varepsilon = {\beta\hbar \over P} \nonumber \]
so that \(P\rightarrow \infty \) implies \(\varepsilon\rightarrow 0\). In terms of \(\varepsilon \), the partition function becomes
\[Q(\beta) = \lim_{P\rightarrow\infty ,\varepsilon\rightarrow 0} \left ( {m \over 2 \pi \varepsilon \hbar } \right ) ^{P/2} \int dx_1 \cdots dx_P exp \left [ -{\varepsilon \over \hbar } \sum _{i=1}^P \left ( {m \over 2} \left ( {x_{i+1} - x_i \over \varepsilon } \right ) ^2 + U(x_i)\right)\right] \vert _{x_{P+1}=x_1} \nonumber \]
We can think of the points \( {x_1,...,x_P} \) as specific points of a continuous functions \(x(\tau) \), where
\[x_k = x(\tau=(k-1)\varepsilon) \nonumber \]
such that \( x(0)=x(\tau=P\varepsilon)=x(\tau=\beta\hbar) \):

Note that
\[ \lim_{\varepsilon\rightarrow 0} \left({x_{k+1}-x_k \over \varepsilon } \right) = \lim_{\varepsilon \rightarrow 0} \left ( x(k\varepsilon) - x (( k -1) \varepsilon ) \over \varepsilon \right) = {dx \over d\tau } \nonumber \]
and that the limit
\[ \lim_{P\rightarrow\infty ,\varepsilon\rightarrow 0} {\varepsilon \over \hbar } \sum _{i=1}^P \left [ {m \over 2} \left({x_{i+1}-x_i \over \varepsilon}\right)^2 + U(x_i)\right] \nonumber \]
is just a Riemann sum representation of the continuous integral
\[ {1 \over \hbar}\vert\int_0^{\beta\hbar}d\tau\left[{m\over 2}\left({dx \over d\tau}\right)^2+ U(x(\tau))\right] \nonumber \]
Finally, the measure
\[ \lim_{P\rightarrow\infty ,\varepsilon\rightarrow 0}\left({m \over 2\pi\varepsilon\hbar^2}\right)^{P/2}dx_1\cdots dx_P \nonumber \]
represents an integral overa all values that the function \(x(\tau)\) can take on between \(\tau = 0 \) and \(\tau = \beta \hbar \) such that \(x (0) = x (\beta \hbar ) \). We write this symbolically as \({\cal D}x(\cdot ) \). Therefore, the \(P \rightarrow \infty \) limit of the partition function can be written as
\[\begin{align*} Q (\beta ) &=\int\; dx\int_{x(0)=x}^{x(\beta\hbar)=x} {\cal D}x(\cdot) exp\left [ - {1 \over \hbar} \int_0^{\beta\hbar}d\tau\left({m \over 2}\dot{x}^2 + U(x(\tau))\right)\right] \\[4pt] &= \oint {\cal D}x(\cdot)\exp\left[-{1 \over \hbar}\int_0^{\beta\hbar}d\tau\left({m \over 2}\dot{x}^2 + U(x(\tau))\right)\right] \end{align*} \]
The above expression in known as a functional integral. It says that we must integrate over all functions (i.e., all values that an arbitrary function \(x(\tau)\) may take on) between the values \(\tau = 0\) and \(\tau = \beta \hbar \). It must really be viewed as the limit of the discretized integral introduced in the last lecture. The integral is also referred to as a path integral because it implies an integration over all paths that a particle might take between \(\tau = 0\) and \(\tau = \beta \hbar \) such that \(x (0) = x (\beta \hbar \), where the paths are parameterized by the variable \(\tau\) (which is not time!). The second line in the above expression, which is equivalent to the first, indicates that the integration is taken over all paths that begin and end at the same point, plus a final integration over that point.
The above expression makes it clear how to represent a general density matrix element \( \langle x\vert\exp(-\beta H)\vert x'\rangle \):
\[ \langle x\vert e^{-\beta H}\vert x'\rangle = \int_{x(0)=x}^{x(\beta \hbar) = x'}{\cal D} x (\cdot) exp \left [ - {1 \over \hbar} \int _{0}^{\beta \hbar }d\tau \left({m \over 2}\dot{x}^2 + U(x(\tau))\right)\right] \nonumber \]
which indicates that we must integrate over all functions \(x (\tau)\) that begin at \(x\) at \(\tau = 0 \) and end at \(x'\) at \(\tau = \beta \hbar \):
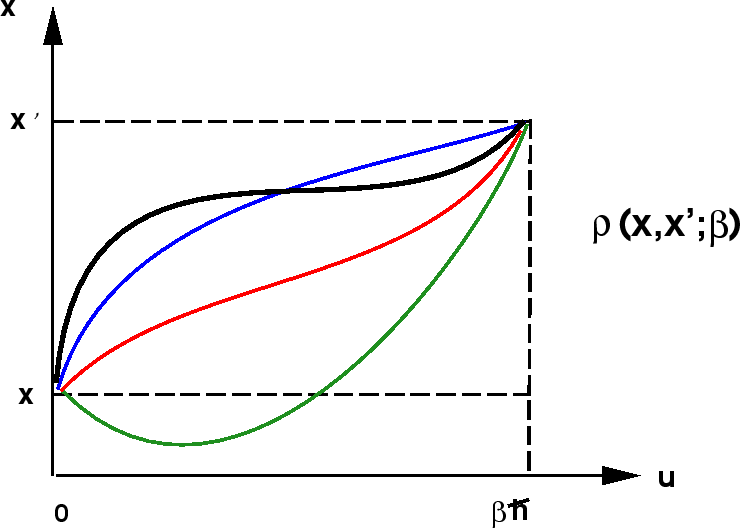
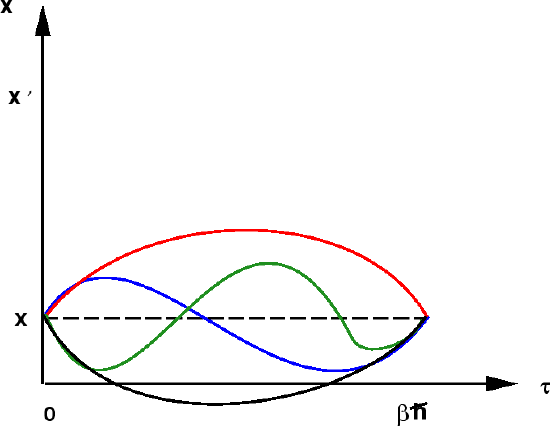
Similarly, diagonal elements of the density matrix, used to compute the partition function, are calculated by integrating over all periodic paths that satisfy \( x(0) = x (\beta \hbar ) = x \):
Note that if we let \(\beta = {it \over \hbar } \), then the density matrix becomes
\[ \rho(x,x';it/\hbar) = \langle x\vert e^{-iHt/\hbar}\vert x'\rangle = U(x,x';t) \nonumber \]
which are the coordinate space matrix elements of the quantum time evolution operator. If we make a change of variables \( { \tau = is } \) in the path integral expression for the density matrix, we find that the quantum propagator can also be expressed as a path integral:
\[ U(x,x';t) = \langle x\vert e^{-iHt/\hbar}\vert x'\rangle = \int _{x(0) = x}^{x(t) = x'} {\cal D} x (\cdot) exp \left [ {i \over \hbar} \int _0^t ds \left ({m \over 2}\dot{x}(s) - U(x(s))\right)\right] \nonumber \]
Such a variable transformation is known as a Wick rotation. This nomenclature comes about by viewing time as a complex quantity. The propagator involves real time, while the density matrix involves a transformation \(t = - \beta \hbar \) to the imaginary time axis. It is because of this that the density matrix is sometimes referred to as an imaginary time path integral.


