7.3: Structure and distribution functions in classical liquids and gases
- Page ID
- 5239
So far, we have developed the classical theory of ensembles and applied it to the ideal gas, for which there was no potential of interaction between the particles: \(U=0\). We were able to derive all the thermodynamics for this system using the various ensembles available to us, and, in particular, we could compute the equation of state. Now, we wish to consider the general case that the potential is not zero. Of course, all of the interesting physics and chemistry of real systems results from the specific interactions between the particles. Real systems can exhibit spatial structure, undergo phase transitions, undergo chemical changes, exhibit interesting dynamics, basically, a wide variety of rich behavior.
Consider the two snapshots below.
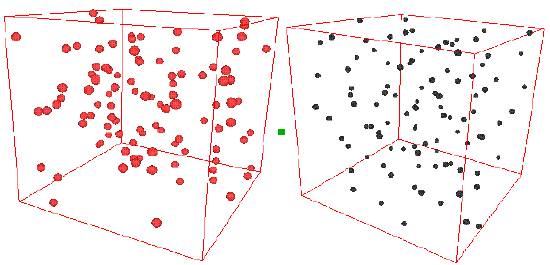
On the left is shown a configuration of an ideal gas, and on the right is shown a configuration of liquid argon. Can you see any inherent structure in the snapshot of liquid argon? While it may not be readily apparent, there is considerable structure in the liquid argon system that is clearly not present in the ideal gas. One way of quantifying spatial structure is through the use of the radial distribution function g(r), which will be discussed in great detail later. For now, it is sufficient to know that g(r) is a measure of the probability that a particle will be located a distance r from a another particle in the system. The figure below shows the function g(r) for the ideal gas and for the liquid argon systems.
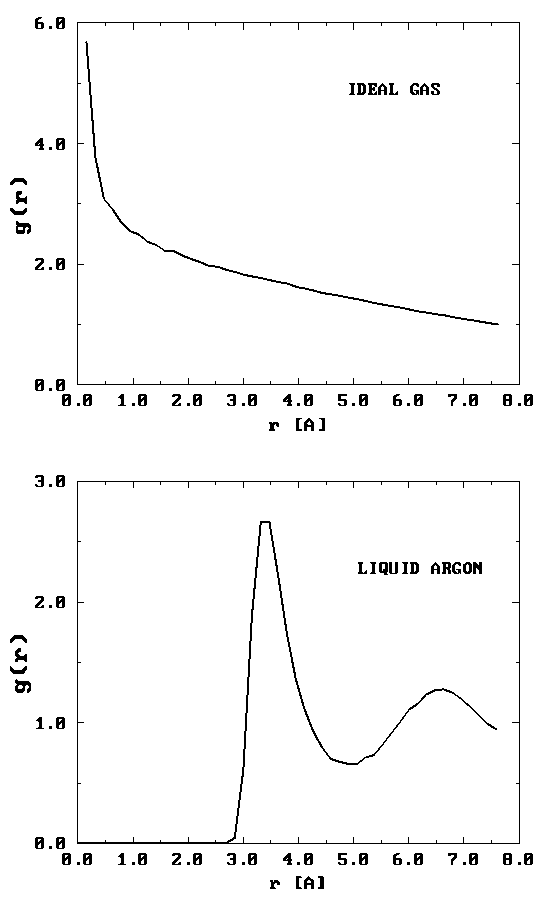
It can be seen that the radial distribution function for the ideal gas is completely featureless signifying that it is equally likely to find a particle at any distance \(r\) from a given particle. (Since the probability is uniform, \(g (r) \sim \frac {1}{r^2} \) for small \(r\). This is the particularly normalization condition on \(g(r)\) that gives rise to uniform probability. Hence its rapidly rising behavior for small \(r\).) For the liquid argon system, \(g(r)\) exhibits several peaks, indicating that at certain radial values, it is more likely to find particles than at others. This is a result of the attractive nature of the interaction at such distances. The plot of \(g(r)\) also shows that there is essentially zero probability of finding particles at distances less than about 2.5 Å from each other. This is due to the presence of very strong repulsive forces at short distances.
Sometimes, the structure can be readily seen in snapshots of configurations. Consider the following snapshot of a system of water molecules:
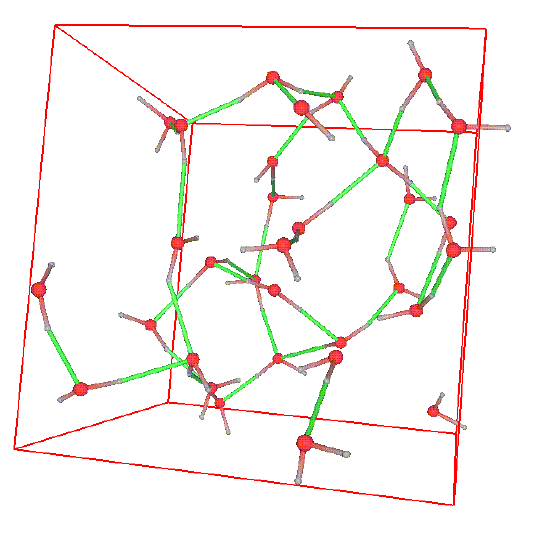
The red spheres are oxygen atoms, the grey spheres are hydrogen atoms, the green lines are hydrogen bonds, and the reddish-grey lines are covalent bonds. A good deal of structure can be seen in the form of a complex network of hydrogen bonds. This high degree of structure is characteristic of water and gives rise to the ease which with water can form stable, organized structures around other molecules. In water, one can ask several questions related to structure. For example, what is the probability that an oxygen atom will be found at a distance \(r\) away from another oxygen atoms? What is the probability that a hydrogen atom will be located at a distance r from an oxygen atom, etc. The plot below shows the radial distribution functions corresponding to these two scenarios.

The peak in the O-O radial distribution function occurs at roughly 2.8Å which is the well known average hydrogen bond length in water. Of course, one could also ask about structure from the point of view of a hydrogen atom and obtain two other representations of structure in water.


