2D NMR Introduction
- Page ID
- 1805
Some general principles and techniques used in two-dimensional NMR are discussed. Applications covered are mostly concerned with protein NMR, but additional 2D techniques and applications can be found in the references section.
Introduction
A two dimensional variation of NMR was first proposed by Jean Jeener in 1971; since then, scientists such as Richard Ernst have applied the concept to develop the many techniques of 2D NMR. Although traditional, one-dimensional NMR is sufficient to observe distinct peaks for the various funtional groups of small molecules, for larger, more complex molecules, many overlapping resonances can make interpretation of an NMR spectrum difficult. Two-dimensional NMR, however, allows one to circumvent this challenge by adding additional experimental variables and thus introducing a second dimension to the resulting spectrum, providing data that is easier to interpret and often more informative.
Basics of 2D NMR
Experimental Set-up
In traditional 1D Fourier transform NMR, a sample under a magnetic field is hit with a series of RF pulses, as seen in the pulse sequence below, and the Fourier transform of the outgoing signal results in a 1D spectra as a function chemical shift.
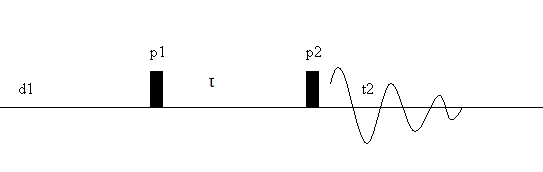
Figure 1: Pulse sequence of a typical FT-NMR experiment
A 2D NMR experiment, however, adds an additional dimension to the spectra by varying the length of time (\(\tau\))) the system is allowed to evolve following the first pulse. The result is an outgoing signal f (\(\tau\), t2), which, when Fourier transformed, gives a 2D spectrum of F (\(\omega\)1, \(\omega\)2).
The use of two-dimensional NMR allows the researcher to better resolve signals which would normally overlap in 1D NMR. Depending on the size of your molecule, different variations or combinations of 2D and multidimensional NMR experiments are utilized.
The Spin Hamiltonian
The spin of a given nuclei during any NMR experiment is governmed by the spin Hamiltonian. If long-range spin interactions are ignored, the spin Hamilitonian for a one-spin system is given the equation
\[\hat{H}=\hat{H}^0+\hat{H}_{RF}\]
The magnetic field along the z-axis, shielding, and J-coupling with nearby nuclei are all constant and are accounted for in H0. HRF is the induced magnetic field resulting from an RF pulse. For a system where two spins are coupled, the H0 is
\[\hat{H}=\omega_{1}^0\hat{I}_{1z}+\omega_{2}^0\hat{I}_{2z}+{2}\pi{J}_{12}\hat{I}_{1}\hat{I}_{2}\]
Where \(\omega\) is the Larmor frequency, I is the net magnetization vector of the given nucleus or nuclei, and J is the observed J coupling between nuclei. \(\omega\) is directly related to the chemical shift (\(\delta\)) by the equation
\[\omega_{j}^0=-\gamma_{j}{B}^0(1+\delta_{j}^{iso})\]
Where \(\gamma\) is the gyromagnetic ratio of the given isotope. If nuclei 1 and 2 are of the same element and isotope, the system is referred to as homonuclear. If they are different, it is a heteronuclear spin system.
Correlation Spectroscopy (COSY)
The most basic form of 2D NMR is the 2D COSY (pulse sequence shown below) experiment, a homonuclear experiment with a pulse sequence similar to the procedure dicussed above. It consists of a 90o RF pusle followed by an evolution time and an additional 90o pulse. The resulting oscillating magnetization (symbolized by decaying the sinusoidal curve) is then acquired during t2.
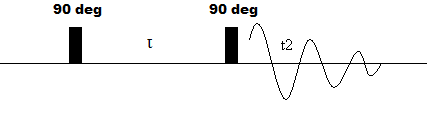
Figure 2: Pulse sequence of a 2D COSY experiment
The analysis of the acquired spectrum is discussed below, making it useful for determining the coupling between nuclei that are connected through one to three bond lengths. However, in macromolecules such as proteins, coupling through bonds alone is not sufficient to obtain substantial structural information. For this reason, the Nuclear Overhauser Effect (NOE) is often used in protein NMR to obtain information on the distance between nuclei through space rather than through bonds.
Nuclear Overhauser Effect (NOE)
Thus far, only the coupling of nuclei through bonds has been considered. In bond coupling, the magnetization of nuclei affect those closely bound to them through the electrons that make up those bonds; however, coupling directly between nuclei that are in close spatial proximity to each other also occurs. This is called the Nuclear Overhauser Effect, and it arises when the spin relaxation of nuclei A is felt by nearby nuclei B, stimulating a corresponding change in magnetization in B. In a typical NMR spectrum, the interference of electrons makes this coupling undetectable. However, a sample can be decoupled to “neutralize” the bond coupling through electrons, allowing the space coupling of the NOE to be detected. This is called NOESY (NOE correlation spectroscopy) and is another type of homonuclear NMR.
The pulse sequence for a NOESY NMR experiment is depicted below.
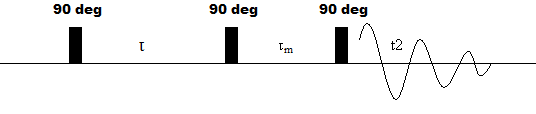
Figure 3: Pulse sequence of NOESY experiment
Like COSY, the first step is a 90o pulse followed by a variable evolution time. Unlike COSY, however, pulse two actually consists of two 90 degree pulses separated by a short delay. The first pulse converts the bulk magnetization from the transverse plane to the z-plane, eliminating the effect of electron-aided bond coupling. Then, during the \(\tau\)m, there is cross relaxation between spatially adjacent nuclei. Finally, the last 90 degree pulse converts the space coupling of nuclei into an observable transverse magnetization, which can be detected during t2.
2D NMR Spectra
As discussed earlier, by performing multiple one dimensional experiments at varying lengths (\(\tau\)) of the evolution period and performing a Fourier transformation on the signal which converts f (\(\tau\), t2) to F(\(\omega\)1, \(\omega\)2), a two dimensional spectrum can be formed into a 3D contour map.
A more useful representation of 2D data is called a correlation map. The correlation map of the steroid progesterone is shown below.
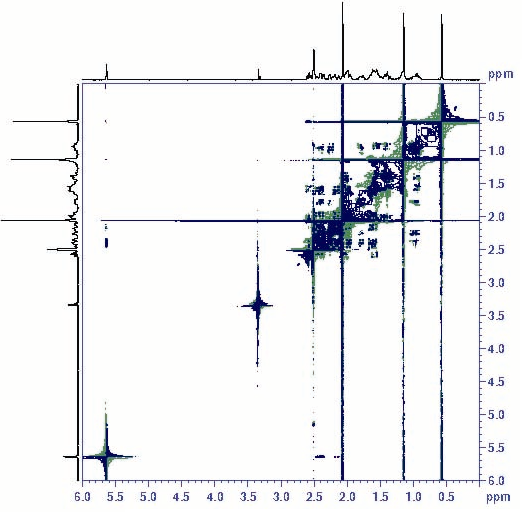
Figure 4: 2D COSY spectrum of progesterone
In this representation, the x- and y-axes correspond to the frequencies resulting from the Fourier transforms, and the intensity of shade at each frequency coordinate indicates the peak intensity. Two types of peaks are observed in a homonuclear correlation map—diagonal peaks and cross peaks. Diagonal peaks are found along the diagonal of the map where the x- and y-axes have equal frequency values and simply correspond to the absorptions from a one-dimensional NMR experiment. Because heteronuclear NMR does not involve the same isotope, diagonal peaks are not observed. Cross peaks, on the other hand, give information on the coupling of two nuclei and are seen in both homo- and heteronuclear spectra.
Applications in Protein NMR
As previously mentioned, the major advantage of 2D NMR over 1D NMR is the ability to distinguish between the overlapping signals that exist in larger molecules. Heteronuclear two-dimensional NMR is especially important in biological chemistry in the elucidation of the three-dimensional structure of proteins.
Heteronuclear Single Quantum Coherence (HSQC)
A protein is make-up of a series of amino acid monomers. Although there are 19 different amino acids each with a distinct side chain, the protein backbone is an invariable pattern of NH-C-CO as shown in Figure 5.
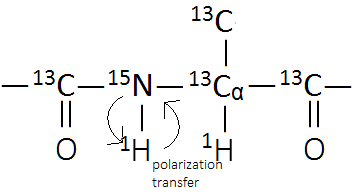
When synthesized under the right conditions, a heavy atom protein can be produced which constains NMR active nuclei; however, a 15N nucleus has a very low gyromagnetic ratio. According to the Hamiltonian operators discussed above, it will give a very weak signal in traditional 2D NMR. Fortunately, the nucleus can be detected indirectly by transferring polarization through a 1H nucleus. This method is used in HSQC NMR.
In protein NMR, each HSQC experiment has three steps:
- An INEPT (insensitive nuclei enhanced by polarization transfer) transfers the polarization of a 1H nuclei to the neighboring 15N (see figure below)
- The polarization is transferred back to the 1H nuclei
- Signal from the 1H nuclei is recorded
The pulse sequence for a typical HSQC experiment is detailed below.
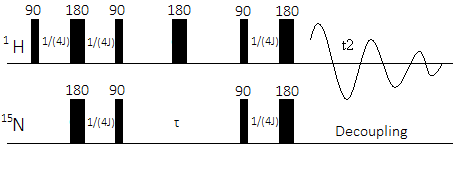
Figure 6: Pulse sequence of a HSQC experiment involving 1H and 15N nuclei
A 90o1H RF pulse creates a transverse polarization in 1H nuclei. Following the pulse, the nuclei are allowed to evolve for a 1/(4J) time period, which is the longitudinal relaxation time. Next, a 180o 1H and 15N pulse are used at the same time. During the subsequent relaxation time, the 1H nuclei develop a polarization that is antiphase to 15N. Finally, a 90o 1H and 15N pulse, again simultaneous, enacts the INEPT transfer of antiphase magnetization from the 1H nucleus to the 15N nucleus. Following the INEPT transfer, the 15N nuclei are allowed to evolve during \(\tau\)before a reverse INEPT transfer moves the 15N polarization back to 1H and a 15N decoupled signal is recorded.
An example HSCQ spectrum from ubiquitin is shown below.
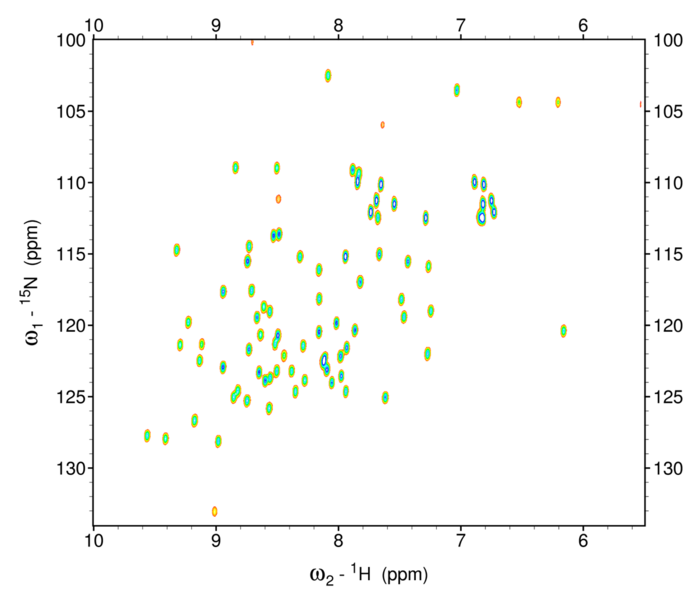
Figure 7: 1H15N HSQC spectrum of ubiquitin
Notice the greater clarity of spectra of the HSQC vs the COSY experiment. This is a strong advantage of heteronuclear NMR. In this diagram, each peak corresponds to a cross peak, showing coupling between sets of 1H and 15N nuclei. Each peak represents the 15N—1H of a unique amino acid along the backbone of the amino acid.
The 2D HSQC experiment which relates 1H and 15N is just the start on the long, complicated road of protein structural characterization using 2D and multidimensional NMR techniques. The next experiment is typically a 3D NMR technique in which coupling with 13C is also including in the spectra—which will give information on which NH peaks are associated with which type of amino acid residue—followed by a NOE experiment—which gives spatial distances between nuclei. These multidimensional techniques are outside the scope of this module; however, the principles which were applied in the construction and analysis of the 2D spectra can be carried over to 3D and 4D NMR. The only difference, naturally, is the additional dimensions. By the time multiple experiments have been carried out, information regarding proximity of nuclei, the types of amino acid associated with each nuclei, and secondary structure has been amassed, and by carefully piecing all the data together, a 3D structure of a given protein can be constructed.
Other Applications of 2D NMR
2D NMR has many more applications beyond protein NMR, including characterization of pharmaceuticals, temperature dependence of carbohydrate conformations, and metabolomics, to just name a few. For more information on these applications and the 2D NMR techniques that are used in them, please see the “Further Reading” section.
References
- Aue, W., E. Bartholdi, R.R. Ernst, Two‐dimensional spectroscopy. Application to nuclear magnetic resonance. The Journal of Chemical Physics, 1976. 64: p. 2229.
- Gomathi, L., Elucidation of secondary structures of peptides using high resolution NMR. Current Science, 1996. 71(7): p. 553.
- Levitt, M.H., Spin Dynamics: Basics of Nuclear Magnetic Resonance. 2008: Wiley
- Jacobsen, N.A., NMR Spectroscopy Explained: Simplified Theory, Applications and Examples for Organic Chemistry and Structural Biology. 2007: Wiley. 668.
- Ames, J.B., Hamasaki, N., Molchanova, T., Structure and calcium-binding studies of a recoverin mutant (E85Q) in an allosteric intermediate state. Biochemistry, 2002. 41(18): p. 5776. DOI: 10.1021/bi012153k
- Clore, G.G., Angela M., Determining structures of large proteins and protein complexes by NMR. Biological Magnetic Resonance, 1998. 16.
Outside Links
- http://en.Wikipedia.org/wiki/Two-dim...e_spectroscopy
- triton.iqfr.csic.es/guide/eNM...nv/hsqc2d.html
- www.bioc.aecom.yu.edu/labs/gi...rator_2012.pdf
- www.chem.queensu.ca/facilitie.../hmqc.htm#hsqc
Problems
- What is the effect of the 90° pulse on the bulk magnetization of a sample?
- If a 90° pulse for a give sample is 4 fs long, how long is a 180° pulse on the same sample?
- The magnetic effect of which type of particle must be removed from an NMR experiment in order to observe an NOE?
Solutions: 1) a 90o pulse moves the bulk magnetization into the transverse plane 2) 8 fs 3) electrons
Further Reading
- Ludwig, C., Viant, Mark R., Two-dimensional J-resolved NMR spectroscopy: review of a key methodology in the metabolomics toobox. Phytochemical Analysis, 2010. 21(1): p. 22-32. DOI: 10.1002/pca.1186
- Brown, S.P., Applications of high-resolution 1H solid-state NMR. Solida State Nuclear Magnetic Resonance, 2012. 41: p. 1-27. DOI: 10.1016/j.ssnmr.2011.11.006
- Shrot, Y.F., Lucio, Ghost-peak suppression in ultrafast two-dimensional NMR. Journal of Magnetic Resonance, 2003. 164(2): p. 351-357. DOI: 10.1016/S1090-7807(03)00177-0

