EPR - Theory
- Page ID
- 1794
Electron Paramagnetic Resonance (EPR), also called Electron Spin Resonance (ESR), is a branch of magnetic resonance spectroscopy which utilizes microwave radiation to probe species with unpaired electrons, such as radicals, radical cations, and triplets in the presence of an externally applied static magnetic field. In many ways, the physical properties for the basic EPR theory and methods are analogous to Nuclear Magnetic Resonance (NMR). The most obvious difference is that the direct probing of electron spin properties in EPR is opposed to nuclear spins in NMR. Although limited to substances with unpaired electron spins, EPR spectroscopy has a variety of applications, from studying the kinetics and mechanisms of highly reactive radical intermediates to obtaining information about the interactions between paramagnetic metal clusters in biological enzymes. EPR can even be used to study the materials with conducting electrons in the semiconductor industry.
Historical Development of EPR
In 1896, the line splitting in optical spectra in a static magnetic field was first found by a Dutch physicist Zeeman. In 1920s, Stern and Gerlach sent a beam of silver atoms through an inhomogeneous magnetic field and the beam splits into two distinct parts, indicating the intrinsic angular momentum of electrons and atoms. Then Uhlenbeck and Goudsmit proposed that the electrons have an angular momentum. In 1938, Isidor Rabi measured the magnetic resonance absorption of lithium chloride molecules, which means he could measure different resonances to get more detailed information about molecular structure. After World War II, microwave instrumentation’s widespread availability sped up the development of electron paramagnetic resonance (EPR). The first observation of a magnetic resonance signal was detected by a Soviet physicist Zavoisky in several salts, including hydrous copper chloride, copper sulfate and manganese sulfate in 1944. Later the Oxford group proposed the basic theory of magnetic resonance. Contributed by many researchers, such as Cummerow & Halliday and Bagguley & Griffiths, EPR was extensively studied. Between 1960 and 1980, continuous wave (CW) EPR was developed and pulsed EPR was mainly studied in Bell laboratories. EPR was usually applied for organic free radicals. In the 1980s, the first commercial pulsed EPR spectrometer appeared in the market and was then extensively used for biological, medical field, active oxygen and so on. Nowadays, EPR has become a versatile and standard research tool.
EPR is fundamentally similar to the more widely familiar method of NMR spectroscopy, with several important distinctions. While both spectroscopies deal with the interaction of electromagnetic radiation with magnetic moments of particles, there are many differences between the two spectroscopies:
- EPR focuses on the interactions between an external magnetic field and the unpaired electrons of whatever system it is localized to, as opposed to the nuclei of individual atoms.
- The electromagnetic radiation used in NMR typically is confined to the radio frequency range between 300 and 1000 MHz, whereas EPR is typically performed using microwaves in the 3 - 400 GHz range.
- In EPR, the frequency is typically held constant, while the magnetic field strength is varied. This is the reverse of how NMR experiments are typically performed, where the magnetic field is held constant while the radio frequency is varied.
- Due to the short relaxation times of electron spins in comparison to nuclei, EPR experiments must often be performed at very low temperatures, often below 10 K, and sometimes as low as 2 K. This typically requires the use of liquid helium as a coolant.
- EPR spectroscopy is inherently roughly 1,000 times more sensitive than NMR spectroscopy due to the higher frequency of electromagnetic radiation used in EPR in comparison to NMR.
It should be noted that advanced pulsed EPR methods are used to directly investigate specific couplings between paramagnetic spin systems and specific magnetic nuclei. The most widely application is Electron Nuclear Double Resonance (ENDOR). In this method of EPR spectroscopy, both microwave and radio frequencies are used to perturb the spins of electrons and nuclei simultaneously in order to determine very specific couplings that are not attainable through traditional continuous wave methods.
Origin of the EPR Signal
An electron is a negatively charged particle with certain mass, it mainly has two kinds of movements. The first one is spinning around the nucleus, which brings orbital magnetic moment. The other is "spinning" around its own axis, which brings spin magnetic moment. Magnetic moment of the molecule is primarily contributed by unpaired electron's spin magnetic moment.
\[M_{S}=\sqrt{S(S+1)} \dfrac{h}{2\pi } \label{1}\]
- \(M_S\) is the total spin angular moment,
- \(S\) is the spin quantum number and
- \(h\) is Planck’s constant.
In the z direction, the component of the total spin angular moment can only assume two values:
\[M_{S_{Z}}=m_{S}\cdot \dfrac{h}{2\pi } \label{2}\]
The term ms have (2S + 1) different values: +S, (S − 1), (S − 2),.....-S. For single unpaired electron, only two possible values for ms are +1/2 and −1/2.
The magnetic moment, μe is directly proportional to the spin angular momentum and one may therefore write
\[\mu _{e}=-g_{e}\mu _{B}M_{S} \label{3}\]
The appearance of negative sign due to the fact that the magnetic mom entum of electron is collinear, but antiparallel to the spin itself. The term (geμB) is the magnetogyric ratio. The Bohr magneton, μB, is the magnetic moment for one unit of quantum mechanical angular momentum:
\[\mu_{B}=\dfrac{eh}{4\pi m_{e}} \label{4}\]
where e is the electron charge, me is the electron mass, the factor ge is known as the free electron g-factor with a value of 2.002 319 304 386 (one of the most accurately known physical constant). This magnetic moment interacts with the applied magnetic field. The interaction between the magnetic moment (μ) and the field (B) is described by
\[E=-\mu \cdot B\label{5}\]
For single unpaired electron, there will be two possible energy states, this effect is called Zeeman splitting.
\[E_{+\dfrac{1}{2}}=\dfrac{1}{2}g\mu _{B}B \label{6}\]
\[E_{-\dfrac{1}{2}}=-\dfrac{1}{2}g\mu _{B} B \label{7}\]
In the absence of external magnetic field,
\[E_{+1/2}=E{-1/2}=0\]
However, in the presence of external magnetic field (Figure 1), the difference between the two energy states can be written as
\[\Delta E=hv=g\mu _{B}B \label{8}\]
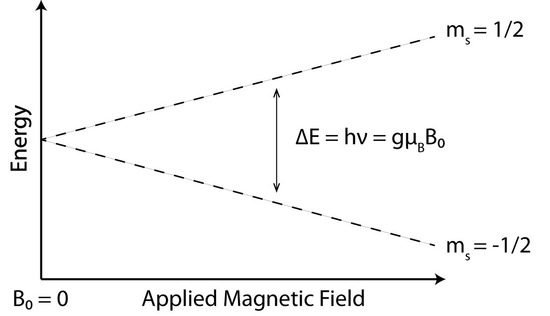
With the intensity of the applied magnetic field increasing, the energy difference between the energy levels widens until it matches with the microwave radiation, and results in absorption of photons. This is the fundamental basis for EPR spectroscopy. EPR spectrometers typically vary the magnetic field and hold the microwave frequency. EPR spectrometers are available in several frequency ranges, and X band is currently the most commonly used.
| Microwave band | Frequency/GHz | Wavelength/cm | B (electron)/Tesla |
|---|---|---|---|
| S | 3.0 | 10.0 | 0.107 |
| X | 9.5 | 3.15 | 0.339 |
| K | 23 | 1.30 | 0.82 |
| Q | 35 | 0.86 | 1.25 |
| W | 95 | 0.315 | 3.3 |
Energy Level Structure and the g-factor
EPR is often used to investigate systems in which electrons have both orbital and spin angular momentum, which necessitates the use of a scaling factor to account for the coupling between the two momenta. This factor is the g-factor, and it is roughly equivalent in utility how chemical shift is used in NMR. The g factor is associated with the quantum number J, the total angular momentum, where \(J=L+S\).
\[ g_J = \dfrac{J(J+1)(g_L+g_s)+(L(L+1)-S(S+1))(g_L-g_s)}{2J(J+1)} \label{9}\]
Here, \(g_L\) is the orbital g value and gs is the spin g value. For most spin systems with angular and spin magnetic momenta, it can be approximated that gL is exactly 1 and gs is exactly 2. T his equation reduces to what is called the Landé formula:
\[ g_J = \dfrac{3}{2}- \dfrac{L(L+1)-S(S+1))}{2J(J+1)} \label{10}\]
And the resultant electronic magnetic dipole is:
\[ \mu_{J} = -g_{J}\mu_{B}J \label{11}\]
In practice, these approximations do not always hold true, as there are many systems in which J-coupling does occur, especially in transition metal clusters where the unpaired spin is highly delocalized over several nuclei. But for the purposes of a elementary examination of EPR theory it is useful for the understanding of how the g factor is derived. In general this is simply referred to as the g-factor or the Landé g-factor.
The g-factor for a free electron with zero angular momentum still has a small quantum mechanical corrective \(g\) value, with g=2.0023193. In addition to considering the total magnetic dipole moment of a paramagnetic species, the g-value takes into account the local environment of the spin system. The existence of local magnetic fields produced by other paramagnetic species, electric quadrupoles, magnetic nuclei, ligand fields (especially in the case of transition metals) all can change the effective magnetic field that the electron experiences such that
\[ B_{eff} = B_{0}+B_{local} \label{12}\]
These local fields can either:
- be induced by the applied field, and hence have magnitude dependence on \(B_0\) o r are
- permanent and independent of \(B_0\) o ther than in orientation.
In the case of the first type, it is easiest to consider the effective field experienced by the electron as a function of the applied field, thus we can write:
\[ B_{eff} = B_{0}(1-\sigma)\label{13} \]
where \( \sigma \) is the shielding factor that results in decreasing or increasing the effective field. The g-factor must then be replaced by a variable g factor geff such that:
\[B_{eff}=B_{0}\cdot (\dfrac{g}{g_{eff}}) \label{14}\]
Many organic radicals and radical ions have unpaired electrons with \(L\) near zero, and the total angular momentum quantum number J becomes approximately S. As result, the g-values of these species are typically close to 2. In stark contrast, unpaired spins in transition metal ions or complexes typically have larger values of L and S, and their g values diverge from 2 accordingly.
After all of this, the energy levels that correspond to the spins in an applied magnetic field can now be written as:
\[E_{m_{s}}=m_{s}g_{e}\mu _{B}B_{0} \label{15}\]
And thus the energy difference associated with a transition is given as:
\[\Delta E_{m_{s}}=\Delta m_{s}g_{e}\mu _{B}B_{} \label{16}\]
Typically, EPR is performed perpendicular mode, where the magnetic field component of the microwave radiation is oriented perpendicular to the magnetic field created by the magnet. Here, the selection rule for allowed EPR transitions is \( \Delta m_{s} = \pm 1\), so the energy of the transition is simply:
(17) \[\Delta E_{m_{s}}=g_{e}\mu _{B}B_{} \label{17}\]
There is a method called Parallel Mode EPR in which the microwaves are applied parallel to the magnetic field, changing the selection rule to \(\Delta m_{s} = \pm 2\). This is more fully explained in the Parallel Mode EPR: Theory module.
Sensitivity
At the thermal equilibrium and external applied magnetic field, the spin population is split between the two Zeeman levels (Figure 1) according to the Maxwell–Boltzmann law. Absorption can occur as long as the number of particles in the lower state is greater than the number of particles in the upper state. At equilibrium, the ratio predicted by the Boltzmann distribution:
\[\dfrac{N_{upper}}{N_{lower}}=e^{\dfrac{-\Delta E}{k_BT}}=e^{-\dfrac{g\mu B}{k_BT}} \label{18}\]
with kB is the Boltzmann constant.
At regular temperatures and magnetic fields, the exponent is very small and the exponential can be accurately approximated by the expansion,
\[e^{–x} \approx 1 – x\]
Thus
\[\dfrac{N_{upper}}{N_{lower}}=1-\dfrac{g\mu B}{k_BT} \label{19}\]
At 298 K in a field of about 3000 G the distribution shows that Nupper /Nlower=0.9986, which means the difference between is Nupperand Nlower is very small. The populations of the two Zeeman levels are nearly the same, but the slight excess in the lower level gives rise to a net absorption.
\[N_{lower}-N_{upper}=N_{lower}\left [ 1-\left ( 1-\dfrac{g\mu B}{k_BT} \right ) \right ]=\dfrac{Ng\mu B}{2k_BT} \label{20}\]
This expression tells us that EPR sensitivity (net absorption) increases as temperature decreases and magnetic field strength increases, and magnetic field is proportional to microwave frequency. Theoretically speaking, the sensitivity of spectrometer with K-band or Q-band or W-band shoulder be greater than spectrometer with X-band. However, since the K-, Q- or W-band waveguides are smaller, samples are necessarily smaller, thus canceling the advantage of a more favorable Boltzmann factor.
Spin Operators and Hamiltonians
Any system which has discrete energy levels and is described by defined quantum numbers can be represented by an eigenvalue equation, such that if we define an operator (\(\hat{\Lambda }\) ) that is appropriate to the property being observed, the eigenfunction equation is:
\[\hat{\Lambda }{\psi }_k=\ {\lambda }_k{\psi }_k \label{21}\]
Here λk is an eigenvalue of a state “k” for which the eigenfunction is ψk. EPR is most concerned with the quantization of spin angular momentum, therefore, the operator must be defined is a spin operator that operated on a function that describes a spin state. In the case of a system with a total electron spin of S = ½, the two states are described by the quantum numbers Ms = +1/2 and Ms = -1/2, which measure the components Ms of angular momentum along the z-direction of the magnetic field. In most systems, it is convenient to treat the direction of the magnetic field as the z-direction, and thus the spin operator is denoted Ŝz, where Ŝ is the angular momentum operator. So, omitting the k index, the z-component of the angular momentum operator can be written as:
\[\hat{S_z}\phi_e=M_s\phi_e \label{22}\]
where ms is the eigenvalue of the operator Sz, and ϕe(Ms) is the corresponding eigenfunction. Adopting the α- notation for spin states, where α(e) = ϕe(Ms=+1/2) and β(e) = ϕe(Ms=-1/2), this expression can be written:
\[\hat{S_z}\alpha \left(e\right)=+\dfrac{1}{2}\alpha \left(e\right) \label{23}\]
\[\hat{S_z}\beta \left(e\right)=-\dfrac{1}{2}\beta \left(e\right) \label{24}\]
In a similar fashion, the eigenfunctions for the nuclear spin operator for a nucleus with spin = ½ can be written:
\[\hat{I_z}\alpha \left(n\right)=+\dfrac{1}{2}\alpha \left(n\right) \label{25}\]
\[\hat{I_z}\beta \left(n\right)=-\dfrac{1}{2}\beta \left(n\right) \label{26}\]
Written in the convenient Dirac notation, these expressions become:
\[\left.\hat{S_z}\right|\left.\alpha \left(e\right)\right\rangle =+\left.\left.\dfrac{1}{2}\right|\alpha \left(e\right)\right\rangle \label{27}\]
\[\left.\hat{S_z}\right|\left.\beta \left(e\right)\right\rangle =+\left.\left.\dfrac{1}{2}\right|\beta \left(e\right)\right\rangle \label{28}\]
and
\[\left.\hat{I_z}\right|\left.\alpha \left(n\right)\right\rangle =+\left.\left.\dfrac{1}{2}\right|\alpha \left(n\right)\right\rangle \label{29}\]
\[\left.\hat{I_z}\right|\left.\beta \left(n\right)\right\rangle =+\left.\left.\dfrac{1}{2}\right|\beta \left(n\right)\right\rangle \label{30}\]
Using the time-independent Schrödinger equation, we can define the energies associated with the systems described by these equations as such:
\[\left.\hat{{{\mathcal H}}_e}\right|\left.\phi_{ek}\right\rangle =\left.E_{ek}\right|\left.\phi_{ek}\right\rangle \label{31}\]
\[\left.\hat{{{\mathcal H}}_n}\right|\left.\phi_{nk}\right\rangle =\left.E_{nk}\right|\left.\phi_{nk}\right\rangle \label{32}\]
So that
\[\left.\hat{{{\mathcal H}}_e}\right|\left.\alpha (e)\right\rangle =\left.E_{\alpha (e)}\right|\left.\alpha (e)\right\rangle \label{33}\]
\[\left.\hat{{{\mathcal H}}_e}\right|\left.\beta (e)\right\rangle =\left.E_{\alpha (e)}\right|\left.\beta (e)\right\rangle \label{34}\]
\[\left.\hat{{{\mathcal H}}_n}\right|\left.\alpha (n)\right\rangle =\left.E_{\alpha (n)}\right|\left.\alpha (n)\right\rangle \label{35}\]
\[\left.\hat{{{\mathcal H}}_n}\right|\left.\beta (n)\right\rangle =\left.E_{\alpha (n)}\right|\left.\beta (n)\right\rangle \label{36}\]
Here Ĥ is the Hamiltonian operator and represents the operator for the total energy, and commutes with both I and S operators.
Electron/Nuclear Zeeman Interactions using Operators
Using the Hamiltonians derived in the last section, we can develop hamiltonians for the perturbed case in which an external magnetic field is introduced. For the simple case of the hydrogen atom with S=1/2 and I=1/2, interaction with a strong magnetic field oriented along the z-direction will be considered. Using the operator form, the Hamiltonian takes the form:
\[\ {\hat{H}}= -B\hat{\mu }_z \label{37}\]
Here, the electron magnetic moment operator μez is proportional to the electron spin operator. Likewise, the nuclear magnetic moment operator μnzis proportional to the nuclear spin operator Iz. Therefore,
\[ \ {\hat{\mu }}_{ez}=\ {\gamma }_e{\hat{S}}_zh=\ -g{\mu}_B{\hat{S}}_z \label{38}\]
\[ \ {\hat{\mu }}_{nz}=\ {\gamma }_n{\hat{I}}_zh=\ +g_n{\mu }_n{\hat{I}}_z \label{39}\]
Now the electron and nuclear spin Hamiltonians can be defined as:
\[\ {\hat{\mathcal H}}_e=\ g_e{\mu}_B\hat{S_z} \label{40}\]
\[\ {\hat{\mathcal H}}_n=\ -g_n{\mu }_n\hat{I_z} \label{41}\]
We now have a quantum mechanical framework for the energies of electronic and nuclear spin states that will be further useful in developing a description of the interactions between the magnetic moments of the two classes of particles.
Nuclear Hyperfine Structure
According to the figure 1, we should observe one spectra line in a paramagnetic molecule, but in reality, we usually observe more than one split line. The reason for that is hyperfine interactions, which results from interaction of the magnetic moment of the unpaired electron and the magnetic nuclei. The hyperfine patterns are highly valuable when it comes to determine the spatial structure of paramagnetic species and identify the paramagnetic species. As a result, nuclear spins act as probes which are sensitive to the magnetitude and direction of the field due to the unpaired electron.
In general, there are two kinds of hyperfine interactions between unpaired electron and the nucleus. The first is the interaction of two dipoles. We refer it as the anisotropic or dipolar hyperfine interaction, which is the interaction between electron spin magnetic moment and the nuclei magnetic moment, and it depends on the shape of electronic orbital and the average distance of electron and nucleus. This interaction can help us to determine the possible position of a paramagnetic species in a solid lattice.
The second interaction is known as the Fermi contact interaction, and only takes the electrons in s orbital into consideration, since p, d and f orbitals have nodal planes passing through the nucleus. We refer to this type of interaction as isotropic, which depends on the presence of a finite unpaired electron spin density at the position of the nucleus, not on the orientation of the paramagnetic species in the magnetic field.
\[A=-\dfrac{8}{3}\pi \left \langle \mu _{n}\cdot \mu _{e} \right \rangle\cdot \left | \psi \left ( 0 \right ) \right |^{2} \label{42}\]
A is the isotropic hyperfine coupling constant and is related to the unpaired spin density, μn is the nuclear magnetic moment, μe is the electron magnetic moment and Ψ(0) is the electron wavefunction at the nucleus. The Fermi contact interaction happens in s orbital when electron density is not zero. Thus nuclear hyperfine spectra not only includes the interaction of nuclei and their positions in the molecule but also the extent to which part or all of the molecule is free to reorientate itself according to the direction of the applied magnetic field.
Isotropic Hyperfine Interaction
In the case of one unpaired electron, the spin hamiltonian can be written as below for the isotropc part of nuclear hyperfine interaction.
\[H=H_{EZ}-H_{NZ}-H_{HFS} \label{43}\]
EZ means electron Zeeman, NZ means nuclear Zeeman and HFS represents hyperfine interaction. The equation can also be written as
\[\hat{H}=g\mu _{B}HS_{Z}-g_{N}\mu _{N}\cdot BI_{Z}+h\cdot S\cdot aI \label{44}\]
The term aS*I is introduced by Fermi contact interaction. I is the nucleus spin, H is the external field. Since μBis much larger than μN, the equation can take the form as:
\[\hat{H}=g\mu _{B}HS_{Z}+h\cdot S\cdot aI \label{45}\]
When one unpaired electron interacts with one nucleus, the number of EPR lines is 2I+1. When one unpaired electron interacts with N equivalent nuclei, the number of EPR lines is 2NI+1. When one electron interacts with nonequivalent nucleis (N1, N2.....), the numer of EPR lines is
\[\prod_{i=1}^{k}(2N_{i}I_{i}+1) \label{46}\]
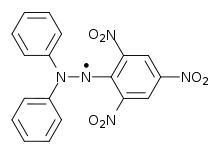
In the case of DPPH, I=1 and two nitrogen nucleui are equivalent. 2NI+1=5, we can get five lines: 1:2:3:2:1.
The table below shows the relative intensities of the lines according to unpaired electrons interacting with multiple equivalent nuclei.
|
Number of Equivalent Nuclei |
Relative Intensities |
|---|---|
|
1 |
1:1 |
|
2 |
1:2:1 |
|
3 |
1:3:3:1 |
|
4 |
1:4:6:4:1 |
|
5 |
1:5:10:10:5:1 |
|
6 |
1:6:15:20:15:6:1 |
We can observe that increasing number of nucleuses leads to the complexity of the spectrum, and spectral density depends on the number of nuclei as equation shown below:
\[Spectral density_{EPR}=\dfrac{\prod_{i=1}^{k}2N_{i}I_{i}+1}{\sum_{i=1}^{k}2\left | a_{i} \right |N_{i}I_{i}} \label{47}\]
\(a\) is the isotropic hyperfine coupling constant.
The g Anisotropy
From the below equation, we can calculate g in this way:
\[\Delta E=hv=g\mu _{B}B \label{48}\]
If the energy gap is not zero, g factor can be remembered as:
\[g\approx \dfrac{1}{14}\dfrac{\nu \left [ GHZ \right ]}{B\left [ T \right ]} \label{49}\]
The g factor is not necessarily isotropic and needs to be treated as a tensor g. For a free electron, g factor is close to 2. If electrons are in the atom, g factor is no longer 2, spin orbit coupling will shift g factor from 2. If the atom are placed at an electrostatic field of other atoms, the orbital energy level will also shift, and the g factor becomes anisotropic. The anisotropies lead to line broadening in isotropic ESR spectra. The Electron-Zeeman interaction depends on the absolute orientation of the molecule with respect to the external magnetic field. Anisotropic is very important for free electrons in non-symmetric orbitals (p,d).
In a more complex spin system, Hamiltonian is required to interpret as below:
\[\hat{H}_{s}=\mu _{B} \vec{B} \cdot g\cdot \hat{S}+\sum _{i} \vec{I}_{i}\cdot A_{i}\cdot \vec{S} \label{50}\]
g and Ai are 3*3 matrices representing the anisotropic Zeeman and nuclear hyperfine interactions, thus it is more accurate to describe g-factor as a tensor like:
\[g=\sqrt{g_{x}^{2}\cdot sin^{2}\alpha \cdot cos^{2}\beta +g_{y}^{2}\cdot sin^{2}\alpha \cdot cos^{2}\beta +g_{z}^{2}cos^{2}\alpha } \label{51}\]
Alpha and beta is the angle between magnetic field with respect to principle axis of g tensor. If gx=gy, it can be expressed as:
\[g=\sqrt{g_{x}^{2}\cdot sin^{2}\alpha +g_{z}^{2}cos^{2}\alpha } \label{52}\]
Thus, we can identify the g tensor by measuring the angular dependence in the above equation.
Spin Relaxation Mechanisms
The excess population of lower state over upper state for a single spin system is very small as we can calculate from the following example. With the temperature of 298K in a magnetic field of 3000G, Nupper /Nlower=0.9986, which means the populations of the two energy levels are almost equal, yet the slight excess in the lower level leads to energy absorption. In order to maintain a population excess in the lower level, the electrons from the upper level give up the hν energy to return to the lower level to satisfy the Maxwell–Boltzmann law. The process of this energy releasing is called spin relaxation process, of which there are two types, known as spin–lattice relaxation and spin–spin relaxation.
Spin-lattice relaxation
this implies interaction between the species with unpaired electrons, known as "spin system" and the surrounding molecules, known as "lattice". The energy is dissipated within the lattice as vibrational, rotational or translational energy. The spin lattice relaxation is characterized by a relaxation time T1e, which is the time for the spin system to lose 1/eth of its excess energy. Rapid dissipation of energy (short T1e) is essential if the population difference of the spin states is to be maintained. Slow spin-lattice relaxation, which is of frequent occurence in systems containing free radicals, especially at low temperatures, can cause saturation of the spin system. This means that the population difference of the upper and lower spin states approaches zero, and EPR signal ceases.
Spin-spin relaxation
Spin-spin relaxation or Cross relaxation, by which energy exchange happens between electrons in a higher energy spin state and nearby electrons or magnetic nuclei in a lower energy state, without transfering to the lattice. The spin–spin relaxation can be characterized by spin-spin relaxation time T2e.
When both spin–spin and spin–lattice relaxations contribute to the EPR signal, the resonance line width (ΔB) can be written as
\[\Delta B\propto \dfrac{1}{T_{1e}}+\dfrac{1}{T_{2e}} \label{53}\]
From the equation, we can tell that when T1e > T2e, ΔB depends primarily on spin–spin interactions. Decreasing the spin-spin distance, which is the spin concentration, T1e will become very short, approximately below roughly 10−7 sec, thus the spin-lattice relaxation will have a larger influence on the linewidth than spin-spin ralaxation. In some cases, the EPR lines are broadened beyond detection. When a spin system is weakly coupled to the lattice, the system tends to have a long T1e and electrons do not have time to return to the ground state, as a result the population difference of the two levels tends to approach zero and the intensity of the EPR signal decreases. This effect, known as saturation, can be avoided by exposing the sample to low intensity microwave radiation. Systems with shorter T1e are more difficult to saturate.
Parting Thoughts
Although EPR is limited to investigation of compounds and materials with unpaired electrons, it is undoubtedly the most direct and useful spectroscopic method for probing the properties of these specific systems. Another advantage is that sample preparation is simple and EPR does not cause destruction or activation in the sample. By probing the fundamental splitting of energy levels of spins with regard to their orientation in an external magnetic field, interactions between paramagnetic spin systems and their local environments can be detected. EPR spectra is highly sensitive to the local electonic structure, oxidation state and the proximity of magnetic nuclei to the system in question.
References
- Abragam, A. and Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Dover Publishing; 1986.
- Poole, C.P. Electron Spin Resonance; Interscience Publishers; 1967.
- Schweiger, A. & Jeschke, G. Principles of Pulse Electron Paramagnetic Resonance. Oxford University Press; 2001.
- Weil, J. A. & Bolton, J. R. Electron Paramagnetic Resonance Spectroscopy: Elementary Theory and Applications, Second Edition. Wiley-Interscience; 2007.
- Gale, Robert J ed. Spectroelectrochemistry: theory and practice. Plenum Press; 1988.
- Ayscough, Peter B. Electron Spin Resonance in Chemistry. Butler & Tanner Ltd; 1967.
Problems
- Why are microwaves necessary to study the electron spin resonances?
- What is the g-factor? What does it mean if the value is 2?
Answer
- EPR is targeted to unpaired electrons. Single unpaired electron behaves like a small magnetic bar when placed in a large maganetic field. It will orient itself parallel to the large magnetic field. At a particular magnetic field inensity, the microwave irradiation will induce unpaired electrons to orient against the large magnetic field. This effect will cause Zeeman splitting, when the energy difference between the lower and the higher energy level matches the microwave frequency. There will be absorption of energy, thus producing an EPR resonance, and detected by the spectrometer.
- As we have discussed before, g-factor can be calculated from measuring the magnetic field and frequency. g-factor is an effective Zeeman factor. For a free electron, isotropic ge = 2.0023193043617. It is predicted by quantum electrodynamics. This free electron has spin angular momentum but no orbital angular momentum. For electrons in an atom, g factor will shift from ge due to spin orbit coupling. thus g factor is the characteristic of different electronic structures.

