4.30: Modeling the Pi-electrons of Benzene as Particles on a Ring - Version 2

Wave-particle duality for massive objects as expressed by the de Broglie equation (λ = h/mv = h/p) is a foundational concept of quantum theory. Classical potential energy carries over to quantum mechanics unchanged, but classical kinetic energy is, as shown below, transformed into a quantum mechanical confinement energy by the de Broglie relation. Confined objects with wave properties are subject to interference which restricts the allowed values of λ, which in turn leads to energy quantization.

\[ T = \frac{p^2}{2m} \xrightarrow{p= \frac{h}{ \lambda}} \frac{h^2}{2m \lambda^2} \nonumber \]

A general one-dimensional function, \( \Psi (x) = \frac{1}{ \sqrt{2 \pi}} \text{exp} \left( i 2 \pi \frac{x}{ \lambda} \right)\), is used to represent the wave character of a particle on a ring (POR) where in order to avoid self-interference the head and tail of the wave function must match after one revolution.

\[ \begin{matrix} \Psi (x) = \Psi (x + C) & C = 2 \pi R \end{matrix} \nonumber \]

This requirement restricts the allowed values of the wavelength and leads to a manifold of quantized energies as is now demonstrated. The structure of the manifold of allowed energies depends on the nature of the confinement, each problem gives a characteristic energy manifold. For the particle on a ring we find,

\[ \frac{1}{ \sqrt{2 \pi}} \text{exp} \left( i 2 \pi \frac{x}{ \lambda} \right) = \frac{1}{ \sqrt{2 \pi }} \text{exp} \left( i 2 \pi \frac{x+C}{ \lambda} \right) = \frac{1}{ \sqrt{2 \pi}} \text{exp} \left( i 2 \pi \frac{x}{ \lambda} \right) \frac{1}{ \sqrt{2 \pi}} \text{exp} \left( i 2 \pi \frac{C}{ \lambda} \right) \nonumber \]

\[ \begin{matrix} \text{It follows that} & \frac{1}{ \sqrt{2 \pi}} \text{exp} \left( i 2 \pi \frac{C}{ \lambda} \right) = 1 & \text{which requires} & \lambda = \frac{C}{n} & \text{where n} = 0,~ \pm1,~ \pm 2 ...\end{matrix} \nonumber \]

Substitution of this restriction for λ into the quantum expression for kinetic energy yields an equation for the allowed energy states in terms of Planck's constant, the particle mass, the ring circumference and the quantum number, n.

\[ T = \frac{h^2}{2m \lambda^2} \text{substitute,}~ \lambda = \frac{C}{n} \rightarrow T = \frac{h^2 n^2}{2 C^2 m} \nonumber \]

An obvious POR application is to treat the π-electrons of benzene as particles on a ring. The energy level diagram is constructed using the above energy expression and the allowed values for the quantum number, n. Then the energy level diagram is populated with six π-electrons using the aufbau principle and the Pauli exclusion principle.

The validity of the model is tested by calculating the wavelength of the photon required for the HOMO-LUMO transition. The average c-c bond length in benzene is 140 pm, so the ring circumference is approximated as 6x140 pm. As shown below the photon wavelength required for the HOMO-LUMO transition is 194 nm, a value that might be described as "in the ball park."

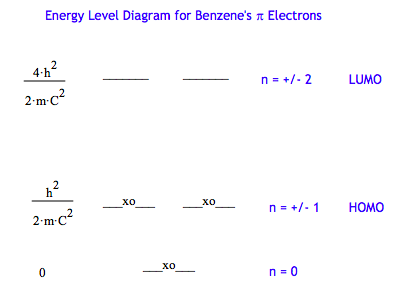
Energy conservation for the HOMO-LUMO transition requires:

\[ \frac{n_i^2 h^2}{2m_eC^2} + \frac{hc}{ \lambda} = \frac{n_f^2 h^2}{2m_eC^2} \nonumber \]

Fundamental constants and conversion factors:

\[ \begin{matrix} pm = 10^{-12}m & aJ = 10^{-18} J \end{matrix} \nonumber \]

\[ \begin{matrix} h = 6.626-755 (10^{-34} \text{joule sec} & c = 2.99792458 (10^8) \frac{m}{sec} & m_e = 9.1093897 (10^{-31}) kg \end{matrix} \nonumber \]

Calculate the photon wavelength for the HOMO-LUMO electronic transition.

\[ \begin{matrix} \text{HOMO:} & n_i = 1 & \text{LUMO:} & n_f = 2 & \text{Benzene circumference:} & C = 6(140) pm \end{matrix} \nonumber \]

\[ \begin{array}{c|c} \lambda = \frac{n_i^2 h^2}{2 m_e C^2} + \frac{hc}{ \lambda} = \frac{n_f^2 h^2}{2 m_e C^2} & _{ \text{solve, } \lambda}^{ \text{float, 3}} \rightarrow \frac{1.94e-7 \text{kg m}^3}{ \text{joule sec}^2 } ~ \lambda = 194 nm \end{array} \nonumber \]