Skip to main content
Chemistry LibreTexts

4.18: Analysis of the Vibrational and Electronic Spectrum of Benzene

  1. Last updated
  2. Save as PDF
  • Page ID
    150736

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    This tutorial deals with the interpretation of the vibrational and electronic spectra of benzene using group theory.

    Analysis of the Vibrational Spectrum

    The vibrational analysis uses the method of unmoved atoms (uma). The number of unmoved atoms for each symmetry operation is stored in a vector, Γuma. This is converted into a reducible representation (Γvib) for the vibrational degrees of freedom in several steps as is shown below. Next the irreducible representations that contribute to Γvib is determined.

    \[ \begin{matrix} D6h = \begin{pmatrix} 1 & 2 & 2 & 1 & 3 & 3 & 1 & 2 & 2 & 1 & 3 & 3 \end{pmatrix} & D6h = D6h^T & h = \sum D6h & h =24 \end{matrix} \nonumber \]

    \[ \begin{matrix} \begin{array} E & & E & C_6 & C_3 & C_2 & C_2' & C_2" & i & S_{3} & S_{6} & \sigma_h & \sigma_d & \sigma_v \end{array} & ~ \\ \text{CD6h} = \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & -1 & -1 & 1 & 1 & 1 & 1 & -1 & -1 \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & -1 & 1 & -1 & -1 & 1 & 1 & -1 & 1 & -1 & -1 & 1 \\ 2 & 1 & -1 & -2 & 0 & 0 & 2 & 1 & -1 & -2 & 0 & 0 \\ 2 & -1 & -1 & 2 & 0 & 0 & 2 & -1 & -1 & 2 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 & -1 \\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 & -1 & 1 & 1 \\ 1 & -1 & 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 & -1 & 1 \\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 & -1 & 1 & 1 & -1 \\ 2 & 1 & -1 & -2 & 0 & -0 & -2 & -1 & 1 & 2 & 0 & 0 \\ 2 & -1 & -1 & 2 & 0 & 0 & -2 & 1 & 1 & -2 & 0 & 0 \end{pmatrix} & \begin{array} \text{A1g: }x^2 + y^2 + z^2 \\ \text{A2g: Rz} \\ \text{B1g} \\ \text{B2g} \\ \text{E1g: (Rx, Ry), (xz, yz)} \\ \text{E2g: }(x^2 - y^2,~xy) \\ \text{A1u:} \\ \text{A2u: z} \\ \text{B1u:} \\ \text{B2u:} \\ \text{E1u: (x, y)} \\ \text{E2u:} \end{array} & \Gamma_{uma} = \begin{pmatrix} 12 \\ 0 \\ 0 \\ 0 \\ 4 \\ 0 \\ 0 \\ 0 \\ 0 \\ 12 \\ 0 \\ 4 \end{pmatrix} \end{matrix} \nonumber \]

    \[ \begin{matrix} \Gamma_{trans} = (CD6h^T)^{<g>} + (CD6h^T)^{<11>} & \Gamma_{rot} = (CD6h^T)^{<2>} + (CD6h^T)^{<5>} & \Gamma_{tot} = \overrightarrow{( \Gamma_{uma} \Gamma_{trans})} \end{matrix} \nonumber \]

    \[ \begin{matrix} \Gamma_{vib} = \Gamma_{rot} - \Gamma_{trans} - \Gamma_{rot} & i = 1 .. 12 & \text{Vib}_i = \frac{ \sum \overrightarrow{ \left[ D6h (CD6h^T )^{ <i>} \Gamma_{vib} \right] }}{h} \end{matrix} \nonumber \]

    \[ \text{Vib}^T = \begin{pmatrix} 2 & 1 & 0 & 2 & 1 & 4 & 0 & 1 & 2 & 2 & 3 & 2 \end{pmatrix} \nonumber \]

    \[ \Gamma_{vib} = 2A_{1g} + A_{2g} + 2B_{2g} + E_{1g} + 4E_{2g} + A_{2u} + 2B_{1u} + 1B_{2u} + 3E_{1u} + 2E_{2u} \nonumber \]

    The symmetry of the vibrational modes and their IR and Raman activity are given below:

    IR active: A2u and 3E1u

    Raman active: 2A1g, E1g, and 4E2g

    IR active modes are observed at 675, 1035, 1479, and 3036 cm-1, which is consistent with the above analysis. The Raman spectrum is not as clearly resolved.

    Analysis of the Electronic Spectrum

    The electronic spectrum to be analyzed (see below) is due to transitions involving benzene's π electrons. The symmetry of the relevant π−electron molecular orbitals is determined by examining how the π orbitals transform under the symmetry operations of the D6h group.

    \[ \begin{matrix} \Gamma_{ \pi} = \begin{pmatrix} 6 & 0 & 0 & -2 & 0 & 0 & 0 & -6 & 0 & 2 \end{pmatrix} & \Pi_i = \frac{ \sum \overrightarrow{ \left[ D6h (CD6h^T)^{<i>} \tau_{ \pi}^T \right]}}{h} \end{matrix} \nonumber \]

    \[ \begin{matrix} \Pi = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} & \begin{array} \text{A1g: }x^2 + y^2 + z^2 \\ \text{A2g: Rz} \\ \text{B1g} \\ \text{B2g} \\ \text{E1g: (Rx, Ry), (xz, yz)} \\ \text{E2g: }(x^2 - y^2,~xy) \\ \text{A1u:} \\ \text{A2u: z} \\ \text{B1u:} \\ \text{B2u:} \\ \text{E1u: (x, y)} \\ \text{E2u:} \end{array} \end{matrix} \nonumber \]

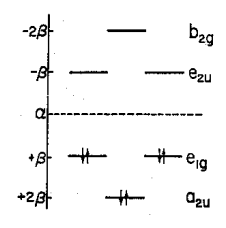
    Screen Shot 2019-05-16 at 1.05.46 PM.png

    The symmetry of the π-molecular orbitals is Γπ = B2g + E1g + A2u + E2u. The order of the levels from a Huckel calculation is as shown above: A2u, E1g, E2u, and B2g. The ground electronic state is A2u(2), E1g(4) and has A1g symmetry because the A2u and E1g orbitals are full. The first electronic excited state is A2u(2), E1g(3), E2u(1). This has the symmetry properties of E1g(1)E2u(1) which gives rise to the manifold of states: B1u, B2u, and E1u as is shown below.

    \[ \begin{matrix} X_i = \frac{ \sum \overrightarrow{ \left[ D6h (CD6h^T)^{<i>} (CD6h^T)^{<5>} (CD6h^T)^{<12>} \right]}}{h} & X^T = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 \end{pmatrix} \end{matrix} \nonumber \]

    The electronic energy level diagram consistent with this analysis is shown below. Note that the excited state splits into a set of singlet and triplet exited states. Transitions from the singlet ground state to the triplet excited states are formally forbidden.

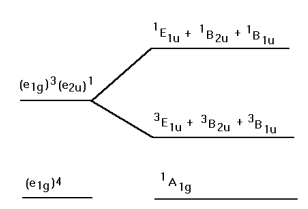
    Screen Shot 2019-05-16 at 1.10.37 PM.png

    For an electronic transition to be allowed the transition moment integral must be greater than zero.

    \[ \int \Psi_{ex} \mu_e \Psi_{eg} d \tau_e > 0 \nonumber \]

    Only the A1g ---> E1u transition is orbitally allowed as is shown below.

    \[ \begin{matrix} A_{1g} \rightarrow B_{1u} & \frac{ \sum \overrightarrow{ \left[ D6h (CD6h^T)^{<9>} \left[ (CD6h^T)^{<g>} + (CD6h^T)^{<11>} \right] (CD6h^T )^{<1>} \right]}}{h} = 0 \\ A_{1g} \rightarrow B_{2u} & \frac{ \sum \overrightarrow{ \left[ D6h (CD6h^T)^{<10>} \left[ (CD6h^T)^{<g>} + (CD6h^T)^{<11>} \right] (CD6h^T )^{<1>} \right]}}{h} = 0 \\ A_{1g} \rightarrow E_{1u} & \frac{ \sum \overrightarrow{ \left[ D6h (CD6h^T)^{<11>} \left[ (CD6h^T)^{<g>} + (CD6h^T)^{<11>} \right] (CD6h^T )^{<1>} \right]}}{h} = 0 \end{matrix} \nonumber \]

    Electronic transitions that are orbitally forbidden can occur if they are properly coupled to vibrational transitions. This occurs when the following integral is non-zero. These are called vibronic or vibrationally assisted electronic transitions.

    \[ \int \int \Psi_{ex} \Psi_{vx} \mu_e \Psi_{eg} \Psi_{vg} d \tau_e d \tau_v \nonumber \]

    The orbitally forbidden A1g --> B1u is vibronically assisted by B2g or E2g vibrations.

    \[ X_i = \frac{ \sum \overrightarrow{ \left[ D6h (CD6h^T)^{9} (CD6h^T)^{i} \left[ (CD6h^T)^{g} + (CD6h^T)^{11} \right] (CD6h^T)^{1} (CD6h^T)^{1} \right]}}{h} \\ X^T = \begin{pmatrix} 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} \nonumber \]

    The orbitally forbidden A1g --> B2u is vibronically assisted by B1g or E2g vibrations. However there is no B1g vibration.

    \[ X_i = \frac{ \sum \overrightarrow{ \left[ D6h (CD6h^T)^{10} (CD6h^T)^{i} \left[ (CD6h^T)^{g} + (CD6h^T)^{11} \right] (CD6h^T)^{1} (CD6h^T)^{1} \right]}}{h} \\ X^T = \begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} \nonumber \]

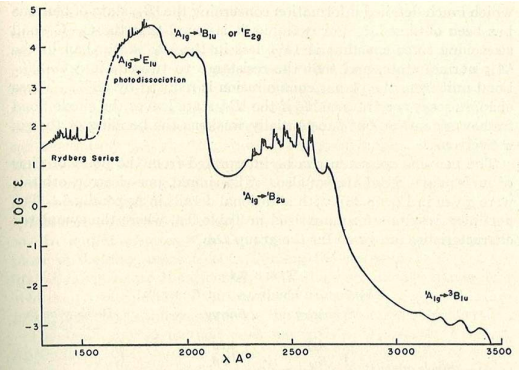
    Screen Shot 2019-05-16 at 1.19.44 PM.png

    The fully allowed A1g ---> E1u transition is assigned to the most intense transition which occurs at 180 nm. The vibronically assisted A1g --> B1u and A1g --> B2u transitions are assigned to the less intense bands at 200 and 260 nm, respectively. The spin-forbidden 1 A1g --> 3 B1u is assigned to the lowest energy and lowest intensity transition at 340 nm.

    This page titled 4.18: Analysis of the Vibrational and Electronic Spectrum of Benzene is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Frank Rioux via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.