4.17: Quantum Jumps for an Electron on a Ring

In spite of Max Born's warning, we are going to present a simple model for a quantum jump that is based on visualization.

This tutorial deals with the quantum mechanical particle (quon to use Nick Herbert's term) on a ring. Previously the behavior of the π-electrons of benzene were analyzed using this model. Links to the tutorials are provided below.

http://www.users.csbsju.edu/~frioux/...enzene-por.pdf

http://www.users.csbsju.edu/~frioux/...onsBenzene.pdf

In the absence of perturbations, such as oscillating electromagnetic fields, quantum systems are in the stationary states obtained from the solution of the time-independent Schrödinger equation. When a quantum system is subject to a perturbation such as an oscillating electromagnetic field it is forced into a time-dependent superposition of its stationary states.

\[ \Psi (q,~t) = \sum_n \left( \psi_n (q) \text{exp} \left( -i \frac{2 \pi E_n t}{h} \right) \right) \nonumber \]

For the system to absorb energy from the electromagnetic field and undergo a transition from one allowed energy state to another two conditions must be met. First, the photons of the electromagnetic field must satisfy the Bohr frequency condition by having an energy which equals the energy difference between the two states under consideration. Second, there must be a dipolar coupling between the electromagnetic field and the oscillating electron density of the system. This later criterion is, of course, the selection rule for the transition.

According to this model, when an electron on a ring is subjected to a electromagnetic perturbation, the electron responds by going into a state which is a linear superposition of the unperturbed stationary states. Assuming the Bohr frequency condition is satisfied for two states, if the square modulus, |Ψ(x,t)|², of the time-dependent wavefunction associated with this linear superposition exhibits an asymmetric fluctuating charge density (an oscillating dipole moment) on the ring, a coupling with the dipolar character of the electromagnetic field exists and a transition can occur. If the linear combination of states leads to a symmetric fluctuating charge density there is no coupling between the field and the electron density in the box and a transition is not possible.

The model is illustrated below for several possible transitions for an electron on a ring and the selection rule determined. Previously this model was used for the particle in a box and the harmonic oscillator. Links to these tutorials are provided below.

http://www.users.csbsju.edu/~frioux/q-jump/njump.pdf

http://www.users.csbsju.edu/~frioux/...mp/jumpsho.htm

http://www.users.csbsju.edu/~frioux/q-jump/p-jump.htm

Set up for graphics:

\[ \begin{matrix} \text{numpts} = 100 & i = 0 .. \text{numpts} & j = 0 .. \text{numpts} & \phi_i = \frac{2 \pi i}{ \text{numpts}} \\ x_{i,~j} = \cos ( \phi_i ) & y_{i,~j} = \sin ( \phi_i ) & z_{i,~j} = 0 & t = \frac{ \text{FRAME}}{3} \end{matrix} \nonumber \]

Form the time-dependent superposition of initial and final states:

\[ \begin{matrix} \text{Initial state:} & n_i = 0 & E_i = 2 n_i^2 \pi^2 & \text{Final state:} & n_f = 1 & E_f = 2 n_f^2 \pi^2 \end{matrix} \nonumber \]

\[ \Psi_{i,~j} = \frac{1}{2 \sqrt{ \pi}} \left( \left| \text{exp} (i n_1 \phi_i ) \text{exp} (-i E_i t) + \text{exp} ( i n_f \phi_i ) \text{exp} (-i E_ft ) \right| \right)^2 \nonumber \]

Select Animation and then Record from the Tools menu and follow instructions. Choose from 0 to 30 at 3 frames/sec for a reasonable animated display.

Before running the animation note that this superposition shows dipole character in that the electron density is a minimum at the opposite side of the ring at which it is a maximum. This dipole rotates around the ring during the animation, providing a mechanism for coupling with the electromagnetic field illuminating the particle on a ring, if the Bohr frequency condition is satisfied. Thus the transition from the n = 0 state to the n = 1 state is allowed. It is easy to show in this way that any transition for which ∆n = +/- 1 is allowed.

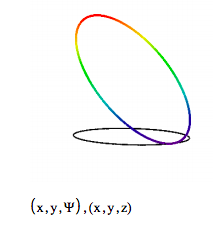
Now we look at a transition for which ∆n = 2. It is clear from the symmetry of the superposition wave function that the electron density distribution does not have dipole character, and, therefore, there is no mechanism for coupling with the electromagnetic field. It is easy to show that the same is true for ∆n = +/- 3, 4, etc.

\[ \begin{matrix} \text{Initial state:} & n_i = 1 & E_i = 2n_i^2 \pi^2 & \text{Final state:} & n_f = 3 & E_f = 2n_f^2 \pi^2 \end{matrix} \nonumber \]

\[ \Psi_{i,~j} = \frac{1}{2 \sqrt{ \pi}} \left( \left| \text{exp} (in_i \phi_i ) \text{exp} (-i E_i t) + \text{exp}(i n_f \phi_i ) \text{exp} (-i E_f t) \right| \right)^2 \nonumber \]

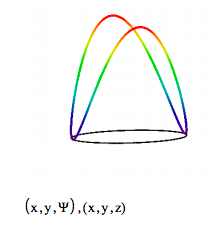
It is easy to show that while n = 1 to 2 and n = -1 to -2 transitions are allowed, the n = 1 to -2 and n = -1 to 2 transitions are forbidden, even though all of these transitions involve the same energy change.

Acknowledgement

The preparation of this tutorial and others on my page dealing with quantum jumps was stimulated by reading "Fluctuating Electric Dipoles and the Absorption of Light," by David R. McMillin [J. Chem. Ed. 55, 7 (1978)] .