8.52: Hardy's Paradox

Hardy's paradox is based on analysis of the double Mach-Zehnder interferometer shown below. A positron enters one interferometer and an electron the other. One arm of each interferometer intersect allowing for electron-positron interaction.

In the subsequent quantum mechanical analysis it will be shown that the paradox in Hardy's thought experiment is that it shows that the electron and positron have some probability of interacting without annihilation occurring.

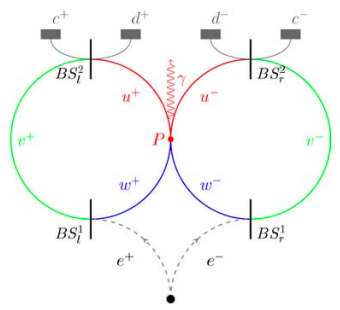
There are two 50-50 beam splitters in each interferometer. The probability amplitude for transmission is \( \frac{1}{ \sqrt{2}}\) and for reflection it is \( \frac{i}{ \sqrt{2}}\). By convention a 90 degree phase shift is assigned to reflection at the beam splitters.

Initially we ignore interaction at the intersection between the two interferometers. The initial state is |p>|e> represented by pe in Mathcad syntax - p represents the positron and e the electron. The rest of the terms are self-explanatory.

The evolution of the initial state is calculated below and we see that in the absence of interaction in the intersecting arms of the interferometers the electron and positron will be registered at their c-detectors. Recall that we calculate a probability amplitude and its absolute square gives the probability (|-1|² = 1).

\[ p~e~ \begin{array}{|l} \text{substitute, e} = \frac{1}{ \sqrt{2}} (v_e + i w_e) \\ \text{substitute, p} = \frac{1}{ \sqrt{2}} (v_p + i w_p) \\ \text{substitute, } v_p = \frac{1}{ \sqrt{2}} (i c_p + d_p) \\ \text{substitute, } w_p = \frac{1}{ \sqrt{2}} (c_p + i d_p) \\ \text{substitute, } w_e = \frac{1}{ \sqrt{2}} (c_e + i d_e) \\ \text{substitute, } v_e = \frac{1}{ \sqrt{2}} (i c_e + d_e) \end{array} \nonumber \]

Now we look at the situation immediately after the first set of beam splitters and explore the implication of interaction, or in this case electron-positron annihilation.

\[ p~e~ \begin{array}{|l} \text{substitute, e} = \frac{1}{ \sqrt{2}} (v_e + i w_e) \\ \text{substitute, p} = \frac{1}{ \sqrt{2}} (v_p + i w_p) \end{array} \rightarrow \frac{v_e v_p}{2} + \frac{v_p w_e i}{2} - \frac{w_e w_p}{2} + \frac{v_e w_p i}{2} \nonumber \]

The term w_ew_p gives the probability (25%) that the electron and positron will be in the intersecting arms of the interferometers and annihilate each other. Annihilation removes that amplitude term from further evolution. Replacing it with the symbol γ and calculating what happens at the second set of beam splitters yields the following result.

\[ p~e~ \begin{array}{|l} \text{substitute, } v_p = \frac{1}{ \sqrt{2}} (i c_p + d_p) \\ \text{substitute, } w_p = \frac{1}{ \sqrt{2}} (c_p + i d_p) \\ \text{substitute, } w_e = \frac{1}{ \sqrt{2}} (c_e + i d_e) \\ \text{substitute, } v_e = \frac{1}{ \sqrt{2}} (i c_e + d_e) \end{array} \rightarrow - \frac{ \gamma}{2} - \frac{3 c_e c_p}{4} + \frac{c_p d_e i}{4} - \frac{d_e d_p}{4} + \frac{c_e d_p i}{4} \nonumber \]

This calculation reveals the paradox. Earlier it was shown that in the absence of interaction ce and cp should fire simultaneously 100% of the time. Now, with interaction/annihilation, that drops to a probability of 9/16 and a photon detected 25% of the time. The bizarre part of the quantum mechanical calculation is in the next to the last term (d_ed_p/4) above. For both d detectors to fire requires the amplitude before the second set of beam splitters to be w_ew_p, as shown by the next to the last term on the right below.

\[ \frac{1}{2} w_ew_p~ \begin{array}{|l} \text{substitute, } w_e = \frac{1}{ \sqrt{2}} (c_e + i d_e) \\ \text{substitute, } w_p = \frac{1}{ \sqrt{2}} (c_p + i d_p) \end{array} \rightarrow -\frac{c_e c_p}{4} + \frac{c_p d_e i}{4} - \frac{d_e d_p}{4} + \frac{c_e d_p i}{4} \nonumber \]

But this amplitude should lead to annihilation. So quantum theory appears to permit a positron/electron interaction that does not lead to annihilation with a probability of 1/16.

The Appendix shows how to carry out the analysis using tensor algebra.

Appendix

The motion of the positron and electron to the left and right is represented by the following orthonormal vectors.

\[ \begin{matrix} L = \begin{pmatrix} 1 \\ 0 \end{pmatrix} & R = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{matrix} \nonumber \]

Initially the positron moves to the left and the electron to the right, giving the following initial state in tensor format.

\[ \text{p e} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \nonumber \]

The beam splitters and mirrors are represented by 2x2 matrices. The mirrors are implied in the above figure by the change in direction between the two beam splitters.

Beam splitter:

\[ \text{BS} = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \nonumber \]

Mirror:

\[ \text{M} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \nonumber \]

The four output states are calculated in tensor format using motional basis vectors, |L> and |R>.

\[ \begin{matrix} c_p d_e = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} & c_p c_e = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} & d_p d_e = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} & d_p c_e = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} & \end{matrix} \nonumber \]

The operator representing the dual Mach-Zehnder interferometers is constructed by tensor multiplication of BS and M matrix operators.

\[ \text{DMZ} = \text{kronecker(BS, BS) kronecker(M, M) kronecker(BS, BS)} \nonumber \]

The following calculations show that, in the absence of positron-electron interaction only the c-detectors fire simultaneously.

\[ \begin{matrix} \left[ \left| \begin{pmatrix} 1 & 0 & 0 & 0 \end{pmatrix} \text{DMZ} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \right| \right]^2 = 0 & \left[ \left| \begin{pmatrix} 0 & 1 & 0 & 0 \end{pmatrix} \text{DMZ} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \right| \right]^2 = 1 \\ \left[ \left| \begin{pmatrix} 0 & 0 & 1 & 0 \end{pmatrix} \text{DMZ} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \right| \right]^2 = 0 & \left[ \left| \begin{pmatrix} 0 & 0 & 0 & 1 \end{pmatrix} \text{DMZ} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \right| \right]^2 = 0 \end{matrix} \nonumber \]

To complete the analysis in tensor format we look at the p-e state immediately after the first set of beam splitters.

\[ \text{kronecker(BS, BS)} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0.5i \\ 0.5 \\ -0.5 \\ 0.5i \end{pmatrix} \nonumber \]

\[ \frac{1}{2} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} i \\ 0 \end{pmatrix} + \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ i \end{pmatrix} \begin{pmatrix} i \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ i \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right] = \frac{1}{2} \left[ \begin{pmatrix} i \\ 0 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 0 \\ i \end{pmatrix} \right] = \frac{1}{2} \begin{pmatrix} i \\ 1 \\ -1 \\ i \end{pmatrix} \nonumber \]

The third position on the product vector is the probability amplitude that the positron is in the right arm of its interferometer and that the electron is in the left arm of its interferometer - the w arms in the figure above. If the positron-electron pair interact annihilation occurs and a photon is produced. That term, therefore, is set to zero and the state used for the remaining evolution is,

\[ \frac{1}{2} \begin{pmatrix} i \\ 1 \\ 0 \\ i \end{pmatrix} \nonumber \]

This state interacts with the remaining mirrors and beam splitters.

\[ \text{BSM} = \text{kronecker(BS, BS) kronecker(M, M)} \nonumber \]

The following output probability calculations are in exact agreement with the earlier calculations.

\[ \begin{matrix} \left[ \left| \begin{pmatrix} 1 & 0 & 0 & 0 \end{pmatrix} \text{BSM} \frac{1}{2} \begin{pmatrix} i \\ 1 \\ 0 \\ i \end{pmatrix} \right| \right]^2 = 0.0625 & \left[ \left| \begin{pmatrix} 0 & 1 & 0 & 0 \end{pmatrix} \text{BSM} \frac{1}{2} \begin{pmatrix} i \\ 1 \\ 0 \\ i \end{pmatrix} \right| \right]^2 = 0.5625 \\ \left[ \left| \begin{pmatrix} 0 & 0 & 1 & 0 \end{pmatrix} \text{BSM} \frac{1}{2} \begin{pmatrix} i \\ 1 \\ 0 \\ i \end{pmatrix} \right| \right]^2 = 0.0625 & \left[ \left| \begin{pmatrix} 0 & 0 & 0 & 1 \end{pmatrix} \text{BSM} \frac{1}{2} \begin{pmatrix} i \\ 1 \\ 0 \\ i \end{pmatrix} \right| \right]^2 = 0.0625 \end{matrix} \nonumber \]