8.35: Mermin's Version of Bohm's EPR Gedanken Experiment
- Page ID
- 143979
The purpose of this tutorial is to summarize a gedanken experiment that reveals a conflict between the predictions of local realism and quantum mechanics. The thought experiment was presented by N. David Mermin in the American Journal of Physics (October 1981, pp 941-943) and Physics Today (April 1985, pp 38-47).
A spin-1/2 pair is prepared in a singlet state and the individual particles travel in opposite directions to a pair of detectors which are set up to measure spin in three directions in x-z plane: along the z-axis, and angles of 120 and 240 degrees with respect to the z-axis. The detector settings are labeled 1, 2 and 3, respectively.
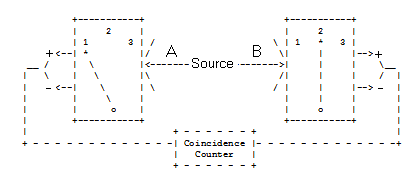
The switches on the detectors are set randomly so that all nine possible settings of the two detectors occur with equal frequency.
Local realism holds that objects have properties independent of measurement and that measurements at one location on a particle cannot influence measurements of another particle at another distant location even if the particles were created in the same event. Local realism maintains that the spin-1/2 particles carry instruction sets which dictate the results of subsequent measurements. That is, prior to measurement the particles are in an unknown but well-defined state.
The following table presents the experimental results expected on the basis of local realism. Singlet spin states have opposite spin values for each of the three measurement directions. For example, if A's spin state is (+-+), then B's spin state is (-+-). If A's detector is set to spin direction "1" and B's detector is set to spin direction "3" the measured result will be recorded as +-.
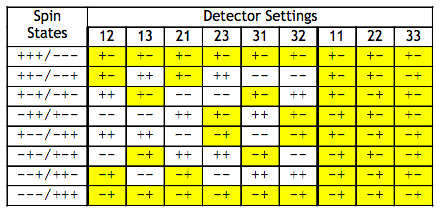
Note that there are eight spin states and nine possible detector settings, giving 72 possible measurement outcomes all of which are equally probable.
The table shows that the assumption that the singlet-state particles have well-defined spin states prior to measurement requires that the probability the detectors will register opposite spin values is 0.67 (48/72). If the detectors are set to the same direction, they always register different spin values (24/24), and if they are set to different directions the probability they will register different spin values is 0.50 (24/48).
We now show that quantum mechanics disagrees with the local realistic view just presented. The analysis that follows is based on material in chapters 6 and 11 of A. I. M. Rae's Quantum Mechanics.
The singlet state produced by the source is the following entangled superposition, where the arrows indicate the spin orientation for any direction in the x-z plane. As noted above the directions used here are 0, 120 and 240 degrees, relative to the z-axis.
\[ | \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ | \uparrow \rangle_1 \downarrow \rangle_2 - | \downarrow \rangle_1 | \uparrow \rangle_2 \right] \nonumber \]
The spin operator in the x-z plane is constructed from the Pauli spin operators in the x- and z-directions. φ is the angle of orientation of the measurement magnet with the z-axis. Note that the Pauli operators measure spin in units of h/4π. This provides for some mathematical clarity in the forthcoming analysis.
\[ \begin{matrix} \sigma_z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} & \sigma_x \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} & S( \varphi) = \cos (\varphi) \sigma_z + \sin ( \varphi) \sigma_x \rightarrow \begin{pmatrix} \cos \varphi & \sin \varphi \\ \sin \varphi & - \cos \varphi \end{pmatrix} \end{matrix} \nonumber \]
The spin-up and spin-down eigenvectors for this operator are as follow:
\[ \begin{matrix} \text{Eigenvalue +1} & \varphi_u (\varphi) = \begin{pmatrix} \cos \left( \frac{ \varphi}{2} \right) \\ \sin \left( \frac{ \varphi}{2} \right) \end{pmatrix} & S ( \varphi) \varphi_u ( \varphi) \text{simplify} \rightarrow \begin{pmatrix} \cos \left( \frac{ \varphi}{2} \right) \\ \sin \left( \frac{ \varphi}{2} \right) \end{pmatrix} \\ \text{Eigenvalue -1} & \varphi_d (\varphi) = \begin{pmatrix} - \sin \left( \frac{ \varphi}{2} \right) \\ \cos \left( \frac{ \varphi}{2} \right) \end{pmatrix} & S ( \varphi) \varphi_d ( \varphi) \text{simplify} \rightarrow \begin{pmatrix} \sin \left( \frac{ \varphi}{2} \right) \\ - \cos \left( \frac{ \varphi}{2} \right) \end{pmatrix} \end{matrix} \nonumber \]
Note that we get the expected eigenvectors for the z- and x-directions for angles of 0 and 90 degrees, respectively.
\[ \begin{matrix} \varphi_u (0) = \begin{pmatrix} 1 \\ 0 \end{pmatrix} & \varphi_d (0) = \begin{pmatrix} 0 \\ 1 \end{pmatrix} & \varphi_u \left( \frac{ \pi}{2} \right) = \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} & \varphi_d \left( \frac{ \pi}{2} \right) = \begin{pmatrix} -0.707 \\ 0.707 \end{pmatrix} \end{matrix} \nonumber \]
For spin measurements in which the detectors are set at the same angle quantum mechanics agrees with local realism that the detectors will register opposite spins. To illustrate what quantum mechanics predicts when the detectors are set at different angles we will consider a specific example. Suppose the particle at detector A is found to be spin-up in the z-direction, \( \begin{pmatrix} 1 \\ 0 \end{pmatrix}\). It follows from the singlet spin state that the particle at B is spin-down in the z-direction, \( \begin{pmatrix} 0 \\ 1 \end{pmatrix}\). But as shown below this state can be written as a superposition of φu and φd.
\[ \sin \left( \frac{ \varphi}{2} \right) \varphi_u ( \varphi) + \cos \left( \frac{ \varphi}{2} \right) \varphi_d (\varphi) \text{simplify} \rightarrow \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
The quantum mechanical prediction of the spin measurement at an angle φ on particle B is given by the squares of the coefficients of φu and φd. Therefore the probability that the measurement on particle B will be opposite of that on particle A is cos2(φ/2), which is 0.25 for angles of 120 and 240 degrees.
Thus over-all quantum mechanics predicts that opposite spins will be recorded [(1/3)100% + (2/3)25% ] 50% of the time, in sharp disagreement with the 67% calculated on the basis on local realism.
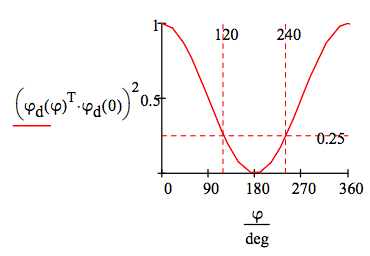
Next it is shown that the result of 25% is general for detector angle differences of 120 degrees (2π/3). First the 0-120 degree result is calculated using a different but equivalent method. The particle at detector A was found to be spin-up in the z-direction (φ = 0 deg) requiring that particle B is spin-down in the z-direction. The probability that particle B will be found spin-down when its detector is set to 120 deg is the square of the projection of φd(0) onto φd(2π/3). The state vectors are real so it is not necessary to square the absolute magnitude.
\[ \left( \varphi_d (120~ \text{deg})^T \varphi_d(0) \right)^2 = 0.25 \nonumber \]
This calculation is now repeated for the 30-150, 60-180, 90-210 and 120-240 detector orientations.
\[ \begin{matrix} \left( \varphi_d (150~ \text{deg})^T \varphi_d(30~ \text{deg}) \right)^2 = 0.25 & \left( \varphi_d (180~ \text{deg})^T \varphi_d(60~ \text{deg}) \right)^2 = 0.25 \\ \left( \varphi_d (210 ~\text{deg})^T \varphi_d(90~ \text{deg}) \right)^2 = 0.25 & \left( \varphi_d (120~ \text{deg})^T \varphi_d(120~ \text{deg}) \right)^2 = 0.25 \end{matrix} \nonumber \]
This graphic shows the probability calculation for all detector orientations.
Summary
Local realism maintains that objects have well-defined properties independent of observation, and that the acquisition of a definite value for a property by an object at B due to a measurement carried out on a distant object at A is "spooky action at a distance" and physically unintelligible and therefore impossible.
By contrast quantum theory teaches that quantum particles do not in general have well-defined properties independent of measurement, and that particles with a common origin are in an entangled state and therefore are not independent, no matter how far apart they may be. Together they are in a well-defined correlated state, but their individual properties are uncertain. When measurement determines the state of the particle at A, the correlated property of its distant partner at B becomes known instantaneously.

