8.26: Hardy's Paradox - An Algebraic Analysis

Hardy created a two-photon thought experiment for which a local hidden-variable (EPR) model for the photon states is not consistent with all the predictions of quantum theory.

A source emits two photons in the following entangled state, \( \Psi = \frac{2}{ \sqrt{3}} \left( H_A H_B - \frac{1}{2} H'_A H'_B \right)\), with the first photon traveling to Alice at a detector to the left of the source and the second to Bob at a detector on the right.

The following diagram shows the directions that linear polarization measurements will be made on the entangled two-photon system. The detectors can be set to measure in either the H-V or H'-V' basis.

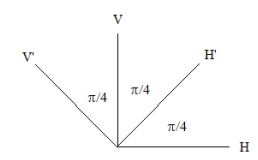
Alice and Bob record the results of a large number of independent, random polarization measurements on their photon pairs. The following table identifies all possible measurement outcomes. The probabilites of these outcomes are determined algebraically below.

\[ \begin{pmatrix} \text{V'V'} & \text{V'V} & \text{V'H'} & \text{V'H} \\ \text{VV'} & \text{VV} & \text{VH'} & \text{VH} \\ \text{H'V'} & \text{H'V} & \text{H'H'} & \text{H'H} \\ \text{HV'} & \text{HV} & \text{HH'} & \text{HH} \end{pmatrix} \nonumber \]

Alice and Bob both make H-V measurements:

\[ \Psi = \frac{2}{ \sqrt{3}} \left( H_A H_B - \frac{1}{2} H'_A H'_B \right) \begin{array}{|l} \text{substitute, } H'_A = \frac{1}{ \sqrt{2}} (H'_A - V'_A) \\ \text{substitute, } H'_B = \frac{1}{ \sqrt{2}} (H'_B - V'_B) \\ \text{simplify} \end{array} \rightarrow \Psi = \frac{\sqrt{3} V'_A V'_B}{3} - \frac{\sqrt{3} H'_B V'_A}{3} - \frac{\sqrt{3} H'_A V'_B}{3} \nonumber \]

Measurement probabilities: V'V' = V'H' = H'V' = 0.333

Alice and Bob both make H'-V' measurements:

\[ \Psi = \frac{2}{ \sqrt{3}} \left( H_A H_B - \frac{1}{2} H'_A H'_B \right) \begin{array}{|l} \text{substitute, } H'_A = \frac{1}{ \sqrt{2}} (H_A + V_A) \\ \text{substitute, } H_B = \frac{1}{ \sqrt{2}} (H_B - V_B) \\ \text{simplify} \end{array} \rightarrow \Psi = \frac{\sqrt{3} \left( H_A V_B - 3 H_A H_B + H_B V_A + V_A V_B \right)}{6} \nonumber \]

Measurement probabilities: HV = VH = VV = 0.083 HH = 0.75

Alice makes H-V measurements and Bob makes H'-V' measurements:

\[ \Psi = \frac{2}{ \sqrt{3}} \left( H_A H_B - \frac{1}{2} H'_A H'_B \right) \begin{array}{|l} \text{substitute, } H'_A = \frac{1}{ \sqrt{2}} (H_A + V_A) \\ \text{substitute, } H_B = \frac{1}{ \sqrt{2}} (H'_B - V'_B) \\ \text{simplify} \end{array} \rightarrow \Psi = \frac{\sqrt{6} H_A H'_B}{6} - \frac{\sqrt{6} H'_B V_A}{6} - \frac{\sqrt{6} H_A V'_B}{6} \nonumber \]

Measurement probabilities: HH' = VH' = 0.167 HV' = 0.667

Alice makes H'-V' measurements and Bob makes H-V measurements:

\[ \Psi = \frac{2}{ \sqrt{3}} \left( H_A H_B - \frac{1}{2} H'_A H'_B \right) \begin{array}{|l} \text{substitute, } H_A = \frac{1}{ \sqrt{2}} (H'_A + V'_A) \\ \text{substitute, } H'_B = \frac{1}{ \sqrt{2}} (H_B + V_B) \\ \text{simplify} \end{array} \rightarrow \Psi = \frac{\sqrt{6} H_B H'_A}{6} - \frac{\sqrt{6} H'_A V_B}{6} - \frac{\sqrt{6} H_B V'_A}{3} \nonumber \]

Measurement probabilities: H'H = H'V = 0.167 V'H = 0.667

The following measurement outcomes never occur: VV' = V'V = H'H' = 0

The results are collected in the following table.

\[ \begin{bmatrix} \left( \left| V'V'^T \Psi \right| \right)^2 & \left( \left| V'V^T \Psi \right| \right)^2 & \left( \left| V'H'^T \Psi \right| \right)^2 & \left( \left| V'H^T \Psi \right| \right)^2 \\ \left( \left| VV'^T \Psi \right| \right)^2 & \left( \left| VV^T \Psi \right| \right)^2 & \left( \left| VH'^T \Psi \right| \right)^2 & \left( \left| VH^T \Psi \right| \right)^2 \\ \left( \left| H'V'^T \Psi \right| \right)^2 & \left( \left| H'V^T \Psi \right| \right)^2 & \left( \left| H'H'^T \Psi \right| \right)^2 & \left( \left| H'H^T \Psi \right| \right)^2 \\ \left( \left| HV'^T \Psi \right| \right)^2 & \left( \left| HV^T \Psi \right| \right)^2 & \left( \left| HH'^T \Psi \right| \right)^2 & \left( \left| HH^T \Psi \right| \right)^2 \\ \end{bmatrix} = \begin{pmatrix} 0.333 & 0 & 0.333 & 0.667 \\ 0 & 0.083 & 0.167 & 0.083 \\ 0.333 & 0.167 & 0 & 0.167 \\ 0.667 & 0.083 & 0.167 & 0.75 \end{pmatrix} \nonumber \]

Hardy's paradox is revealed by concentrating on four entries in the table.

\[ \begin{pmatrix} \text{Alice} & \text{Bob} & \text{Result} \\ V & V' & \text{Never} \\ V' & V & \text{Never} \\ V & V & \text{Sometimes} \\ H' & H' & \text{Never} \end{pmatrix} \nonumber \]

In any run the detectors might be set to measure [H'-V']/[H-V] or [H-V]/[H'-V']. So if one photon triggers a [H-V] detector to register V, its partner must require a [H'-V'] detector to register H' according to the first two rows of the table above. According to the local hidden-variable model (EPR) this means H' is an element of reality.

It follows that any [H-V]/[H-V] run in which both detectors register V (probability 0.083) each photon must require a [H'-V'] detector to register H'. Therefore, if a [H'-V']/[H'-V'] run had been selected both detectors would have registered H'. However, given the initial photon state function the result H'H' should never be observed. In other words it is impossible to assign specific polarization states (instruction sets) to the photons prior to measurement that are in agreement with all quantum mechanical predictions for this thought experiment.

C. C. Gerry and K. M. Bruno, The Quantum Divide, Oxford U. P., 2013, pp. 124-29.