8.25: Lucien Hardy's Paradox as Presented by N. David Mermin

Hardy created a two-photon thought experiment for which a local hidden-variable (EPR) model for the photon states is not consistent with all the predictions of quantum theory.

A source emits two photons in the following entangled state, \( \Psi = \frac{2}{ \sqrt{3}} \left( H_A H_B - \frac{1}{2} H'_A H'_B \right)\), with the first photon traveling to Alice at a detector to the left of the source and the second to Bob at a detector on the right.

The following diagram shows the directions that linear polarization measurements will be made on the entangled two-photon system. The detectors can be set to measure in either the H-V or H'-V' basis.

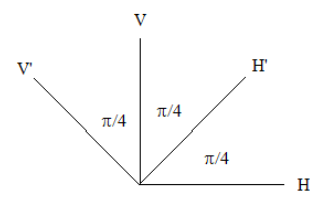
Definition of polarization eigenstates:

\[ \begin{matrix} H = \begin{pmatrix} 1 \\ 0 \end{pmatrix} & V = \begin{pmatrix} 0 \\ 1 \end{pmatrix} & H' = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} & V' = \frac{1}{ \sqrt{2}} \begin{pmatrix} -1 \\ 1 \end{pmatrix} \end{matrix} \nonumber \]

Ψ is expressed in tensor format:

\[ \begin{matrix} \Psi = \frac{2}{ \sqrt{3}} \left[ \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} - \frac{1}{4} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} \right] & \Psi = \begin{pmatrix} 0.866 \\ -0.289 \\ -0.289 \\ -0.289 \end{pmatrix} & \Psi^T \Psi = 1 \end{matrix} \nonumber \]

The first photon goes to Alice, the second to Bob. They record the results of a large number of independent, random polarization measurements on their photon pairs. They could for example enter their results in the following table which identifies all possible measurement outcomes.

\[ \begin{pmatrix} \text{V'V'} & \text{V'V} & \text{V'H'} & \text{V'H} \\ \text{VV'} & \text{VV} & \text{VH'} & \text{VH} \\ \text{H'V'} & \text{H'V} & \text{H'H'} & \text{H'H} \\ \text{HV'} & \text{HV} & \text{HH'} & \text{HH} \end{pmatrix} \nonumber \]

The next step is to calculate the probability that these observations will be made given Ψ as the initial state. To this end we form the product state vectors in tensor format using the definitions of H, V, H' and V' provided earlier.

\[ \begin{matrix} \text{V'V'} = \frac{1}{2} \begin{pmatrix} 1 \\ -1 \\ -1 \\ 1 \end{pmatrix} & \text{V'V} = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ -1 \\ 0 \\ 1 \end{pmatrix} & \text{V'H'} = \frac{1}{2} \begin{pmatrix} -1 \\ -1 \\ 1 \\ 1 \end{pmatrix} & \text{V'H} = \frac{1}{ \sqrt{2}} \begin{pmatrix} -1 \\ 0 \\ 1 \\ 0 \end{pmatrix} \\ \text{VV'} = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 0 \\ -1 \\ 1 \end{pmatrix} & \text{VV} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} & \text{VH'} = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 0 \\ 1 \\ 1 \end{pmatrix} & \text{VH} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \\ \text{H'V'} = \frac{1}{2} \begin{pmatrix} -1 \\ 1 \\ -1 \\ 1 \end{pmatrix} & \text{H'V} = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 1 \end{pmatrix} & \text{H'H'} = \frac{1}{2} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} & \text{H'H} = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \end{pmatrix} \\ \text{HV'} = \frac{1}{ \sqrt{2}} \begin{pmatrix} -1 \\ 1 \\ 0 \\ 0 \end{pmatrix} & \text{HV} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} & \text{HH'} = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \end{pmatrix} & \text{HH} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \end{matrix} \nonumber \]

Using these two-photon state functions we now calculate the probability of occurrence for each possible measurement outcome, as displayed in the following matrix.

\[ \begin{bmatrix} \left( \left| V'V'^T \Psi \right| \right)^2 & \left( \left| V'V^T \Psi \right| \right)^2 & \left( \left| V'H'^T \Psi \right| \right)^2 & \left( \left| V'H^T \Psi \right| \right)^2 \\ \left( \left| VV'^T \Psi \right| \right)^2 & \left( \left| VV^T \Psi \right| \right)^2 & \left( \left| VH'^T \Psi \right| \right)^2 & \left( \left| VH^T \Psi \right| \right)^2 \\ \left( \left| H'V'^T \Psi \right| \right)^2 & \left( \left| H'V^T \Psi \right| \right)^2 & \left( \left| H'H'^T \Psi \right| \right)^2 & \left( \left| H'H^T \Psi \right| \right)^2 \\ \left( \left| HV'^T \Psi \right| \right)^2 & \left( \left| HV^T \Psi \right| \right)^2 & \left( \left| HH'^T \Psi \right| \right)^2 & \left( \left| HH^T \Psi \right| \right)^2 \\ \end{bmatrix} = \begin{pmatrix} 0.333 & 0 & 0.333 & 0.667 \\ 0 & 0.083 & 0.167 & 0.083 \\ 0.333 & 0.167 & 0 & 0.167 \\ 0.667 & 0.083 & 0.167 & 0.75 \end{pmatrix} \nonumber \]

So, where's the paradox, where's the problem? The paradox/problem is revealed by concentrating on four entries in the matrix above.

\[ \begin{pmatrix} \text{Alice} & \text{Bob} & \text{Result} \\ V & V' & \text{Never} \\ V' & V & \text{Never} \\ V & V & \text{Sometimes} \\ H' & H' & \text{Never} \end{pmatrix} \nonumber \]

In any run the detectors might be set to measure [H'-V']/[H-V] or [H-V]/[H'-V']. So if one photon triggers a [H-V] detector to register V, its partner must require a [H'-V'] detector to register H' according to the first two rows of the matrix above. According to the local hidden-variable model (EPR) this means H' is an element of reality.

It follows that any [H-V]/[H-V] run in which both detectors register V (probability 0.083) each photon must require a [H'-V'] detector to register H'. Therefore, if a [H'-V']/[H'-V'] run had been selected both detectors would have registered H'.

However, given the initial photon state function the result H'H' should never be observed. In other words it is impossible to assign specific polarization states (instruction sets) to the photons prior to measurement that are in agreement with all quantum mechanical predictions for this thought experiment.

An algebraic analysis shows that destructive interference eliminates the H'H' term. It also gives the correct probabilities for V'V', V'H' and H'V' measurements. Algebraic analysis could be used to produce the entire measurement outcome matrix calculated above.

\[ \begin{matrix} \frac{2}{ \sqrt{3}} \left[ | H \rangle_A |H \rangle_B - \frac{1}{2} H' \rangle_A |H' \rangle_B \right] \\ \text{Substitute} \\ |H \rangle = \frac{1}{ \sqrt{2}} \left( |H' \rangle - |V' \rangle \right) \\ \downarrow \\ \frac{2}{ \sqrt{3}} \left[ \frac{1}{ \sqrt{2}} \left( |H' \rangle_A - |V' \rangle_B \right) \frac{1}{ \sqrt{2}} \left( |H' \rangle_A - |V' \rangle_B \right) - \frac{1}{2} |H' \rangle_A |H' \rangle_B \right] \\ \downarrow \\ \frac{1}{ \sqrt{3}} \left[ |V' \rangle_A |V' \rangle_B - |V' \rangle_A |H' \rangle_B - |H' \rangle_A |V' \rangle_B \right] \end{matrix} \nonumber \]

Sources:

Lucien Hardy, "Spooky Action at a Distance in Quantum Mechanics," Contemporary Physics 39, 419-429 (1998).

N. David Mermin, "Quantum Mysteries Refined," American Journal of Physics 62, 880-887 (1994). C. C. Gerry and K. M. Bruno, The Quantum Divide, Oxford U. P., 2013, pp. 124-29.