7.42: A Quantum Delayed-Choice Experiment
- Page ID
- 142668
This note presents a critique of "Entanglement-Enabled Delayed-Choice Experiment," F. Kaiser, et al. Science 338, 637 (2012). This experiment was also summarized in section 6.3 of Quantum Weirdness, by William Mullin, Oxford University Press, 2017.
A source, S, emits two photons in opposite directions on the x-axis in the following polarization state, where v and h represent vertical and horizontal polarization, respectively.
\[ | \Psi \rangle_{AB} \frac{1}{ \sqrt{2}} \left[ |xv \rangle_A |xv \rangle_B + |xh \rangle_A |xh \rangle_B \right] \nonumber \]
Photon B travels to the left to a polarizing beam splitter, PBS. Photon A travels to the right entering an interferometer whose elements are a beam splitter (BS), two mirrors (M), and a polarization-dependent beam splitter (PDBS).

The implementation of the PDBS is shown here.
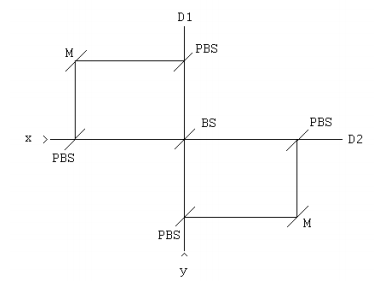
The operation of the optical elements are as follows. A mirror simply reflects the photon's direction of motion.
\[ M = |y \rangle \langle x | + |x \rangle \langle y | \nonumber \]
A 50-50 BS splits the photon beam into a superposition of motion in the x- and y-directions. By convention the reflected beam collects a pi/2 (i) phase shift relative to the transmitted beam.
\[ BS = \frac{|x \rangle + i | y \rangle}{ \sqrt{2}} \langle x | + \frac{i | x \rangle + | y \rangle}{ \sqrt{2}} \langle y | = \frac{1}{ \sqrt{2}} (|x \rangle \langle x | + i | y \rangle \langle x | + i | x \rangle \langle y | + |y \rangle \langle y |) \nonumber \]
A PBS transmits vertically polarized photons and reflects horizontally polarized photons.
\[ M = |y \rangle \langle x | + |x \rangle \langle y | \nonumber \]
A 50-50 BS splits the photon beam into a superposition of motion in the x- and y-directions. By convention the reflected beam collects a pi/2 (i) phase shift relative to the transmitted beam.
\[ BS = \frac{|x \rangle + i |y \rangle}{ \sqrt{2}} \rangle x| + \frac{i|x \rangle + |y \rangle}{ \sqrt{2}} \langle y | = \frac{1}{ \sqrt{2}} (|x \rangle \langle x | + i |y \rangle \langle x | + i | x \rangle \langle y | + |y \rangle \langle y| ) \nonumber \]
A PBS transmits vertically polarized photons and reflects horizontally polarized photons.
\[ PBS = |xv \rangle \langle xv | + |yh \rangle \langle xh | + |yv \rangle \langle yv | + |xh \rangle \langle yh | \nonumber \]
The PDBS uses an initial PBS to reflect horizontally polarized photons to a second PBS which reflects them to the detectors. Vertically polarized photons are transmitted by the first PBS to a BS which has the action shown above, after which they are transmitted to the detectors by the second PBS. PBS/PDBS blue/red color coding highlights the action of the central BS.
\[ PDPS = \frac{|xv \rangle + i | yv \rangle}{ \sqrt{2}} \langle xv | + |yh \rangle \langle xh + \frac{i|xv \rangle + |yv \rangle}{ \sqrt{2}} \langle yv| + |xh \rangle \langle yh| \nonumber \]
Given the state produced by the source, half the time a horizontal photon will enter the interferometer and half the time a vertical photon will enter. The following algebraic analysis shows the progress of the h- and v-polarized photons entering the interferometer. It is clear from this analysis that D1 will fire 25% of the time and D2 75% of the time.
\[ \begin{array}{c}
|xh \rangle & |xv \rangle \\
BS & BS \\
\frac{ |xh \rangle + i |yh \rangle}{ \sqrt{2}} & \frac{ |xv \rangle + i |yv \rangle}{ \sqrt{2}} \\
M & M \\
\frac{ |yh \rangle + i |xh \rangle}{ \sqrt{2}} & \frac{ |yv \rangle + i |xv \rangle}{ \sqrt{2}} \\
PDBS & PDBS \\
\frac{|D2 \rangle |h \rangle + i|D1 \rangle |h \rangle}{ \sqrt{2}} & \frac{1}{ \sqrt{2}} \left[ \frac{|D1 \rangle |v \rangle + i| D2 \rangle |v \rangle}{ \sqrt{2}} + \frac{i (i|D1 \rangle |v \rangle + D2 \rangle |v \rangle}{ \sqrt{2}} \right] \\
~ & \downarrow \\
~ & i|D2 \rangle |v \rangle \\
\end{array} \nonumber \]
This analysis suggests to some that inside the interferometer h-photons behave like particles and v-photons behave like waves. The argument for this view is that interference occurs at the PDBS for v-photons, but not for h-photons. However, in both cases the state illuminating the PDBS, highlighted in blue, is a superposition of the photon being in both arms of the interferometer. In my opinion this superposition implies delocalization which implies wavelike behavior. At the PDBS the h-photon superposition is reflected away from the central BS to D1 and D2, leading to the final superposition in the left-hand column above, which collapses on observation to either D1 or D2. The v-photon superposition is transmitted at the PDBS to the central BS allowing for destructive interference at D1 and constructive interference at D2 as is shown at the bottom of the right-hand column.
Those who interpret this experiment in terms of particle or wave behavior also invoke the concept of delayed-choice, claiming that if D2 fires we don't know for sure which behavior has occurred because both h and v photons can arrive there. They argue that until photon B has been observed at Dv or Dh, which by design can be long after photon A has exited the interferometer, the polarization of the photon detected at D2 is unknown and therefore so is whether particle or wave behavior has occurred. These analysts write the final two photon wavefunction as the following entangled superposition, where particle behavior is highlighted in red and wave behavior in blue.
\[ | \Psi \rangle_{final} = \frac{1}{ \sqrt{2}} \left( \left( \frac{|D2,h \rangle + i|D1,h \rangle}{ \sqrt{2}} \right)_A |Dh \rangle_B + i|D2,v \rangle_A |Dv \rangle_B \right) = \frac{1}{ \sqrt{2}} ( | Particle \rangle_A |Dh \rangle_B + | Wave \rangle_A |Dv \rangle_B ) \nonumber \]
For the reasons expressed above I do not find this interpretation convincing. We always observe particles (detectors click, photographic film is darkened, etc.), but we interpret what happened or predict what will happen by assuming wavelike behavior. In other words, objects governed by quantum mechanical principles (quons) exhibit both wave and particle properties in every experiment. To paraphrase Nick Herbert (Quantum Reality), particles are always detected, but the experimental results observed are the result of wavelike behavior. Bragg summarized wave-particle duality saying, "Everything in the future is a wave, everything in the past is a particle."

